Parametry, proszę o jak najszybszą pomoc :( milciak: Wiem, że dużo tego itp. ale nie było mnie długo w szkole i naprawdę nic nie ogarniam, a jutro sprawdzian więc proszę pomóżcie mi 1. a) Wyznacz wszystkie wartości parametru m, dla których równanie x² − 4mx − m³ + 6m + m − 2 = 0 B) to samo tylko, że jeszcze ma dwa różne pierwiastki takie, że (x₁ − x₂) ² < 8 (m+1) (nie mam pojęcia o robić po m² (m−2) − (m−2) >0 ) to zadanie już było na: https://matematykaszkolna.pl/strona/2998.html ale kompletnie nie wiem skąd tam się mnożenie wzięło i co dalej... 2. Oblicz wszystkie wartości parametru m, dla których równanie x² − (m+2)x + 4 + m =0 ma dwa pierwiastki rzeczywiste spełniające warunek x₁ ⁴ + x₂ ⁴ = 6 m² − 32m +12 3. Wskaż najmniejszą wartość funkcji f(x) = − 2x² − 3x+1 w przedziale <−3,0> Najpierw wydawało mi się, że podstawić −3 i 0 pod x f(x) = −8, f(x) = 1 ale to chyba zależy też od wierzchołka paraboli? 4. Suma najmniejszej i największej wartości funkcji f(x) = (x + 3) (x − 5) w przedziale <−2, 4> to tak samo jak z poprzednim najpierw pewnie f(x) = x² − 5x +3x − 15 = x² −2x − 15 ? 5. Δ= 4 k² − 4k wskaż zbiór rozwiązań, dla których równanie nie ma rozwiązań Δ<0 4 k² − 4k < 0 k² − k <0 k² − k =0 k² = k nie ma rozwiązań tylko dla k = −1 ? 6. Określ liczbę rozwiązań x² + (k+2) − k − 2 = 0 w zależności od wartości parametru k Proszę o chociaż coś, jutro mam z tego spr i naprawdę nic nie rozumiem

5-latek: https://matematykaszkolna.pl/forum/293954.html do zadania nr 4

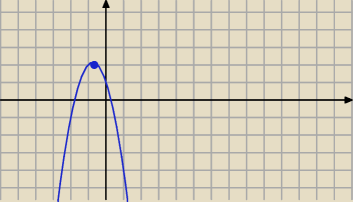
5-latek: W zadaniu nr 3 akuratnie nie zależy od wierzchołka paraboli bo masz znaleźćnajmniejsza wartość Ramiona paraboli masz w dol wiec w wierzchołku będzie wartość najwieksza Masz wykres tej funkcji (widzisz to ? czyli liczysz watosci na koncach przedzialu i wybierasz mniejsza wartość

milciak: czyli f(x) = −8 dzięki 3 i 4 już rozumiem ^^

milciak: a spróbujesz mi wytłumaczyć resztę? Było by super!

5-latek: ja już muszse isc spac bo jutro rano muszse wstać do pracy Popros może Pania Mile lub Pania Ete żeby CI wytłumaczyli Dobranoc

milciak: dzięki

olekturbo: 5 k²−k < 0 k(k−1)<0

milciak: k (k−1) = 0 k = 0 v k=1 ? coś mi nie pasuje, liczby chyba powinny być mniejsze od 0?

Mila: Oblicz wszystkie wartości parametru m, dla których równanie x² − (m+2)x + 4 + m =0 ma dwa pierwiastki rzeczywiste spełniające warunek x₁ ⁴ + x₂ 4 = 6 m² − 32m +12 1) równanie ma dwa pierwiastki ⇔ Δ>0 Δ=(m+2)²−4*(4+m)= m²+4m+4−16−4m Δ=m²−12>0⇔ (m−√12)*(m+√12)>0⇔ (m−2√3)*(m+2√3)>0 m<−2√3 lub m>2√3 2) teraz korzystamy z wzorów Viete'a

	−b
x1+x2=
	a

	c
x1*x2=
	a

x₁+x₂=m+2 x₁*x₂=m+4 x₁⁴+x₂⁴=(x₁²+x₂²)²−2*x₁²*x₂²= =[(x₁+x₂)²−2*x₁*x₂]²−2*(x₁*x₂)²= =[(m+2)²−2*(m+4)]²−2*(m+4)²= =[m²+4m+4−2m−8]²−2*(m²+8m+16)= =[m²+2m−4]²−2m²−16m−32= =(m²+2m−4)(m²+2m−4)−2m²−16m−32= =m⁴+2m³−4m²+2m³+4m²−8m−4m²−8m+16−2m²−16m−32= =m⁴+4m³−6m²−32m−16 I teraz porównanie: m⁴+4m³−6m²−32m−16=6 m² − 32m +12 m⁴+4m³−12m−28=0 Nie opuściłeś czegoś w drugim wyrażeniu może ma być : x₁ ⁴ + x₂ 4 = 4m³+6 m² − 32m +12

Martiminiano: Δ=4k²+4k Równanie kwadratowe nie ma rozwiązań, gdy Δ<0 4k²+4k<0 |:4 k(k+1)<0 k=0 v k=−1 a>0, więc ramiona skierowane do góry. Zatem Δ<0 dla k∊(−1;0)

olekturbo: Martiminiano u niego w przykładzie było 4k²−4k, dlatego k∊(0,1)

Martiminiano: 4. Suma najmniejszej i największej wartości funkcji f(x) = (x + 3) (x − 5) w przedziale <−2, 4> to tak samo jak z poprzednim x₁=−3 x₂=5

	x1+x2		−3+5
p=		=		=1
	2		2

a>0, p∊<−2;4>, więc wartość najmniejsza w tym przedziale przyjmowana jest dla wierzchołka f(p)=f(1)=(1+3)(1−5)=−16 f(−2)=(−2+3)(−2−5)=−7 f(4)=(4+3)(4−5)=−7 Wartość największa w tym przedziale wynosi −7 f_min+f_max=−16+(−7)=−23

Martiminiano: W porządku, przepraszam, źle spojrzałem.

Martiminiano: Sprawdź czy nie opuściłeś czegoś w 6.

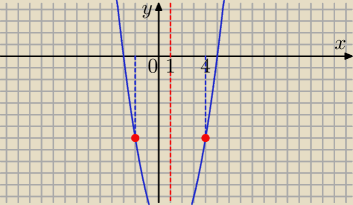
Mila: 4)Suma najmniejszej i największej wartości funkcji f(x) = (x + 3) (x − 5) w przedziale <−2, 4> miejsca zerowe: x₁=−3 x₂=5 Parabola skierowana do góry.

	x1+x2		−3+5
xw=		=		=1∊<−2,4>
	2		2

Zatem najmniejsza wartośc funkcji to f(1)=(1+3)*(1−5)=4*(−4)=−16 najwiekszej wartości szukamy na końcach przedziału: f(−2)=(−2+3)*(−2−5)=1*(−7)=−7 f(4)=(4+3)*(4−5)=7*(−1)=−7 −7+(−16)=−23

milciak: tak opuściłam, a skąd wiadomo w którą stronę będzie "roztwarty dziubek" po wyliczeniu pierwiastków m<−2{3} m> 2{3}? Tak przepraszam w 6: x² + (k+2) x − k −2 = 0

Martiminiano: Wskaż najmniejszą wartość funkcji f(x) =−2x²−3x+1 w przedziale <−3,0>

	−b		3		3
p=		=		=−		∊<−3,0> , ale a<0, więc w wierzchołku funkcja przyjmuje wartość
	2a		−4		4

największą f(−3)=−8=f_min f(0)=1 Teraz patrzę, że z rozpędu zrobiłem zadania które już były

milciak: Haha zawsze można jeszcze raz zobaczyć

Martiminiano: x²+(k+2)x−k−2=0 Δ=(k+2)²−4(−k−2)=k²+4k+4+4k+8=k²+8k+12=(k+2)(k+6) Dla k=−2 i dla k=−6 równanie posiada jedno rozwiązanie, bo Δ=0 Dla k∊(−∞;−6)∪(−2;+∞) równanie posiada dwa rozwiązania, bo Δ>0 Dla k∊(−6;−2) równanie nie posiada rozwiązań, bo Δ<0

Martiminiano: Czyli jeszcze tylko zadanie 1., tak?

milciak: Dokładnie

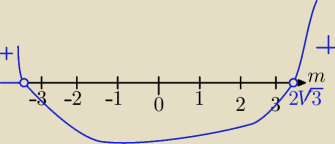
Mila: ad. 23:08 Narysowałam parabolę skerowaną do góry i zaznaczyłam, gdzie wartości dodatnie, popatrz uważnie.

Mila: Dokończ równanie : m⁴+4m³−6m²−32m−16=4m³+6 m² − 32m +12⇔ m⁴−12m²−28=0 Równanie dwukwadratowe: podstawienie: m²=t, t≥0 t²−12t−28=0 dokończ

milciak: Już widzę Δ>0 , czyli wszystkie wartości powyżej osi m.

Mila: Tak.

Martiminiano: Jeśli chodzi o zadanie 1. to zacznę od momentu, o którym piszesz. m²(m−2)−(m−2)>0 Wyłączasz wspólny czynnik, może tak będzie to bardziej widoczne: m²*(m−2)−(m−2)*1>0 (m−2)(m²−1)>0 Drugi nawias rozpisujesz ze wzoru skróconego mnożenia różnica kwadratów: (m−2)(m+1)(m−1)>0 m₁=2 m₂=−1 m₃=1 Nierówność wielomianowa, zaznaczasz pierwiastki, współczynnik przy najwyższej potędze jest dodatni, pierwiastki jednokrotne, więc rysujesz wykres od prawej strony od góry "przebijając" każdy pierwiastek https://matematykaszkolna.pl/strona/145.html Teraz odczytujesz dla jakich wartości parametru jego wykres znajduje się nad osią (bo szukamy dla jakich wartości Δ>0 i nierówność ma dwa pierwiastki) i jest to (−1;1)∪(2;+∞) Teraz przechodzimy do drugiego założenia, a tam jest już wszystko bardzo klarownie wyjaśnione w linku, który wstawiłaś.

milciak: t² − 12t − 28 = 0 Δ= (−12)² − 4 * 1 * (−28)= 144 + 112 = 256 {Δ} = 16 t₁ = − 2 sprzeczność t₂ = 14 m² = 14 m = {14} lub m = − {14}

Martiminiano: Dodam jeszcze tylko, że na końcu biorą część wspólną rozwiązań, bo w tego typu zadaniach szukamy wartości parametrów, dla których spełnione są wszystkie założenia. Tym razem były dwa, a zdarza się więcej i warto o tym pamiętać. Owocnej nauki i dobrej nocy! Powodzenia na sprawdzianie

milciak: Dziękuję bardzo za pomoc! Na pewno się przyda, jak nie na sprawdzian, to na maturę

Mila: m=√14 lub m=−√14 Sprawdzasz czy należą do dziedziny ? √14>√12 i −P{14}<−√12 tak , należą do dziedziny odp. m=√14 lub m=−√14