Zadaniaaa :) Benny: Czyściutko specjalnie dla Mili

Mila: 1) W prostokątnym ΔABC wysokość poprowadzona z wierzchołka kąta prostego podzieliła trójkąt na dwa trójkąty o obwodach 2m i 2n. Oblicz obwód ΔABC.

Mila: 2) Ostrosłup ma w podstawie trójkąt równoboczny o boku 4. Krawędzie boczne mają długości 4, 2, 2√7. Oblicz objętość tego ostrosłupa.

Mila: 3) rozwiąż równanie (x+6+2√x+5)^1₂+(x−2−√x+5)^1₂=4 mają być wszystkie założenia.

Mila: Jaki masz zbiór zadań?

Benny: A no nie mam żadnego

Mila: A podręcznik?

Benny: Znaczy mam podręcznik i zbiór do 3 klasy, ale już dawno przerobiony. Marcin Kurczab, Elżbieta Kurczab, Elżbieta Świda

Mila: To bardzo dobre materiały.

Benny: Zacznijmy od końca. Jaka jest odpowiedz do 3?

Mila: 3) x=4

Benny: To albo odpowiedź jest zła albo źle coś może przepisałaś. Wstaw 4 do równania, nie wychodzi

Mila: Masz rację. Zmieniłam równanie. √x+6+2√x+5+√x−1−√x+5=4 chodziło mi o to abyś zastosował podstawienie √x+5=t Sprawdź w takim razie Twój wynik.

Benny:

	131
mój wynik był		, ale nie wiem czemu jak podstawiam to coś nie idzie
	25

założenia x∊<−1;−5>∪4;+∞ pierwszy czynnik zwija się do wzoru, podstawiam √x+5=t i otrzymuje t+1+√x−1−t=4 3−t=√x−1−t / ()² 9−6t+t²=x−1−t t²−5t−x+10=0 x+5−5√x+5−x+10=0 15=5√x+5 3=√x+5 9=x+5 x=4

Mila: Wynik dobry √(x+6+2√x+5)=√x−1−√x+5 Dlaczego masz w równaniu 2 niewiadome? √x+5=t, t≥0 √(x+5)+1+2√x+5)=√x+5−6−√x+5 Otrzymuję równanie: √t²+2t+1+√t²−t−6=4

Benny: A nie można tak rozwiązywać?

Mila: Jakaś konsekwencja powinna być, podstawienie to podstawienie. Można.

Mila: Dobranoc

Benny: Dobranoc

Mila:

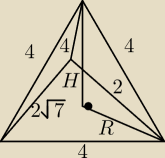
Benny: W książce znalazłem fajne twierdzenia do ostrosłupów, których tam wcześniej nie doczytałem. Jeśli wszystkie krawędzie boczne są równej długości to spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie. Zad 2 Jeśli postawimy ostrosłup na ścianie bocznej 4,2,2√7, to otrzymamy ostrosłup, którego krawędzie boczne są równej długości.

	abc
R=
	4P

P=2√3 z wzoru Herona, (inny sposób?)

	2√21
R=
	3

H²=16−R²

	2√15
H=
	3

	1		2√15
V=		*2√3*
	3		3

	4√5
V=
	3

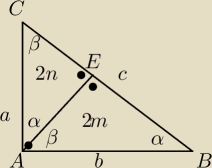
Benny: ΔABE~ΔABC ΔAEC~ABC W−obwód ΔABC

b		2m
	=		/()2
c		W

a		2n
	=		/()2
c		W

a²+b²=c²

b2		4m2
	=
c2		W2

a2		4n2
	=
c2		W2

b²=c²−a²

c2−a2		4m2
	=		| +
c2		W2

a2		4n2
	=
c2		W2

c2−a2+a2		4m2+4n2
	=
c2		W2

	4m2+4n2
1=
	W2

W²=4m²+4n² W=2√m²+n²

Mila: Zadanie2) Właśnie o to michodziło, abyś to zauważył. Wyniki dobre. Pole inaczej można, jeśli boki niewymierne to nie korzystam z wzoru Heron, przewiduję trudności, ale można. 3) Dobrze. Mam trochę mniej obliczeń. W Twoim modyfikuję: (4) i (5) linijkę dodajesz:

b2+a2		4m2+4n2
	=		⇔
c2		L2

	4m2+4n2
1=		⇔
	L2

L=2√m²+n²

Marek: Mila pomożesz ? 287339

Eta: https://matematykaszkolna.pl/forum/249810.html wpis 10 maja 21:18

bezendu: Eta co Ty taka zielona ?

Benny: Tak w ogóle to Wesołych Świąt!

Mila: Wesołych Świąt dla wszystkich

Benny: Jak będziesz miała czas to mogłabyś coś podrzucić?

5-latek: Dajmy dzisiaj spokoj Mili bo pewnie już i tak jest zmeczona . masz tutaj

	x1/2+1		1
Uprosc wyrażenie		:
	x+x1/2+1		x1,5−1

nr2 Rozwiaz układ rownan {lg(x²+y²)−1=lg13 { lg(x+y)−log(x−y)= 3lg2 Nr 3 . Odcinek stycznej zewnętrznej do dwóch okregow o promieniach 5cm i 2 cm jest 1,5 raza weikszy od odcinka stycznej wewnętrznej . wyznacz odleglosc miedzy srodkami tych okregow . nr 4. Podsatwa ostrosłupa prawidłowego jest wielokąt którego suma katow wewnętrznych jest rowna 540 stopni . 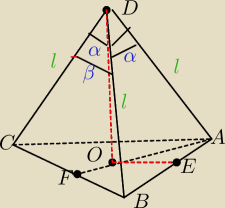Wyznaczyc objetosc tego ostrosłupa jeśli wiadomo ze krawedz boczna jest rowna l i nachylona do płaszczyzny podstawy pod katem α Nr5. Krawedzie boczne ostrosłupa trójkątnego maja jednakowe dlugosci . Z trzech katow płaskich przy weirzcholku ostrosłupa dwa sa rowne α, a trzeci rowny β. Znalezc objetosc ostrosłupa

	3π		π−x
Nr6 . 2[1−sin(		−x)]=√3tg		(Rozwiaz równanie
	2		2

Benny: 1) x−1 2)x,y (9,7)−9,−7)

5-latek: Ale rozwiązanie drugie odrzucamy bo ........

5-latek: Pierwsze oczywiście dobrze jakby ktoś chciał skorzystać to x^1,5−1= (x^1/2)³−1= skorzystać teraz ze wzoru a³−b³

Benny: aj no tak, zapomniałem o dziedzinie

Mila: No i dlaczego tak płaczesz? Albo założenia albo sprawdzasz. log(−9+(−7)) może być?

5-latek: bo ma być x+y>0 i x−y>0 Wesolych Swiat

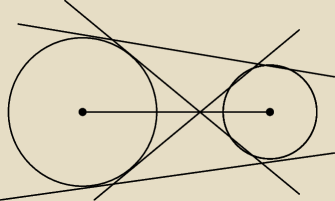
Benny: Może być To zadanko 3 ma mniej więcej wyglądać tak? Bo nie miałem z takim nigdy styczności.

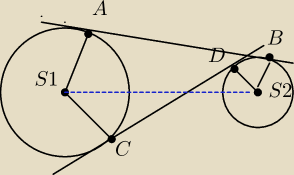
5-latek: Pomysl teraz co dorysować żeby rozwiazac to zadanie

5-latek: W tamtym roku to zadanie dala Eta do rozwiązania dla maturzystów

Benny:

	5
W 4 wyszło mi V=		*sin72o*cos2α*sinα*l3
	2

Benny: zad 6

	π		2π
x=		+2kπ ⋁x=		+2kπ
	3		3

x≠kπ

5-latek: Zadanie nr 4 To nie jest graniastosłup tylko ostrosłup wiec objetosc ostrosłupa V=...

5-latek: Zadanie nr 6

	3π
sin(		−x)=−cosx
	2

	π−x		x
tg(		)= ctg
	2		2

	x		1+cosx
a ctg		=
	2		sinx

Odpowiedzi mama takie

	π
x=π(2k+1) x=πk +(−1)k		k∊C
	3

5-latek:

	1
Vostr=		Pp*H wiec ?
	3

Benny: Tak wiem, zapomniałem dopisać

	5
V=		sin72o*cos2α*sinα*l3
	6

5-latek: Do zadania nr 3 Do rysunku z 22:53 dorysuj prosta rownolegla do AB i przechodzaca przez punkt S₂ Tak samo prosta rownolegla do CD i przechodzaca przez S₂

Mila: No i jak zakończyłeś wszystkie zadania 5− latka, dawać nowe?

Benny: To z tymi okręgami skończyć muszę i w połowie jestem tego 5. "Krawedzie boczne ostrosłupa trójkątnego maja jednakowe dlugosci" mam to traktować tylko jako informację, tak?

5-latek:

5-latek: DO −przechodzi przez srodek okręgu opisanego na trojkacie ABC

	α		β
W tym trojkacie AB=AC=2*lsin		i BC= 2*l *sin
	2		2

Punkt O lezy na prostej prostopadlej EO do boku AB poprwadzonej przez srodek boku AB . Z podobieństwa trojkatow AOE i ABF mamy

AO		AB
	=
0,5AB		AF

	0,5AB2		2*l2sinα/2
AO=		=
	AF		√4*l2*sin2α/2− l2 *sinβ/2

Z trojkata AOD wyznaczymy H

	sin2α−sin2β/2
H= √l2−AO2= l*√
	4sin2α/2−sin2β/2

	1		1		1
Stad mamy V=		*		*BC*AF*H=		*l3*sinβ/2√sin2α−sin2β/2
	3		2		3

5-latek: trochę trudne to było

Benny: Tak, ale zacząłem to właśnie rozwiązywać no ale już to nie ma sensu

5-latek: zadanie nr 3 Bazujemy na rysunku z 22:53 i poscie 05 04 22:06 Prosta rownolegla do AB przetnie promien S₁A w punkcie E Natomiast przez punkt F oznaczmy punkt przecięcia się prostej rownoleglej do CD i przedluzenia promienia S₁ C . Wiec rysuneczek do zadania mamy gotowy . On jest u mnie trochę niedokładny ale TY wiesz jak się wyznacza konstrukcyjnie stycznie do okregow . Teraz W zadaniu mamy dane ze AB=1,5CD jeśli CD=x to S₂F =x a także S₂E = 1,5x Z trojkata S₁E__2 i trojkata S₁FS₂ mam S₁S₂²= S₁E²+(1,5x)² a także S₁S₂²= S₁F²+x² ale S₁E=S₁A_EA= 5−2=3cm S₁F= S₁C+S₂D=5+2=7cm Teraz porównaj te dwa wyrażenia na S₁S₂ i wylicz z tego x Ja tak zrobiłem wtedy to zadanie wyszlo mi 9cm

5-latek: Nie widziałem Twojego wpisu 12:57 i uznałem ze nie dokończysz dlatego napisałem rozwiązania obydwu zadań . No ale może masz inny sposób na rozwiązanie

Benny: Ok Milu, możesz coś wrzucić

Mila: 1) Wyznacz wszystkie wartości parametru k∊R , aby liczba 2 znajdowała sie między miejscami zerowymi funkcji f(x)=x²+4x+k. 2) Jednym z rozwiązan równania : x²−4x+c=0 jest liczba 2+√5. a) Wyznacz wsp. c b) Znajdź drugie rozwiązanie tego równania. ( podaj co najmniej dwa sposoby). 3) Dla jakich wartości parametru m∊R równanie: (m−2)x²+(m−2)x +1=0 ma jedno rozwiązanie?

Benny: Zad 1. Wierzchołek funkcji kwadratowej znajduje się pomiędzy miejscami zerowymi, a>0, więc f(2)<0 z tego wynika, że k<−12 Zad 2. f(2+√5)=0 c=−1 x²−4x−1=0 drugie rozwiązania możemy policzyć z Δ, wzorów viete'a lub jak ja w zeszycie na początku policzyłem jednocześnie c i miejsce zerowe (x−(2+√5))(x−x₂)=x²−x*x₂−x(2+√5) + x₂(2+√5) i tutaj tylko porównałem współczynniki Zad 3. dla m=2 1≠0 więc musi być to równanie kwadratowe, gdzie: m≠2, Δ=0 z Δ otrzymujemy m=2 i m=6, ale m=2 odrzucamy, bo nie należy do dziedziny ostatecznie otrzymujemy jedno rozwiązanie dla m=6

Mila: 4) rozwiąż równanie

	7
√3cosx+sinx=
	4

5) √3cosx+sinx−√2=0

Benny: 5)

	π		√2
sin(		+x)=
	3		2

	π		5π
x=−		+2kπ ∨ x=		+2kπ
	12		12

	π		7
zad 4 robiłem tak samo, ale otrzymuję sin(		+x)=		i tego nie wiem jak ruszyć,
	3		8

spróbuje innym sposobem

Mila: W czwartym oblicz przybliżoną wartość.

Benny:

	7		π
sinα=		to jest jakieś 61o więc
	8		3

	π
x=2kπ ∨ x=		+2kπ
	3

Mila: 6) Dane są dwa zbiory: A={1,2,3,...,62} i B={1,2,3,...,124}. Losowo wybieramy zbiór a z niego losujęmy liczbę n. Oblicz prawdopodobieństwo, że liczba n²+1 będzie podzielna przez 10.

Mila:

	π		π
4) x≈61o−		+2kπ lub x≈π−61o−		+2kπ
	3		3

Przybliżona wartość liczysz, gdy masz w poleceniu. Zapomniałam dodać.

Benny: Ok, ale to moje jest dobrze czy nie? Bo tak zapisałaś, że nie wiem o co chodzi

Mila:

	π		7		π
sin(x+		)=		więc obliczyłam x, gdy Ty odczytałeś wartość dla α=x+		)
	3		8		3

PR: Jeśli mogę. Milu jak zrobić to prawdopodobieństwo? Nie mam pojęcia jak to ugryźć

Benny: Ok Zad 6 jeśli n²+1 ma się dzielić przez 10, to n² musi mieć cyfrę jedności 9 no i tutaj zobaczyłem, że liczba z cyfrą jedności 3 lub 7 podniesiona do kwadratu ma cyfrę jedności 9 więc w zbiorze A jest takich liczb 11 a w B 24, więc:

	1		11		1		24		23
P(A)=		*		+		*		=
	2		62		2		124		124

Mila: Kwadrat wylosowanej liczby musi miec cyfrę jedności 9. Ze zbioru A będą to liczby: 3,13,23,33,43,53,7,17,27,37,47,57 − 12 liczb W zbiorze B jest 25 takich liczb: 3,13,23,33,43,53,63,73,83,93,103,113,123,7,17,27,37,47,57 ,67,77,87,97,107,117 − 25 liczb

	1		12		1		25
P(A)=		*		+		*
	2		62		2		124

Benny: Aj miałem tak napisane w zeszycie, że dwie liczby wziąłem jako 1 i policzyłem jeszcze raz i wyszło dobrze

PR: Dziękuję Wszystko idzie ładnie tylko to prawdopodobieństwo....

PR:

	1
Tam jest		bo są 2 zbiory czy dlaczego?
	2

Benny: tak, możesz sobie to zapisać tak |Ω|=2

	1
więc na wylosowanie jednego zbioru masz
	|Ω|

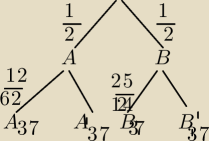Mila: PR w zadaniu podane, że najpierw wybierasz losowo zbiór, dlatego jest pomnożone przez

	1
		.
	2

A_(3,7)={3,13,23,33,43,53,7,17,27,37,47,57 } liczba z cyfrą jedności 3 lub 7 B_(3,7)= {3,13,23,33,43,53,63,73,83,93,103,113,123,7,17,27,37,47,57 ,67,77,87,97,107,117} − liczba z cyfrą jedności 3 lub 7

PR: Dziękuję Pani Milu

Benny: Dziękuje za dzisiejsze zadanka. Dobranoc

Mila: Dobranoc.

Benny: Milu, jak udowadniać nierówności za pomocą pochodnej? mam np. takie równanie: dla x>0

	16
x2+		≥12
	x

	16
robię taką funkcje f(x)=x2+		−12
	x

	16
f'(x)=2x−
	x2

no i tu próbuje wykazać, że jest zawsze dodatnia, ale coś nie pyka

Eta: Z nierówności między średnimi am −gm x>0

8   8   x2+ +   x   x		8		8
	≥3√x2*		*		= 4
3		x		x

	16
to x2+		≥12
	x

c.n.u

Eta: Przepraszam ,że się wcięłam ( bo to był post skierowany do Mili

Braun: Wybaczam !

Eta:

Benny: Dziękuje Eta Wiem jak rozwiązać taką nierówność chociażby jako zwykłą nierówność wielomianową, ale specjalnie zaznaczyłem "za pomocą pochodnej"

Benny: To co z tą pochodną?

Mila: To nie tylko pochodna, ale ekstrema, czasem granice, zbiór wartości. Ten przykład to sposobem Ety albo innym, możesz pomnożyć przez mianownik. W książce masz takie polecenie do tej nierówności?

	2x3−16
f'(x)=		, x>0
	x2

f'(x)>0⇔2x³−16>0⇔ x³−8>0⇔x>2⇔f(x) rosnąca dla x>2 f(x) malejąca dla x∊(0,2) f'(x)=0⇔x=2 dla x=2 funkcja f(x) ma minimum f(2)=0

	16
Zatem f(x)=x2+		−12≥0 dla x∊(0,∞)
	x

Benny: Nie wiem jakie było polecenie, bo zauważyłem jak na tablicy było to robione i pomyślałem o pochodnej Ogólnie to jak zabierać się za takie nierówności za pomocą pochodnej?

Mila: No przecież pokazałam.

Benny: No tak, wiem Więc przy każdym takim przykładzie najlepiej liczyć granicę, ekstrema i zbiór wartości?

Mila: Wszystko zależy jaka to nierówność. Pochodna to nie jest lekarstwo na wszystko. Odpuść to sobie. Rozwiązuj zadania typowo maturalne.

Benny: No, ale jak patrzyłem na zadania.info to trafiło się takie zadanko, więc wole się upewnić

Benny: a masz coś może ciekawego do zaoferowania?

Mila:

	x2−4
1) Wyznacz równanie stycznej do wykresu funkcji f(x)=
	x2+x+1

	5
w punkcie P (x0,		).
	4

Ile punktów wspólnych z wykresem funkcji ma ta styczna?

	x2
2) Wyznacz równanie stycznej do wykresu funkcji f(x)=		w punkcie P(x0),−9).
	x+2

Ile punktów wspólnych z wykresem funkcji ma ta styczna?

Benny: pierwsze coś nie pyka zad 2

	x2
−9=
	x+2

x=−6 lub x=−3 więc są dwa punkty(dwie styczne) P₁(−3;−9), P₂(−6;−9)

	x(x+4)
f'(x)=
	x+2

f'(−3)=3=f'(−6) y+9=3(x+3) lub y+9=3(x+6) y=3x lub y=3x+9 dla pierwszej są dwa punkty wspólne, P₁(−3;−9) P₂(0;0)

	3		9
dla drugiej P1(−6;−9), P2(−		;		)
	2		2

Mila: Ach to kopiowanie! Przepraszam. W pierwszym

	x2−4
f(x)=
	x2+2x+1

W drugim masz źle obliczoną pochodną.

Benny: aj no tak kwadrat w mianowniku

Benny: Poprawka:

	x(x+4)
f'(x)=
	(x+2)2

y₁=−3x−18

	3		9
y2=		x−
	4		2

mają po jednym punkcie styczności y₁ ma w P(−3;−9) y₂ w P(−6;−9) chyba teraz dobrze

Benny: W tym pierwszym takie duże ułamki wychodzą?

Mila: (2) dobrze.

	1		13
(1) y=		x+
	36		9

	1		1
y=−		x+
	4		2

Mila: Jutro nowy wątek. Dobranoc

Benny: Coś musiałem źle dodać, zmęczenie wygrało. Dobranoc

Benny: Jak coś to nowy wątek https://matematykaszkolna.pl/forum/288381.html

Eta: 100 moja

Mila: Jubileusz. A ja już zasypiam, witam i żegnam. Dobranoc Jutro sprawdzę.

Benny: Dobranoc