Nowe, puste miejsce Benny:

	x2−4		5
Wyznacz równanie stycznej do wykresu funkcji f(x)=		w punkcie P (x0;		)
	x2+2x+1		4

Ile punktów wspólnych z wykresem funkcji ma ta styczna?

5		x2−4
	=
4		x2+2x+1

5x²+10x+5=4x²−16 x²+10x+21=0 x₁=−7, x₂=−3

	5		5
P2(−7;		), P1(−3;		)
	4		4

	2x+8
f'(x)=
	(x+1)3

	1
f'(−3)=−
	4

	1
f'(−7)=
	36

	1		5
y1=−		*(x+3)+
	4		4

	1		1
y1=−		x+
	4		2

	1		5
y2=		*(x+7)+
	36		4

	1		13
y2=		x+
	36		9

Punkty wspólne: y₁=f(x)

	1		1		x2−4
−		x+		=
	4		2		x2+2x+1

2−x		x2−4
	=
4		x2+2x+1

4x²−16=−x³+3x+2 x³+4x²−3x−18=0 (x−2)(x+3)²=0

	5
punkty wspólne P1(−3;		), Q1(2;0)
	4

y₂=f(x)

x+52		x2−4
	=
36		x2+2x+1

36x²−144=x³+54x²+105x+52 (x+4)(x+7)²=0 Punkty wspólne

	5		4
P2(−7;		), Q2(−4;		)
	4		3

Mila:

Benny: Milu spojrzysz? https://matematykaszkolna.pl/forum/288425.html Liczę i coś mi nie wychodzi. Może sposób zły? Robiłem to tak:

⎧	y=ax+b
⎩	y=x2

⋀

⎧	y=ax+b
⎩	x2+(y+2)2=4

Myślałem też aby zapisać styczną do paraboli przez pochodną. Co myślisz?

Mila: Zadanie jest z płatnego forum, to raz, dwa nie mam na razie dobrego pomysłu. (chyba?)

Mila: Rozwiązuj coś innego.

Radek: Pani Milu pomoże Pani z układem równań ?

Mila: Gdzie jesteś Radku?

Benny: Wiem, że jest z płatnego forum. Nie liczyłem na rozwiązanie zadania, lecz na jakąś wskazówkę

Benny: Przypomniało mi się zadanko. Jak byś je rozwiązała? Wartość funkcji g w punkcie m jest równa sumie pierwiastków równania |mx²−2x|=m, przy czym każdy pierwiastek jest w tej sumie uwzględniany tylko raz niezależnie od jego krotności. Znajdź funkcję g : m→g(m) i naszkicuj jej wykres.

Qulka: podstawić y=ax+b do kółka i do paraboli i delta równa zero dla obu wynik to y=±2√6−6

Qulka: oprócz tego y=0

Qulka: zjadłam x miało być y=±2√6x−6

Mila: Liczyłaś ? , bo ja mam dziś niechęć do dużych rachunków. Radkowi rozwiązałam równanie.

Qulka: liczyłam i nawet szybko się liczy

Qulka: ja miałam łatwiej, bo to nie ja musiałam pisać tylko mówiłam co liczyć

Mila: Ja też zjadłam x.

Blue: To zadanie nie jest wcale takie trudne, mogę Wam wstawić rozwiązanie swoje

Mila: Oj, nie wstawiaj. Mówisz o stycznych, czy tym drugim. Mnie się nie chciało dzisiaj liczyc.

Blue: Mówię o stycznych

Blue: http://i60.tinypic.com/2lvlfzc.jpg − Proszę, skoro już się przekopałam przez tę stertę arkuszy

Qulka: faktycznie √5 jakoś mi się kojarzy

Mila: Jutro policzę dwoma sposobami. Dziękuję . Dobranoc

Qulka: https://matematykaszkolna.pl/forum/288425.html

Qulka: rozpisałam

Benny: Ok, dzięki. Robiłem dobrze, bo widzę po rachunkach Qulki. Miałem jakiś błąd rachunkowy w Δ. Drugi sposób o którym myślałem, ze styczną z pochodną też widzę by się sprawdził

Benny: Hej Milu Miałabyś może jakieś zadanka z dowodami geometrycznymi? Coś czuję, że ich nie ogarniam.

Mila: Znajdzie się. Z pochodną, chyba mniej żmudne obliczenia.

Mila: 1) Wykazać, że w trójkącie prostokątnym kwadrat długości przyprostokątnej jest równy iloczynowi długości przeciwprostokątnej przez długość rzutu prostokątnego tej przyprostokątnej na przeciwprostokątną. 2) Wykazać, że w trójkącie prostokątnym suma odwrotności kwadratów długości przyprostokątnych jest równa odwrotności kwadratu długości wysokości poprowadzonej do przeciwprostokątnej. 3) Na przeciwprostokątnej AB trójkąta prostokątnego ABC wybrano punkty D i E w taki sposób, by AC = AE oraz BC = BD. Udowodnij, że ∡DCE = 45^o. 4) W równoległoboku ABCD, w którym bok AB jest dwa razy dłuższy od boku BC, połączono środek M boku AB z wierzchołkami C i D. Udowodnij, że kąt CMD jest prosty. 5) Wykaż, że jeżeli α≤β≤γ są kątami wewnętrznymi trójkąta rozwartokątnego, to: sin²α<sin²γ−sin²β

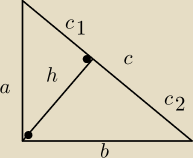
Benny: 1) Muszę się przyznać, nie wiedziałem, który odcinek będzie rzutem. c₁+c₂=c a²=h²+c₁² h=√c₁*c₂ a²=c₁*c₂+c₁² a²=c₁(c₂+c₁) a²=c₁*c

Benny:

	a*b		h*c
P=		=
	2		2

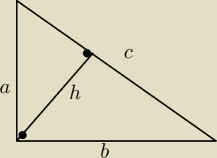
a*b=h*c a²+b²=c²

1		1		a2+b2		c		c		1
	+		=		=(		)2=(		)2=
a2		b2		a2*b2		a*b		h*c		h2

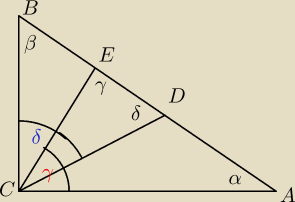
Benny: 3) α+β=90^o 90^o+2γ+2δ=360 γ+δ=135^o γ+δ+∡DCE=180^o ∡DCE=180^o−135^o ∡DCE=45^o

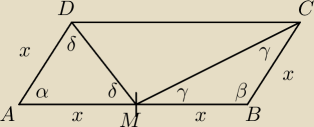
Benny: 4) Analogicznie jak 3? α+β=180^o a+β+2γ+2δ=360^o γ+δ=90^o γ+δ+∡DMC=180^o ∡DMC=90^o

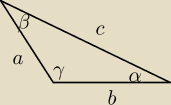
Benny: W trójkącie rozwartokątnym mamy zależność: a²+b²<c² z tw. sinusów

a		b		c
	=		=		=2R /()2
sinα		sinβ		sinγ

a²=4R²*sin²α b²=4R²*sin²β c²=4R²*sin²γ 4R²*sin²α+4*R²*sin²β<4R²*sin²γ /:(4R²) sin²α+sin²β<sin²γ sin²α<sin²γ−sin²β

Mila: Optymalizacja.?

Benny: W sensie czy robimy?

Mila: 6) Przekątna prostopadłościanu tworzy ze ścianami majacymi wspólny wierzchołek kąty: α,β,γ. Uzasadnij, że: sin²α+sin²β+sin²γ=1

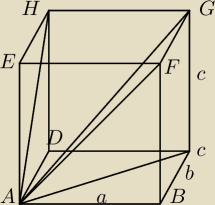
Benny: kątów nie oznaczę, bo wąskie linie Kurcze nie umiem takiego dokładnego rysunku tu zrobić, żeby to ładnie pokazać. α−∡HAG β−∡FAG γ−∡GAC

	a
sinα=
	√a2+b2+c2

	b
sinβ=
	√a2+b2+c2

	c
sinγ=
	√a2+b2+c2

	a2		b2		c2
sin2α+sin2β+sin2γ=		+		+		=
	a2+b2+c2		a2+b2+c2		a2+b2+c2

	a2+b2+c2
=		=1
	a2+b2+c2

Maksym: 1) Przedstaw liczbę 12 w postaci iloczynu takich dwóch liczb rzeczywistych dodatnich, aby suma czynników tego iloczynu. 2) Na paraboli o równaniu y=x² znajdź punkt P leżący najbliżej punktu B=(3,0)

Mila : Całkiem ładnie opisałeś ten prostopadłościan.

Mila:

Mila: 7) Rozpatrujemy wszystkie graniastosłupy prawidłowe czworokątne o polu powierzchni całkowitej równym P. Wskaż wśród nich graniastosłup o największej objętości.

Benny: 7) P=2a²+4ab P−2a²=4ab

	P−2a2
b=
	4a

V=a²*b

	P*a−2a3
V(a)=
	4

	P−6a2
V'(a)=
	4

P−6a²=0

	−√P		√P
a=		∨ a=
	√6		√6

	√P
V max dla a=
	√6

	P   P−   3
b=
	4a

	2P
4ab=
	3

P=6ab 6ab=2a²+4ab 2ab=2a² a=b Największą objętość będzie miał sześcian

Mila: Zgadza się.

Mila: 8) Rozpatrujemy wszystkie trapezy równoramienne o obwodzie równym 4p i kącie ostrym 60^o. Wyznacz wymiary takiego trapezu, który ma największe pole.. Oblicz to pole.

Mila: 9) Rozpatrujemy wszystkie walce o polu powierzchni całkowitej równym P. Wskaż wśród nich walec o największej objętości.

Benny: Dziękuje, te dwa dokończę jutro. Dobranoc

Mila: Dobranoc

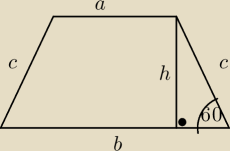
Benny: 8) 4p=a+b+2c

a+b
	=2p−c
2

h		√3
	=
c		2

	√3c
h=
	2

	√3c
P=(2p−c)(		)
	2

	√3c2
P(c)=√3pc−
	2

	b
−		=p
	2a

c=p

	p2√3
P=
	2

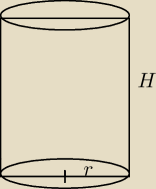
Benny: 9) P=2πr²+2πrH 2πrH=P−2πr²

	P−2πr2
H=
	2πr

	P−2πr2
V=πr2*
	2πr

	P*r−2πr3
V=
	2

	P−6πr2
V'(r)=
	2

	P
6π(		−r2)=0
	6π

	√P
V max dla r=
	√6π

	P
P=		+2πrH
	3

P=3πrH 3πrH+2πrH+2πr² πrH=2πr² H=2r V=2πr³

Mila: Zgadza sie z moimi rachunkami. Nie mam odpowiedzi do zadania.

	P*√6πP
V=
	18π

Może ktoś ma ksążkę z tymi zadaniami to pewnie kiedys tu spojrzy.

Mila: W trapezie nie podałeś wymiarów, z wyjątkiem c.

Mila: Tu masz ciekawe zadanie. https://matematykaszkolna.pl/forum/289189.html

Benny: Nie wiedziałem, że wszystkie odcinki trzeba podać. Tak więc:

	3
a=		p
	2

	1
b=		p
	2

Mila: Było polecenie: wyznacz....

Benny: Korzystając z Twojego rysunku, jeśli jako "b" oznaczymy krawędź przekroju to:

a2
	=1−cosβ, przyda się to w ogóle, bo nie wiem czy wyznaczać to "b"?
b2

Mila: Odcinek b oblicz z Δ w którym dany jest kąt α, tam jest Δprostokatny . Tu wrzucę zadanka.

Benny: Coś nie za bardzo mi się ten kąt prosty widzi.

Mila: 2) Wyznacz iloraz różnicowy funkcji f(x) w punkcie x₀. Obliczenia wykonaj dla przyrostu Δx=0,01 a) f(x)=−3x+2 , x₀=3

	1
b) f(x)=		, x0=0
	2x+1

3) Napisz równanie stycznej ( w postaci ogólnej) do wykresu funkcji f(x), wiedząc, że ta styczna jest równoległa do prostej k. f(x)=x²+2x−3 , k: 4x−y−1=0 4) Napisz równanie stycznej ( w postaci ogólnej) do wykresu funkcji f(x), wiedząc, że ta styczna jest prostopadła do prostej k. f(x)=3x²−x+2 , k:x+5y−15=0

Mila: Do jutra. Dobranoc

Benny: 2)

	f(x0−Δx)−f(x0)
a)		=3
	Δx

	48
b)−98
	49

Dobranoc

Benny: 3) k: y=4x−1 więc równoległa będzie: y=4x+b f'(x)=4 f'(x)=2x+2 2x+2=4 ⇒ x=1 f(1)=0 P(1;0) y=4x+b, 0=4+b ⇒b=−4 prosta ma równanie: −4x+y+4=0 4)

	x
k: y=3−
	5

więc prostopadła będzie y=5x+b f'(x)=5 f'(x)=6x−1 6x−1=5 ⇒ x=1 f(1)=4 P(1;4) 4=5+b ⇒ b=−1 prosta ma równanie: −5x+y+1=0

Mila: Tak

Benny: Jeszcze coś tam masz?

Benny: No i z tym ostrosłupem to nadal nie widzę trójkąta prostokątnego z kątem α

Mila: Jeżeli prosta przebija płaszczyznę i jest do niej prostopadła , to jest prostopadła do każdej prostej leżącej w płaszczyźnie i przechodzącej przez punkt przebicia. Uff!

Mila: Mam zadanka, ale za chwilę będę zajęta. 1) Rozwiąż równanie : a²*(x−1)+a*(2x−1)=3x−2 z niewiadmą x i parametrem a∊R. 2) Dla jakich wartości parametru p pierwiastki x₁,x₂ równania : x²−px+4=0 należą do zbioru R₊ i takich , że ||x|−2|<2.

Benny: ∡BEC jest prosty? Jeśli tak to chyba błąd był w złym określaniu kąta prostego zaznaczonego na rysunku.

Benny: Z tego pierwszego wyznaczyłem x i otrzymałem:

	a2+a−2
x=
	a2+2a−3

mianownik zeruje się dla a=−3 i a=1 dla a=1 jest tożsamość, a dla a=−3 sprzeczność więc dla a∊R/{−3;1} jest jedno rozwiązanie

Benny: 2) dałem warunki: x₁*x₂>0 x₁+x₂>0 Δ≥0 wyszło p∊(−∞;−4>∪<4;+∞) rozwiązałem wartość bezwzględną i dostałem x∊<−4;4>, ale x∊R₊ to x∊<0;4> Nie jestem do tego zadanka przekonany.

Benny:

Mila: 1) a≠−3 i a≠1 istnieje dokładnie jedno rozwiązanie

	(a+2)*(a−1)
x=		⇔
	(a+3)*(a−1)

	a+2
x=
	a+3

2) dla a=−3 brak rozwiązań 3) dla a=1 każda liczba x∊R spełnia równanie: mamy taką sytuację: (1+3)*(1−1)*x=(1+2)*(1−1)⇔ 4*0*x=3*0

Mila: 2) Mam p∊(4,5) Rozwiąż warunek, że x₁,x₂∊(0,4) ,

Benny: Tam u mnie źle rozpisana wartość bezwzględna powinny być otwarte przedziały. x∊(0;4) Coś nadal mi nie pasuje z Twoim rozwiązaniem. Po otrzymaniu dziedziny x∊(0;4), nie rozważam już iloczynu oraz sumy dodatniej tylko: Δ≥0 0<x_w<4 f(0)>0 f(4)>0 z Δ mam p∊(−∞;−4>∪<4;+∞) z wierzchołka p∊(0;8) z miejsc zerowych p∊(−∞;5) Z wszystkich warunków dostaje: p∊<4;5) Z Twojej odpowiedzi wynika, że warunek z Δ mam zły, ale nie wiem dlaczego, nie ma żadnej informacji o różnych miejscach zerowych.

Benny: Milu, przeanalizujesz? Nie widzę błędu

Mila: Z wartości bezwzględnej masz x∊(−4,4)

Benny: No tak, ale jaki to ma związek z p?

Mila: Wyrzuciłam wczoraj kartkę, już liczę.

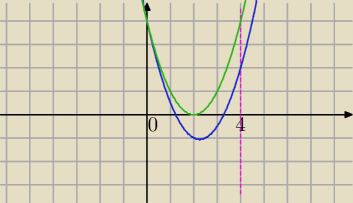
Mila: 2) x²−px+4=0 (1)Δ≥0⇔p≤−4 lub p≥4 (2) x₁+x₂>0⇔p>0 x₁*x₂=4>0 dla każdego p∊D 3) ||x|−2|<2 i x>0⇔x∊(−4,4) 4) x₁,x₂ dodatnie i x₁,x₂∊(−4,4) ⇔x₁,x₂∊(0,4) Rysuję sytuację : f(0)>0 i f(4)>0 f(0)=4dla p∊R i f(4)=−4p+20>0 ⇔p<5 p∊<4,5) dla p=4 zielony wykres. p=4.5 niebieski Nie wiem dlaczego tak wczoraj napisałam, mam w zeszycie przedział <4,5). Coś jeszcze się nie zgadza?

Mila: Rozwiązujesz testy?

Benny: Teraz już się zgadza. Poprawiłem w końcu polski, więc jutro zabieram się za zadania.info, ale chętnie rozwiąże jak coś masz

Mila: Co to znaczy poprawiłeś, coś Ci groziło?

Benny: Tak, wymagająca nauczycielka, pół klasy miało zagrożenie, ale przynajmniej sobie powtórzyłem dodatkowo pare lektur

bezendu: Mila a czemu poprawiał, jasna rzecz brak dopuszczenia do matury..

Mila: To były strachy na Lachy. Benny Ty wrzucaj zadania z problemami.

Benny: Jasne, ale to już nie dziś.

Benny: Dobranoc

Mila: 1) Dla jakiej wartości parametru p równanie f(x)=1 ma dokładnie 3 rozwiązania, gdzie f(x)=x²−4|x−1|−p

Benny: Zrobiłem to tak:

	⎧	x2−4x+4, dla x≥1
f(x)=	⎩	x2+4x−4, dla x<1

Narysowałem ten wykres i prostą y=1 i o dziwo od razu się przecięły w trzech miejscach. Wynika z tego, że dla p=0 równanie ma 3 rozwiązania. Oczywiście, jeśli by się nie przecięły dobierałbym takie p, żeby prosta y=1 przecinała w trzech miejscach wykres

PR: A mi wyszło p=−1 lub p=0

Benny: Rzeczywiście dla p=−1 też wyjdzie

Benny: Nie popatrzyłem dobrze na wykres, ale rozwiązanie graficzne jest dobre?

PR: Tak, tylko nie zapomnij o przyrównaniu f(x)=p

Benny: Rozwiąż równanie: 2sinx+tgx=0 cosx≠0

2sinx*cosx		sinx
	+		=0
cosx		cosx

sin2x+sinx
	=0
cosx

sin2x+sinx=0

	3x		x
2sin		*cos		=0
	2		2

3x		x		π
	=kπ ⋁		=		+kπ
2		2		2

	2kπ
x=		⋁ x=π+2kπ
	3

	π
x≠		+kπ
	2

Czy może jakoś inaczej to zrobić?

Benny:

	2		7
Wyznacz liczbę a>1, która spełnia równanie 2a2+		=7a+
	a2		a

Nie mogę tego rozłożyć. W wolframie wychodzi a₁=2−√3 a₂=2+√3. Jest na to inny sposób?