:) :): Ostrosłup prawidłowy czworokątny przecięto płaszczyzną zawierającą przekątna podstawy i prostopadłą do jednej z krawędzi bocznych. Wiadomo, że kąt między krawędzią boczna ostrosłupa a krawędzią podstawy jest równy α, gdzie α∊(45^o,90⁰). wykaż że cosinus największego kąta otrzymanego przekroju jest równy U{−1}{tg²α). Może ktoś to narysować?

===:

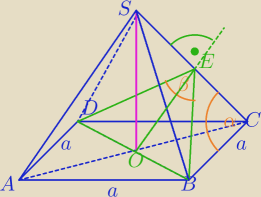
Mila: OE⊥CS

:): dziękuje