Witam
Marek: Hej. Jak rozróżnić. Wariację z powtórzeniami i bez, permutację, kombinację?
2 kwi 21:29
5-latek: Czesc
jak się ożenisz to zrozumiesz co to sa np. wariacje z powtórzeniami lub bez

2 kwi 21:46
Mila:

2 kwi 21:48
Marek: Hahaha

2 kwi 21:49
Mila:
Szukam Linka z teorią dobrze wytłumaczoną przez Gustlika.
Czekaj.
2 kwi 21:50
5-latek: Dobry wieczor
Milu 
Pozdrawiam

jak daleko przygotowania do Swiat?
2 kwi 21:51
Qulka:
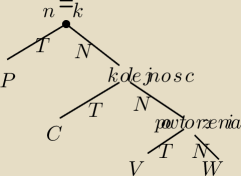
2 kwi 21:52
Qulka: pomyliłam wariacje powinno być W pod Tak i V pod nie
2 kwi 21:52
2 kwi 21:56
bezendu:
Mi też się to przyda !
2 kwi 21:58
Mila:
Witaj kolego 5− latku, wszystkie produkty kupione, zorganizowane, przygotowania w toku,
dzisiaj płakałam nad chrzanem ( mocno wyciskał łzy).
A u Ciebie?
2 kwi 21:58
Marek: Dziękuję!
Liczę bardziej na wskazówki niż rozwiązania gotowe. Dla Was to mnie pracy a ja więcej będę
czerpał

Oblicz prawdopodobieństwo tego, że w 4 osobowej rodzinie co najmniej 2 osoby urodziły się w tym
samym miesiącu ?
2 kwi 21:59
5-latek: Milu 
Porzadki już porobione . Najwazniejszse sledzie zrobione ,biala kielbasa i jajka kupione
dzisiaj w nocy wraca corka z Niemiec to napieka z zona ciasta bo obie kucharki
2 kwi 22:06
Mila:
Tylko czekamy na pogodę.

2 kwi 22:13
Mila:
Marku , skorzystaj ze zdarzenia przeciwnego − każda z 4 osób urodziła się w innym
miesiącu.
2 kwi 22:15
5-latek: Tak
Milu czekamy na pogode
Bo żeby nie było tak ze będziemy jajka na choince wieszać

2 kwi 22:15
Metis: U mnie
śniegowo 
2 kwi 22:15
Marek: Dziękuję! Wyszło

2 kwi 22:23
2 kwi 22:27
Marek: Oblicz prawdopodobieństwo tego, że w 4 osobowej rodzinie dokładnie 2 osoby urodziły się w tym
samym miesiącu.
Próbuje ale niestety coś robię źle.
2 kwi 22:33
Marek: Dziękuję

2 kwi 22:34
Mila:
1) wybieramy 2 osoby które urodziły się w tym samym miesiącu − kombinacje
2) wybieramy miesiąc w którym para ta urodziła się − kombinacja
3) pozostałe 2 osoby urodziły się w różnych miesiącach i innych niż ta poprzednia dwójka .
2 kwi 22:40
Marek: Zapomniałem o kombinacji nr 1

Dziękuję
2 kwi 22:42
Mila:

2 kwi 23:03
Marek: Nauczycielka wspominała nam też o "drzewkach" do czego służą?
2 kwi 23:11
Mila:
Do ilustracji przebiegu doświadczenia losowego i do obliczania prawdopodobieństwa.
2 kwi 23:14
Marek: W urnie jest 6 kul białych i k razy więcej kul czarnych. Oblicz k jesli przy jednoczesnym
losowaniu dwóch kul prawdopodobieństwo otrzymania kul o roznych kolorach jest równe
3 kwi 13:38
3 kwi 13:43
Marek: Dzięki

3 kwi 13:48
Marek: Grupę 12 uczniów, wśród których jest 6 dziewczynek i 6 chłopców podzielono na 3 równoliczne
grupy. Oblicz prawdopodobieństwo tego, że w każdej z utworzonych grup będzie tyle samo
dziewcząt.
3 kwi 20:04
3 kwi 21:15
Marek: Spośród liczb 1,2,3,...n (n≥3) losujemy kolejno bez zwracania 2 liczby.
Oblicz prawdopodobieństwo tego że pierwsza z wylosowanych liczb jest większa od 2.
Omega mi wyszła n(n−1)
Tylko nie wiem co dalej. Próbowałem coś z (n−1) na pierwszym miejscu.
3 kwi 21:49
Mila:
(a,b) , a>b ⇔ciąg dwuwyrazowy malejący
| |
−na tyle sposobów możesz wylosować dwuwyrazowe ciągi malejące ze zbioru n− elementów. |
| |
3 kwi 21:56
3 kwi 21:59
Mila:
W której jesteś klasie, bo nie wiem jak Ci mam tłumaczyć.
3 kwi 22:10
Marek: 4 technikum.
| | | |
Według mnie to | losujemy wszystkie dwuwyrazowe a nie tylko malejące..proszę o |
| | |
wytłumaczenie.
3 kwi 22:29
Mila:
Wszystkie dwuwyrazowe to juz napisałeś:
n*(n−1) i połowa z nich to ciągi rosnące a połowa to ciągi malejące.
Z= {1,2,3,4}
{1,2},{2,1}
{1,3},{3,1}
{1,4},{4,1}
{2,3},{3,2}
{2,4},{4,2}
{3,4},{4,3}
Znajdę materiały to Ci napiszę więcej teorii, gdzieś mam to zapisane.
3 kwi 22:51
Marek: Dziękuję

Oczywiście czekam na materiały

3 kwi 23:01
Jacek: To jest pytanie czy pierwsza wylosowana jest większa od drugiej czy od liczby=2?
4 kwi 00:19
Marek: 4) W urnie znajduję się n (n>0) kul białych oraz kn kul czarnych, gdzie k jest liczbą naturalną
dodatnią. Z urny losujemy 2 kule bez zwracania.
a) wykaż, że prawdopodobieństwo wylosowania 2 kul o różnych kolorach jest równe
prawdpodobieiństwu wylosowania 2 kul o takim samym kolorze wtedy i tylko wtedy, gdy n=
I dlaczego to k>1?
4 kwi 13:40
Marek: ?
4 kwi 18:00
Qulka: żebyś nie miał ujemnej w nawiasie
4 kwi 18:02
Qulka: poza tym żeby mówić o wylosowaniu różnokolorowych trzeba mieć przynajmniej jedną czarną
4 kwi 18:03
Marek: Jest tak ponieważ liczba kul musi być dodatnia?
Dziękuję

4 kwi 18:28



 Pozdrawiam
Pozdrawiam  jak daleko przygotowania do Swiat?
jak daleko przygotowania do Swiat?
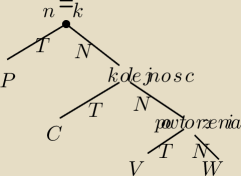
 Oblicz prawdopodobieństwo tego, że w 4 osobowej rodzinie co najmniej 2 osoby urodziły się w tym
samym miesiącu ?
Oblicz prawdopodobieństwo tego, że w 4 osobowej rodzinie co najmniej 2 osoby urodziły się w tym
samym miesiącu ?
 Porzadki już porobione . Najwazniejszse sledzie zrobione ,biala kielbasa i jajka kupione
dzisiaj w nocy wraca corka z Niemiec to napieka z zona ciasta bo obie kucharki
Porzadki już porobione . Najwazniejszse sledzie zrobione ,biala kielbasa i jajka kupione
dzisiaj w nocy wraca corka z Niemiec to napieka z zona ciasta bo obie kucharki





 Dziękuję
Dziękuję


 Oczywiście czekam na materiały
Oczywiście czekam na materiały 
