rownania z wartoscia bezwzgledna
Rose: Pomocy



jak rozwiazac:
|x
2−4|+|x
2−1|=4x+1



9 lut 20:27
Patryk: |x−2|*|x+2|+|x−1|*|x+1|=4x+1
9 lut 20:29
Rose: i co dalej?
bo nadal nie wiem jak to zrobic
9 lut 20:30
Rose: blagam pomozcie
9 lut 20:33
Patryk: Nie wiem czy jest prostszy sposób, ale tak jak ja napisałem, też można zrobić.
musisz wyznaczyć przedziały i obliczać dla każdego przedziału wartości.
9 lut 20:36
Rose: moglbys zaczac bo ja nadal nie kumam do konca
9 lut 20:36
Patryk: Tak jak tutaj
1796, tylko że u Ciebie będzie 5 przedziałów, a nie 3.
9 lut 20:37
Patryk: Chwila, rozpiszę to
9 lut 20:37
Rose: o to moze napisz same przedzialy czy cos
bo takie 1796 umiem robic ale tu jakos nie za bardzo mi idzie
9 lut 20:38
Rose: ok
9 lut 20:38
Abey: Autorowi raczej nie chodzi o rozwiązywanie w przedziałach...
Trzeba pewnie wpaść na jakiś pomysł.
9 lut 20:40
Rose: byc moze
ale trzeba wiedziec na jaki
9 lut 20:40
Rose: to znaczy u mnie to jest dzial funkcja kwadratowa moze to komus cos pomoze...
9 lut 20:41
Rose: wg mnie lepiej miec za pomoca samych przedzialow niz w ogole tego nie miec
9 lut 20:42
Rose: a tak poza tym jak zachowuja sie iksy w tych przedzialach?
9 lut 20:44
Abey: Zauważ że |x
2−4|+|x
2−1| ≥ 0 dla dowolnego x∊R.
Zatem szukamy rozwiązań tylko na dodatniej osi iksów. Będzie troche mniej przedziałów

9 lut 20:44
Patryk:
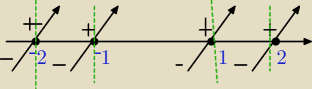
x−2≥0 ⇒ x≥2
x+2≥0 ⇒ x≥−2
x−1≥0 ⇒ x≥1
x+1≥0 ⇒ x≥−1
Czyli przedziały:
1. (−
∞,−2)
2. <−2,−1)
3. <−1,1)
4. <1,2)
5. <2,+
∞)
9 lut 20:44
9 lut 20:45
Rose: dzieki
 Patryk
Patryk
9 lut 20:47
Abey: Troche zle powiedzialem. Skoro lewa strona jest nieujemna, to prawa też, więc
9 lut 20:47
Patryk: bardziej na tym się wzoruj, bo nie wiedziałem, że na tej stronie jest też o nierównościach z
dwiema wartościami bezwzględnymi:
1805
9 lut 20:48
Patryk: Przecież to równanie... Nie patrz na to co przed chwilą napisałem

9 lut 20:51
Rose: czyli dalej mam to w ten sposob rozpisywac?
x∊(−∞,−2)
(−x−2)(−x+2)+(−x−1)(−x+1)=4x+1
9 lut 20:52
Patryk: Połącz to co mówi Abey i nie rozwiązuj dla niepotrzebnych przedziałów
9 lut 20:52
Abey: Jeżeli nie chcesz chwile pomyśleć, to tak − w ten sposób

9 lut 20:53
Rose: x2−4+x2−1=4x+1
2x2−6=4x
2x2−4x+6=0
9 lut 20:53
Rose: i potem delta
9 lut 20:54
Rose: Δ=16−4*2*6<0
nie ma rozwiazan
itd
a na koniec suma czy czesc wspolna tego wszystkiego?
9 lut 20:55
Patryk: Abey, dlatego na początku napisałem, że pewnie jest szybszy sposób

| | 1 | |
nie ma rozwiązań, bo potwierdza się to co napisał Abey, że x≥− |
| |
| | 4 | |
9 lut 20:56
Patryk: Część wspólna na dany przedział, a rozwiązanie końcowe, to suma ze wszystkich rozwiązań.
9 lut 20:57
Rose: no tak
ale cos na tej zasadzie dla pozostalych tak?
9 lut 20:57
Patryk: Tak
9 lut 21:01
Abey: Patryk, spodziewam się, że jest jeszcze szybszy sposób, ale nie mam pomysłu

Ewentualnie można zauważyć (a raczej rozpisać nierówność trójkąta), że
|x
2−4| + |x
2−1| ≥ 3, wtedy możemy ograniczyć szukanie rozwiązań do przedziału <1;
∞).
9 lut 21:02
Patryk: 3 przedziały i tak wyglądają lepiej, niż 5

A te 3, to już tak długo się nie robi

9 lut 21:09
Rose: co to nierownosc trojkata?
9 lut 21:13
9 lut 21:16
9 lut 21:17
9 lut 21:18


 jak rozwiazac:
|x2−4|+|x2−1|=4x+1
jak rozwiazac:
|x2−4|+|x2−1|=4x+1 



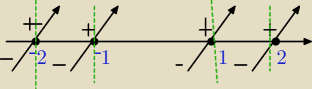 x−2≥0 ⇒ x≥2
x+2≥0 ⇒ x≥−2
x−1≥0 ⇒ x≥1
x+1≥0 ⇒ x≥−1
Czyli przedziały:
1. (−∞,−2)
2. <−2,−1)
3. <−1,1)
4. <1,2)
5. <2,+∞)
x−2≥0 ⇒ x≥2
x+2≥0 ⇒ x≥−2
x−1≥0 ⇒ x≥1
x+1≥0 ⇒ x≥−1
Czyli przedziały:
1. (−∞,−2)
2. <−2,−1)
3. <−1,1)
4. <1,2)
5. <2,+∞)
 Patryk
Patryk



 Ewentualnie można zauważyć (a raczej rozpisać nierówność trójkąta), że
|x2−4| + |x2−1| ≥ 3, wtedy możemy ograniczyć szukanie rozwiązań do przedziału <1;∞).
Ewentualnie można zauważyć (a raczej rozpisać nierówność trójkąta), że
|x2−4| + |x2−1| ≥ 3, wtedy możemy ograniczyć szukanie rozwiązań do przedziału <1;∞).
 A te 3, to już tak długo się nie robi
A te 3, to już tak długo się nie robi 