okrąg i trapez Tynka: W trapez równoramienny o podstawach 2 i 8 można wpisać okrąg. Oblicz odległość między środkami okręgu opisanego na trapezie i okręgu wpisanego w ten trapez.

:): https://matematykaszkolna.pl/forum/16155.html

:): https://matematykaszkolna.pl/forum/17397.html

Tynka: nadal mało rozumiem :<

panpawel: no jak się zastanowiłeś/aś minutę to ja się nie dziwię

Martiminiano: Gdybym to ja umiał rysować tutaj. W każdym razie w czworokąt możemy wpisać okrąg, gdy sumy jego przeciwległych boków są równe. Więc 2+8=2x, gdzie x jest ramieniem trapezu. Ramię trapezu ma długość 5. Wysokość trapezu ma długość 4 (z tw. Pitagorasa). A promień tego możesz sobie policzyć choćby z tego wzoru https://matematykaszkolna.pl/strona/874.html, więc ma on 2. Teraz coś z tym opisanym.

Martiminiano:

	4
Dobra, teraz policzę sinus kąta między ramieniem, a dłuższą podstawą. Więc sinα=		.
	5

	d
Długość przekątnej: 42+52=d2 d=√41 I teraz twierdzenie sinusów: 2R=
	sinα

Martiminiano:

	5√41
R=
	8

Martiminiano: Dalej już dasz radę dokończyć, bo ja muszę uciekać Tu masz podpowiedź: https://matematykaszkolna.pl/forum/259234.html

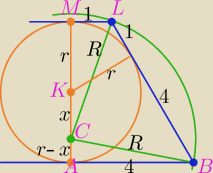
Bogdan: szkic: r = √1*4 = 2 W trójkącie CAB: (r − x)² + 4² = R² W trójkącie CLM: (r + x)² + 1² = R² (2 − x)² + 16 = (2 + x)² + 1 ⇒ 4 − 4x + x² + 16 = 4 + 4x + x² + 1 ⇒ x = ...