trapez równoramienny wpisany w okrąg Krzysiek2: Podstawy trapezu równoramiennego mają długosci 3 i 5, a jego ramie ma długosc 2. Oblicz promien okregu opisanego na tym trapezie. Nigdzie nie mogę znaleźć żadnych wzorów które odnosiłyby się do długości promienia okręgu opisanego/wpisanego w czworokąt.

M.: promien okregu opisanego na wielokacie(czworokacie) : a√3 R=−−−−− 3 wpisanego w wielokat(czworokat) a√3 r=−−−− 6

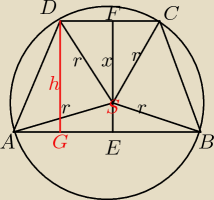
joanna: AG=1cm bo trapez róanoramienny z tw Pitagorasa dla trójkąta AGD AG²+GD²=AD² 1²+h²=2² stąd h=√3 Zatem EF=√3 skoro FS=x to SE=√3−x zauważmy że AE=2,5 DF = 1,5 z Pitagorasa dla trójkąta AES : (1) 2,5²+(√3−x)²=r² zaś dla trójkąta SFD: (2) x²+1,5²=r² z (1) i (2) ponieważ prawe strony są równe (r²) to lewe też: 2,5²+(√3−x)²=x²+1,5² 6,25+3−2√3x+x²=x²+1,25 2√3x=8

	4√3
stąd x=
	3

joanna: do M: a co to jest a w tych wzorach

M.: sama sie zastanawialam. w tablicach matematycznych mam ten wzor a kolega prosil o wzory wiec nap ...

Darek: to wzroy na promien okrega opisango i wpisanego ale na trojkacie rownobocznym

Krzysiek2: W mojej książce pisze tak: "Środek okręgu opisanego na wielokącie leży na przecięciu symetralnych boków wielokąta" , twierdzą też, że środek okręgu WPISANEGO to przeciecie dwusiecznych. To ja już nie wiem co jest prawda, bo Ty zrobiłaś na odwrót i ładnie wychodzi

M.: tu pisze jak woł w czworakacie zeskanowac wam ?

M.: osz cholera.... hahaha faktycznie moj blad ale na czworakat sa a√2//2 i a//2

Krzysiek2: chyba chodzi o kwadrat a nie ogólnie czworokąta

Krzysiek2: Rysunek zrobiony przez Joanne jest zły, ponieważ na pewno środek okręgu opisanego na wielokącie to punkt przecięcia symetralnych wielokąta. W tym wypadku środek będzie leżał poza trapezem. Tylko nie wiem jak tam cokolwiek policzyć

joanna: nie rozumiem Krzysiek 2

joanna: moim zdaniem jest ok

joanna: a wielokąt nie ma symetralnych najwyżej jego boki

joanna: do M chyba tylko dla kwadratu

Krzysiek2: Czepiasz się słówek a nie widzisz swojego błędu w rozumowaniu, zobacz sobie chociazby tutaj: http://pl.wikipedia.org/wiki/Okrąg_opisany_na_wielokącie jest napisane jak byk, że środek okręgu opisanego na wielokącie to punkt przecięcia symetralnych boku tego wielokąta, więc jakim cudem Twoje rozwiązanie może być dobre, skoro Ty wzięłaś dwusieczne kątów?

p: tak powinien mniej więcej wyglądać rysunek

Mickej : Co do Wikipedii to ja bym nie ufał wszystkiemu co tam pisze bo to piszą zwykli ludzie którzy robią błędy częściej niż ja............ to zadanko już ostatnio mnie zaciekawiło więc sam mu się przyglądne

♊:

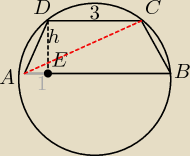
	abc
Wzór na promień okręgu opisanego na trójkącie dowolnym to R=
	4P

Wystarczy znaleźć długość odcinka |AC| i podstawić do wzoru wartości z trójkąta ABC (jak ktoś mi nie ufa, że to bedzie prawda to może zrobić tak dla trójkątów ABC ACD ABD BCD).

Mickej : wow numer 2 znowu mnie zaskoczył

♊: Przecież zawsze powtarzam, ze w geometrii trzeba szukać trójkątów :p

Krzysiek2: w moim podręczniku pisze to samo, tylko, że do mojego podręcznika nie mam linka żeby pokazać. P wykonał dobry rysunek. Ja nie umiem na tym forum rysować, więc może wytłumacze na co wpadłem: oznaczmy rysunek P po kolei oznaczając od lewej − dolna podstawa − A,B, górna podstawa D,C. Ja zrobiłem tak, że narysowałem odcinki r z końcami w punktach A i C i teraz można wywnioskować, że kąt AOC=2*ABC, bo są oparte na tym samym łuku. ABC=60 stopni, więc AOC=120stopni. Przekątna trapezu ma √19, więc mamy trójkąt AOC i długość boku AC=√19 oraz kąt AOC=120 stopni, nie wiem co z tym zrobić.

Krzysiek2: Numerze dwa, nie wiem co nam da promien okręgu opisanego na trójącie, skoro to nie będzie ten sam promień co dla tego trapezu.

Krzysiek2: kurde, w sumie to prawda, że promień będzie taki sam dla trapeza i trójkąta z którego jest złożony... ale mój sposób też dobry, nie?

♊: Krzysiek2 (@ 12 maj 12:30) − czyli taki rysunek co ja zrobiłem Ja widze 1 sposów − masz trójkąt AOC: |AC| = √19, |AO| = |CO| = R Wzory na pole trójkąta jakie znasz ? Polecam przyrównać wzór herona do wzoru na pole z tw kosinusów (jeżeli już miałes tw kosinusów) i wyznaczyć R. Krzysiek2 (@ 12 maj 12:33) − ile różnych okręgów możesz opisać na trojkącie? _{Ja się zawsze uczyłem, że tylko 1.} Ile różnych okręgów możesz opisac na czworokącie ? _{Ja się zawsze uczyłem, że maksymalnie 1. Jeżeli 1 * 1 ≠ 1 to faktycznie będą to różne okręgi.}

Mickej : Ja się wypowiem. Po pierwsze numer dwa to tylko ja tak do niego mówię. Po drugie on już podał rozwiązanie a ty masz książkę więc tylko sprawdź

♊: @ Krzysiek2 (12 maj 12:36) Twój sposób też jest dobry, ale musisz znać tw. kosinusów. Ja zawsze szukam rozwiązań, które opierają się na jak najmniejszej znajomości twierdzeń i wzorów − łatwiej jest na takich "podstawowych" własnościach pokazać komuś, kto nie jest zbyt biegły w matematyce jak rozwiązać dane zadanie. @ Mickey − dzięki misiu :* ale sam potrafię obronić swoich racji _{(pokarmowych)} :P

joanna:

	h
sinDAC=
	2

joanna: stąd kątDAC=60stopni

joanna: zatem kątADB=180−60=120

joanna: z twierdzenia cosinusów AC=√19

Krzysiek2: czyli będzie tak: AC²=r²+r²−2*r*r*cos120, czyli

	1
AC2=2r2−2r2*(−		)
	2

AC²=2r²+r²=3r² 19=3r²

	2
6		=r2
	3

	19
r=√
	3

Dobrze?

Krzysiek2:

	√19		√57
popatrzyłem do odpowiedzi i tam wynik jest taki sam, to znaczy		=
	√3		3

nanaaa: Kąt przy podstawie trapezu równoramiennego ma miarę 30stopni. Dłuższa podstawa jest równa 6√3, a ramie ma długość 3. Oblicz promień okręgu opisanego na tym trapezie.