trapez o okrąg
:)))))): W trapez równoramienny wpisano okrąg. Odległość od środka okręgu do punktu przecięcia
przekątnych trapezu ma się do promienia okręgu, jak 5:13. Wyznacz stosunek obwodu trapezu do
długości wpisanego okręgu.
prosze o pomoc
27 maj 20:51
tim: Ja próbuję.
27 maj 21:05
Basia: Pomagam, ale potrwa bo rysuję
27 maj 21:08
Basia: | | √105 | |
Sorry Tim nie wtrącam się. Jakby co mam rozwiązanie.Wyszło mi |
| |
| | 2 | |
27 maj 21:12
tim:
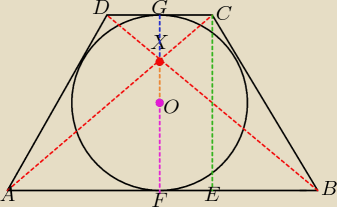
Więc dane:
GO = FO = r
BC = AD = l (Z okazji trójkąta równobocznego)
CD + AB = 2l (Z zależności koła wpisanego w okrąg)
OX = 5x (x jako jakaś proporcja)
GO = FO = r = 13x
FG = 26x
GX = GO − OX = 13x − 5x = 8x
FX = FO + OX = 13x + 5x = 18x
Korzystając z podobieństwa trójkątów DCX oraz ABX, wiemy, że:
CD = 8y (y jako jakaś proporcja)
AB = 18y
CD + AB = 2l
8y + 18y = 2l
AD = BC = l = 13y
Trzeba porównać proporcję x oraz y.
Korzystając z tw. Pitagorasa (trójkąt BCE) oraz mając dane:
CB = 13y
CE = 26x
(26x)
2 + (5y)
2 = (13y)
2
676x
2 + 25y
2 = 169y
2
676x
2 = 144y
2
26x = 12y
Otrzymujesz ostateczne dane:
AD = BC = 13y
AB = 18y
CD = 8y
GO = FO = r = 13x = 6y
Obwód koła = 2πr
Obwód trapezu: AD + BC + AB + CD ...
27 maj 21:18
tim:
Basiu sprawdź, czy gdzieś się nie rąbnąłem.
27 maj 21:20
tim: I co z tym Basiu?
27 maj 21:33
Basia: Strasznie to skomplikowałeś Tim.
XOR =
513
XO =
513R
GX = R−
513R =
8R13
FX = R+
513R =
18R13
s − skala podobieństwa
s =
FXGX =
18R13*
138R =
94
ABCD =
94
AB =
94CD
| | AB−CD | | 94CD−CD | | 54CD | | 5CD | |
BE = |
| = |
| = |
| = |
| |
| | 2 | | 2 | | 2 | | 8 | |
| | AB | | CD | | 9CD | | CD | | 13CD | |
BC = |
| + |
| = |
| + |
| = |
| |
| | 2 | | 2 | | 8 | | 2 | | 8 | |
BE
2 + CE
2 = BC
2
| 25CD2 | | 169CD2 | |
| +4R2 = |
| |
| 64 | | 64 | |
25CD
2+256R
2=169CD
2
144CD
2 = 256R
2
| | 9 | |
AB = |
| *CD = 94*4R3 = 3R |
| | 4 | |
Ob = 2(AB+CD) = 2(3R+
43R) = 2r(
9+43)R =
263R
| Ob | | 263R | | 26 | | 13 | |
| = |
| = |
| = |
| |
| dkoła | | 2πR | | 6π | | 3π | |
ale się nie rąbnąłeś, ja się przedtem rąbnęłam
27 maj 22:08
Bogdan:
Można jeszcze tak:
| k | | 5 | | 13 | |
| = |
| ⇒ R = |
| k i R > 0. |
| R | | 13 | | 5 | |
Trójkąty ABO i CDO są podobne, więc
| R + k | | y | | | | y | | 18 | | y | |
| = |
| ⇒ |
| = |
| ⇒ |
| = |
| |
| R − k | | x | | | | x | | 8 | | x | |
| | 9 | |
y = |
| x, obwód trapezu LT = 4x + 4y = 13x |
| | 4 | |
| | x | | R | | 9 | |
Trójkąty CEO i BEO są podobne, więc |
| = |
| ⇒ R2 = xy ⇒ R2 = |
| x2 |
| | R | | y | | 4 | |
| | 3 | | 3 | |
R = |
| x, długość okręgu LO = 2πR = 2π* |
| x = 3πx. |
| | 2 | | 2 | |
28 maj 01:28
tim: I jak zwykle Bogdan, ze swoim najprostszym rozwiązaniem (oczywiście z podobieństwem
)... xD
28 maj 14:56