pytanko asd: jakie wzory i umiejętności przydadzą się na maturze rozszerzonej a których nie ma w tablicach? wymieniać się spostrzeżeniami

Saizou : wzory redukcyjne

Draghan: Wzory redukcyjne niepotrzebne https://matematykaszkolna.pl/forum/247625.html Ale parę takich "kruczków" było o trójkątach... Np. twierdzenia o dwusiecznej nie ma, tak sądzę przynajmniej. https://matematykaszkolna.pl/strona/498.html Nie ma również wzoru na długość środkowej. Załóżmy, że mamy trójkąt o bokach a, b i c, gdzie kąt α leży naprzeciwko a, kąt β naprzeciwko b, a kąt γ naprzeciwko c.

	1
Długość środkowej, opuszczonej na bok c, to będzie d =		√2a2 + 2b2 − c2
	2

Inną sprawą, której nie ma w tablicach, jest wzór na pole trójkąta, gdy mamy dane jeden bok i wszystkie kąty, np dla znanego boku a:

	1		sinβ * sinγ
P =		a2
	2		sinα

Jeszcze przydatne twierdzenie o wysokości, opuszczonej z kąta prostego w trójkącie prostokątnym, że jej długość jest równa średniej geometrycznej długości odcinków, na jakie podzieliła podstawę. (było to poruszane tutaj: https://matematykaszkolna.pl/forum/246565.html )

zawodus: ostatnie jest w karcie wzorów

muflon: Co do wzoru na pole Δ mając kąty i bok to α leży naprzeciw a

52: jak masz podane wszystkie kąty i jeden bok to twierdzenie sinusów i jest pewne tzn. jak nie pamiętasz dobrze wzorów a to masz w karcie wzorów.

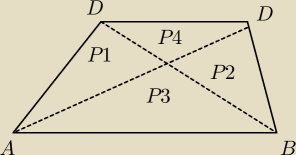
muflon: jest jeszcze chyba takie tw: P1*P2=P4*P3 w dowolnym trapezie, Czy ktoś potwierdzi, że mam rację?

Eta: P(tr)=(√P₃+√P₄)²

Eta: P₃*P₄=P₁² , bo P₁=P₂

Hajtowy: https://matematykaszkolna.pl/forum/247083.html Podstawowa

muflon: Dzięki, a czy to nie jest tak, że jesli w karcie wzorów nie ma wzoru i go używam, to muszę go wykazać?

Draghan: Muflon, odpowiedź na Twoje pytanie z 21.42 brzmi "tak" A ja tam nie wiem dokładnie, co jest zawarte w karcie wzorów, to tak odnośnie wypowiedzi z 21.30 Napisałem tylko to, co sądziłem, że nie ma Tak na wszelki wypadek

Draghan: I chyba nie trzeba tego wykazywać? Twierdzenia Pitagorasa przecież nie trzeba udowadniać... Myślę, że wystarczy komentarz słowny, np. "korzystam ze w wzoru na długość środkowej w trójkącie...".

muflon: btw, ja to nawet nie korzystam z kart, no chyba że trzeba by korzystać z tablic trygonometrycznych , no i zawsze zapominam wzoru na tg kąta między prostymi

muflon: a co Tw Pitagorasa nie ma w kartach? ojej gimby pozapominajo :<

kanoniero: długość środkowej w trójkącie można łatwo wyprowadzić z twierdzenia Carnota

Draghan: Muflon, napisałem, że nie wiem przecież, co jest w tablicach Ale trochę dziwne rozumowanie zdajesz się przedstawiać... Tak, jakby te śmieszne tablice były jakąś Wyrocznią, a wszystko, czego Wyrocznia nie głosi, jest zabronione i trzeba to usprawiedliwiać Przecież sprawdzający nasze matury są ludźmi z odpowiednim wykształceniem i raczej znają te wzory, a skoro rozwiązanie byłoby poprawne, to dlaczego mieliby obcinać punkty? Przecież jest tam gdzieś w "kluczu" napisane, że każde poprawne rozwiązanie, prowadzące do poprawnego wyniku, jest oceniane maksymalną ilością punktów... Więc po co się martwić? Kanoniero − wyprowadzić można, owszem. Również wzór Herona można wyprowadzić z tego twierdzenia, tylko że na maturze szkoda na to czasu

muflon: a tw Carnota to inaczej cosinusów,? Draghan: Nie wiem, nam matematyczka kiedyś tak mówiła, ale fakt faktem musiałby to być idiota, który by nie zaliczył czegoś co jest zrobione twierdzeniami nie tablicowymi a jest dobrze. Tak wg to wydaje mi się, że te zadania są tak maksymalnie analizowane, żeby najłatwiej było je zrobić wzorami z tablic. Btw co to są grafy Vienna? To jest zwykłe przedstawienie rysunkowe zbiorów?

Saizou : to ja do worka dorzucę tw. o średnich śr. kwadratowa≥śr. arytmetyczna ≥ śr. geometryczna≥śr. harmoniczna + odpowiednie założenia

muflon: Arytmetyczna i Geometryczna okej, ale kwadratową i harmoniczną mamy umieć?

Saizou : można ale nie trzeba

Draghan: Tak, tw. Carnota = tw. cosinusów I tak, co do diagramów, to masz rację Łot? XD Saizou, mógłbyś się bardziej rozpisać z tymi średnimi?

ICSP: To ja może troszkę namieszam : http://en.wikipedia.org/wiki/Carnot's_theorem

Saizou : a wujaszek google gryzie ? pełno tego w Internetach np. tutaj http://www.towarzystwo.edu.pl/dokument/bartlomiej_grochal2012.pdf

Draghan: Saizou, skoro wszyscy mieliby korzystać z wyszukiwarki, po co miałoby powstawać jakiekolwiek forum? Po to ktoś założył ten temat, żeby mieć wszystko w kupce, a nie latać po guglach A ja lecę spać Dobranoc

Saizou : ludzie z natury są leniwi, ale najszczęśliwsi są wtedy kiedy są czymś zajęci wiec może warto poszukać w googlach, a po co wszystko dublować itp.

muflon: A może jeszcze to się przyda: Jeśli funkcja jest ciągła na przedziale <a,b> i f(a)<0, f(b)>0 lub f(a)>0, f(b)<0 to funkcja ma conajmniej jedno miejsce zerowe. Chyba jedno z najoczywistszych twierdzeń, zawsze się dziwie po co wg istnieje, skoro to jest takie oczywiste

Maslanek: Twierdzenie Darboux Dowód jest mniej oczywisty

Saizou : muflon to jest własność Darboux ?

muflon: *... miejsce zerowe, w przedziale (a,b) oczywiście, tak Darbuuuu sprawdziłem, u wujaszka!

Saizou : Maslanek wyprzedził moje pytanie

muflon: A no i klasyka: "W pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tanges i cotanges, a w czwartej cosinus"

Saizou : no i "tylko cosinus pożera minus " cos(−x)=cosx (bo funkcja parzysta)

Kanoniero: Sprawdzałem kartę wzorów i nie ma takich rzeczy też jak np. suma sinusów różnych kątów

Maslanek: Raczej suma sinusów pewnych kątów

Maslanek: W nowej zdaje się jest

zombi: Wiele razy powtarzałem, bardzo użyteczne działko: http://pl.wikipedia.org/wiki/Twierdzenie_Stewarta Poza tym do udowodnienia, że środkowe, wysokości, dwusieczne przecinają się w jednym punkcie: http://pl.wikipedia.org/wiki/Twierdzenie_Cevy

Kanoniero: Maslanek całkowicie nie o to chodzi, chodzi mi o coś takiego : sinα + sinβ = ...

Maslanek: No suma sinusów Wydawało mi się,ze w nowej karcie jest . Ale nie ma Ale wzory są proste

Kanoniero: A czy w karcie jest wzór z jednokładności ? Mam na myśli ten na obliczenie x'

Maslanek: http://archiwum.cke.edu.pl/images/stories/Tablice/tablice_matematyczne.pdf Polecam lekturę Owszem jest

zombi: Tak, ale tam jest mowa jedynie o jednokładności, której środkiem jest punkt (0,0).

Maslanek: Rzeczywiście . Zastanawiam się, czy translacja o wektor, tak, żeby punkt jednokładności (a,b) znalazł się w (0,0) załatwiłby sprawę, czy coś po drodze by się zepsuło. Raczej powinno być dobrze

Kanoniero: x' = k(x−a) + a y' = k(x−b) + b chyba o to chodzilo

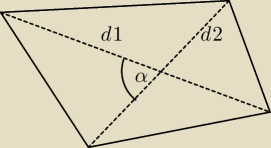
muflon: Pole dowolnego czworokąta= d1d2*sinα*(1/2) +jakby ktoś nie wiedział sinus większego=mniejszego bo razem mają 180 stopni

Draghan: I jeszcze dla czworokątów, na których można opisać okrąg, wzór Brahmaputry (czy jakoś tak ). Taki "rozszerzony" wzór Herona Pole = √p(p−a)(p−b)(p−c)(p−d)

	a+b+c+d
gdzie p =
	2

kris: W ostatnim wzorze jest błąd. Powinno być Pole = √(p−a)(p−b)(p−c)(p−d)