Proszę, kawałek książki, specjalnie dla Ciebie
Cytaty (lekko zmienione przeze mnie, żeby nie pisać niepotrzebności) pochodzą z książki
"MATEMATYKA − kurs przygotowawczy na wyższe uczelnie techniczne", autorstwa R. Leitnera i W.
Żakowskiego (Wydawnictwa Naukowo−Techniczne, wyd. IV niezmienione, 1968).
Ogólne zasady rozwiązywania zadań rachunkowych z geometrii
Przystępując do rozwiązania takiego zadania, należy najpierw przestudiować temat zadania,
wyobrazić sobie figury w nim występujące, wzajemne ich położenie i
naszkicować rysunek.
W przypadku zadań ze stereometrii, oprócz
rysunku perspektywistycznego, pożyteczne są również przekroje bryły.
Następnie należy ustalić, które z występujących w zadaniu wielkości, takich jak
odcinki, pola, czy objętości, są wiadome− ewentualnie co o nich wiadomo, a
która wielkość jest szukaną niewiadomą, której obliczenia żąda temat zadania.
Następnie należy ustalić związki zachodzące pomiędzy wielkościami wiadomymi i
niewiadomymi. Związków tych dostarczą nam odpowiedznie twierdzenia geometryczne i wzory.
Jeśli nie można ustalić bezpośrednich związków między szukaną niewiadomą a wielkościami
wiadomymi, to wprowadzamy pomocniczą niewiadomą, a niekiedy nawet dwie lub więcej. Takimi
niewiadomymi mogą być np. pewne odcinki, które w temacie nie występują, tj. takie, które
nie są ani wiadome, ani nie są szukaną niewiadomą, ale które wiążą się z jednej strony z
wielkościami wiadomymi, a z drugiej z szukaną niewiadomą i pozwolą ułożyć potrzebne nam
równania.
Wprowadzając niewiadome pomocnicze, oznaczmy je dowolnymi literami, przestrzegając,
aby jedna litera nie oznaczała dwóch różnych wielkości.
Kiedy już wprowadziliśmy oznaczenia i przystępujemy do układania równań, to pamiętajmy, że
równań trzeba mieć na ogól tyle, ile jest wszystkich niewiadomych i że muszą to być
równania wzajemnie niezależne. Np. równania a+b = 6 i 2(a+b) = 12 są wzajemnie zależne, bo
jedno wynika z drugiego i nie wnoszą żadnych nowych informacji o wielkościach a i b, tylko
stanowią inne wysłowienie tego samego równania.
Aby znaleźć potrzebne równania, korzystamy z odpowiednich wzorów i twierdzeń
geometrycznych.
Do najczęściej stosowanych, należą:
− twierdzenie Pitagorasa,
− twierdzenia o odcinkach proporcjonalnych, np. tw. Talesa, tw. o dwusiecznej w trójkącie, tw.
o wysokości trójkąta prostokątnego, opuszczonej na przeciwprostokątną (ktoś zna treść
tego twierdzenia? ), tw. o odcinku stycznej i odcinkach siecznych okręgu, przypadki
podobieństwa trójkątów,
− wzory na pola i objętości, np. różne wzory na pole trójkąta.
Dalszych twierdzeń i wzorów, dostarcza trygonometria.
Zastosowania trygonometrii do planimetrii
Przy stosowaniu trygonometrii do rozwiązywania zadań z planimetrii, wskazana jest
następująca kolejność czynności:
− sporządzić szkic,
− oznaczyć odcinki i kąty, występujące w danym zadaniu pojedynczymi literami; ustalić,
które elementy są niezbędne do uzyskania rozwiązania zadania,
− ustalić, jakie trójkąty będą rozważane i które z nich są prostokątne; wybrać
twierdzenia, które będziemy do nich stosować,
− ułożyć równanie, z którego obliczymy niewiadomą − jeśli niewiadomych jest więcej,
powinniśmy mieć tyle równań, ile jest niewiadomych,
− nie wstawiać przedwcześnie danych liczbowych, lecz liczyć jak najdłużej na oznaczeniach
literowych, aby nie stracić ewentualnych okazji uproszczenia otrzymywanych równań lub wyrażeń,
− przed przystąpieniem do obliczeń numerycznych, sprowadzić otrzymany wzór do postaci
najdogodniejszej rachunkowo.
Zestawienie podstawowych przypadków rozwiązywania trójkąta
Wprowadzę taki kontekstowy opis trójkąta:
niech kąt α leży naprzeciw boku a, kąt β − naprzeciw boku b, a kąt γ − naprzeciw boku c.
1. Dane:
bok i dwa kąty
Sposób rozwiązania:
Obliczamy trzeci kąt (ze związku α+β+γ = 180o), potem boki z tw. sinusów. Pole od razu
obliczamy ze wzoru
| 1 | sinβsinγ | 1 | sinαsinγ | 1 | sinαsinβ | |||||||
P = | a2 | = | b2 | = | c2 | |||||||
| 2 | sinα | 2 | sinβ | 2 | sinγ |
| 1 | ||
P= | ab sinγ | |
| 2 |
Może nie są to jakieś nowości dla Ciebie, ale nie
zaszkodzi usystematyzować pewnych wiadomości
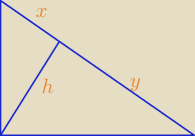Draghan, a propo tego twierdzenia o wysokości padającej na przeciwprostokątną to chyba
chodzi o to:
h2 = xy
Dziękuję, Godzio
Spoko, bezendu Trzeba sobie pomagać
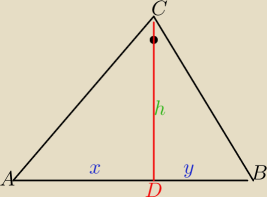Twierdzenie
W trojkacie prostokatnyn wysokosc opuszcona z wierzcholka kata prostego na przciwprostokatna
jest rowna sredniej geometrycznej odcinkow na jakie podzielila przeciwprostokatna
czyli h=√x*y
Te wskazówki są raczej do zadań arytmetycznych z tego działu. Chociaż nadają się również do
dowodów − tylko właśnie trzeba znać twierdzenia
Nie chodzi mi o przepisywanie ich tutaj, ale
może jakieś zdjęcie czy coś takiego. Byłbym mega wdzięczny. Normalnie wysłałbym Ci piwko do
domu 
Ale jedynie do trygonometrii i geometrii były takie krótkie
podsumowania. Reszta cennych informacji zawarta jest w jakich 630 stronach, pachnących kurzem
i milutkim, starym papierem <3
I teraz takie pytanko ode mnie: czy tylko mi się wydaje, czy wzoru na pole trójkąta, gdy dany
jest jeden bok a i wszystkie kąty (α leży naprzeciwko a) w tablicach nie ma
Chodzi o to
| 1 | sinβsinγ | |||
P = | a2 | (i równoważne dla pozostałych boków) | ||
| 2 | sinα |
| a*b*c | ||
i dalej tez wzor z godziny 20:58 = 2R2*sinα*sinβ*sinγ= | = √p(p−a)(p−b)(p−c)=p*r = | |
| 4R |
| α | β | γ | ||||
r2ctg | *ctg | *ctg | to do pola trojkata | |||
| 2 | 2 | 2 |
| 4 | m1+m2+m3 | |||
P= | √p'(p'−m1)(p'−m2)(p'−m3) gdzie p'= | i m1 ,m2 m3 to | ||
| 3 | 2 |
Tak sobie myślę... Wzór z 20:58 można wyprowadzić ze wzoru
| 1 | ||
P = | ab sinγ i twierdzenia sinusów Tylko na maturze szkoda na to czasu Więc może | |
| 2 |
dla Ciebie
Może skoro Eta i Mila nie chcą żebym się odwdzięczył, to może Tobie się jakoś
odwdzięczę za pomoc wszystkim maturzystom?
dla maturzystow
A 
dla tych, którzy pomagają
Wiedzcie, że naprawdę doceniam I może przyjdzie się kiedyś odwdzięczyć
Marcin, co jest? Chłopaki nie płaczą