k.
RS:
Geoemtria Analityczna
Znacie jakieś wzory których nie ma w tablicach a są pomoce w geometrii analitycznej. jakieś
twierdzenia ? (Nie chcę linków z matematyka pisz, bo te wzory wszystkie znam)
27 gru 23:51
28 gru 00:02
RS:
Masz jeszcze coś ?
28 gru 00:03
Lorak: Nie.
28 gru 00:09
tom:
| | x | | y | |
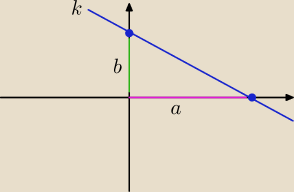
Równanie odcinkowe prostej k: |
| + |
| =1 |
| | a | | b | |
28 gru 00:09
RS: Dzięki za link.
28 gru 00:09
RS:
@Tom równanie odcinkowe ?
28 gru 00:10
ZKZ: Tak −rownanie odcinkowe prostej
Sa tez inne postacie prostych oprocz kierunkowej
28 gru 00:13
RS:
A mogę prosić o przykład zastosowania tej prostej ? Chyba pani w szkole o tym mówiła, ale pewny
nie jestem.
28 gru 00:14
RS: ?
28 gru 00:20
ZKZ: Poczytaj sobie o tej postaci .
Praktyczne zastosowanie jej jest takie ze przedstawia ono prosta przecinajaca
1. Os OX w punkcie x=a
2. Os Oy w punkcie y=b
28 gru 00:24
28 gru 00:27
28 gru 00:30
RS: Dzięki Tom ratujesz moje 100%
28 gru 00:30
28 gru 00:32
ZKZ: Bezendu
28 gru 00:34
tom:
dane proste k∥p
k: Ax+By+C
1=0 i p: Ax+By+C
2=0
| | |C1−C2| | |
odległość "d" między prostymi: d= |
| |
| | √A2+B2 | |
28 gru 00:34
tom:
Co Bezendu ?
28 gru 00:35
RS: ZKZ ?
28 gru 00:37
RS: Pod tym hasłem jakoś nie znalazłem żadnych wzorów.
28 gru 00:38
pigor: ....,
dziwię się, że w polskiej szkole prawie nikt tego nie
pokazuje, tylko "tłucze się " postać kierunkową prostej od gimnazjum
po maturę, tymczasem
| | −ax | | y | |
y= ax+b i a,b≠0 ⇔ −ax+y= b /:b ⇔ |
| + |
| = 1 ⇔ |
| | b | | b | |
| | x | | y | |
⇔ |
| + |
| = 1 , gdzie −ba − odcięta punktu przecięcia |
| | −ba | | b | |
prostej z osia OX (miejsce zerowe funkcji liniowej)
| | x | | y | |
oraz b rzędna punktu przecięcia prostej osią OY ⇔ |
| + |
| = 1. |
| | c | | d | |
28 gru 00:45
tom:
28 gru 00:47
pigor: ..., ups
, tym razem ...przespałem, a tu juz wszystko jasne; przepraszam
28 gru 00:47
tom:
Ejjj
pigorku 
28 gru 00:48
RS:
Dobranoc. I dziękuję !
28 gru 00:51
tom:
28 gru 00:52
RS:
Jutro będę tylko zrobię te swoje 300 zadań
28 gru 00:53
tom:
to prawie ... dywizjon 303
28 gru 00:57
ZKZ: No to masz . Prosta przechodzca przez dany punkt P(x
o,y
o) i prostopadla do danego niezerowego
wektora N = [A,B] ma rownanie A(x−x
o)+B(y−y
o)=0
Teraz skorzystamy z tego wzoru aby sprawdzic jaka prosta przedstawia rownanie
3x+2y−5=0
Sprowadzimy je do tej postaci wyzej laczac wyraz wolny z jednym pozostalych wyrazo np tak
| | 5 | | 5 | |
3x+2(y− |
| )=0 i stad odczytujemy ze jest to prosta przechodzaca przez punkt (0, |
| )i |
| | 2 | | 2 | |
prostopadla do wektora [3,2]
28 gru 00:57
RS:
Chyba tylko dużą ilością zadań da się wykręcić 100%
28 gru 00:59
tom:
Tak, tak trzymaj! .... "trening czyni .... mistrza"
28 gru 01:00