Postać odcinkowa prostej Math: Cześć! Mam pytanie, jak wyprowadzić postać odcinkową prostej. Mógłby ktoś pokazać krok po po kroku? Proszę

pigor: ... np. tak : znana jest ci postać kierunkowa prostej y=a₁x+b , to

	a1x		y
a1x+b= y ⇔ a1x−y= −b / : (−b) ⇔		+		= 1 ⇔
	−b		b

	x		y		x		y
⇔		+		= 1 ⇔		+		= 1 − równanie odcinkowe prostej ,
	b   −   a1		b		a		b

gdzie a − odcięta punktu przecięcia prostej z osią Ox , czyli punktu (a,0) , także miejsce zerowe funkcji liniowej w postaci kierunkowej ; b − rzędna punktu przecięcia prostej z osią Oy, czyli punktu (0,b) , wartość funkcji liniowej w zerze , a także wyraz wolny w równaniu kierunkowym prostej . ...

Math: Aaa, ok! Dzięki, bo jak szukałem, to mnie zastanawiało, czy np A(a,0) to a jest tym samym a, co w y=ax+b. Jednak nie, dzięki!

Stan: Z postaci ogólnej: Ax + By + C = 0 ⇒ Ax + By = −C /:(−C) i C ≠ 0

A		B		x		y
	x +		= 1 ⇒		+		= 1
−C		−C		a		b

A		1		B		1
	=		,		=
−C		a		−C		b

Math: Ok, to pewnie jeszcze ze wzoru na prostą przechodzącą przez dwa punkty też się jakoś da

pigor: ... znam ten − nie tylko twój − problem w rozumieniu tego równania , stąd to moje łopatologiczne wyprowadzenie ; no to powodzenia w stosowaniu tego kapitalnego , ale rzadko − niestety − używanego równania . ...

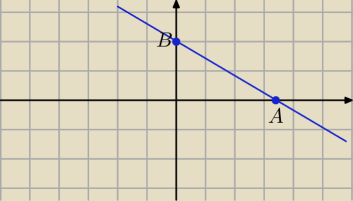
Stan: A(a, 0), B(0, b)

x		y
	+		= 1
a		y