Proszę o pomoc : )) alfa: Dany jest wielomian W(x)=−2x²+10x+8. Wykaż, że wielomian ten ma wszystkie wartości nie większe niż 20,5

Bizon: policz y_w ... dla parabolki smutnej to maximum

alfa: y_w=20,5 , a dalej nie kumam

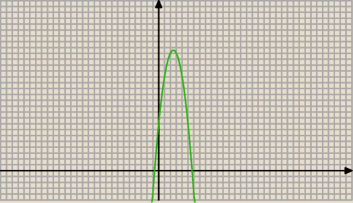
Bizon: ... a teraz? _:)

alfa: y_w=20,5 to max paraboli, a wszystkie inne funkcje sa mniejsze. Kurde no nie ma co sie oszukiwac, nie kumam tego

john: polecam wykuć: https://matematykaszkolna.pl/strona/54.html https://matematykaszkolna.pl/strona/69.html https://matematykaszkolna.pl/strona/79.html

john: Zwróć szczególną uwagę na 3 link Nasza parabola jest smutna, jak napisał Bizon, bo nasze "a" jest ujemne (ramiona w dół). Gdy tak jest, gdzie funkcja osiąga najwyższą wartość (gdzie wykres jest "najwyżej")? W wierzchołku. Stąd szukamy współrzędnych wierzchołka, w zasadzie tylko druga wspołrzędna jest potrzebna

Piotr 10: −2x²+10x+8≤20,5 2x²−10x+12,5≥0 :2 x²−5x+6,25≥0 (x−2,5)²≥0 Dla każdego x∊R jest ta nierówność spełniona. A więc wielomian ten ma wszystkie wartości nie większe niż 20,5

hst: Dziękuję