Równanie Kostek: rozwiąż równanie

	1
cos2x=
	2

	1		1
cox=		lub cosx=−
	√2		√2

cosx=U{1}{√2*U{√2{√2}

	√2
cosx=
	2

	π
cosx=
	4

	π		π
x=		+2kπ lub x=−		+2kπ k∊C
	4		4

	√2
cosx=−
	2

	π
cosx=−
	4

	π
x=π−
	6

	5π		5π
x=		+2kπ lub x=−		+2kπ
	6		6

ok ?

asdf: przed chwila rozwiazywalem Ci zadanie, na bank masz blad, bo:

	5π		√3
cos(		) = −
	6		2

Dominik:

	√2		π
najpierw piszesz, ze cosx =		, a w linijce nizej, ze cosx =		. zdecyduj sie.
	2		4

zapisz to od nowa, bo jest straszny balagan.

Kostek:

	1
cos2x=
	2

	√2		√2
cosx=		lub cosx=−
	2		2

	π
cosx=
	4

	π		π
x=		+2kπ lub x=−		+2kπ
	4		4

	√2
cosx=−
	2

	π
x=−		pytałem o to w inny poście cosinus nie może być ujemny wiec
	4

	π
x=π−		+2kπ
	4

	3π		3π
x=		+2kπ lub x=−		+2kπ
	4		4

teraz ?

asdf: JAK COSINUS NIE MOŻE BYĆ UJEMNY?!

gamer:

	π		π
x =		a nie cosx =
	4		4

Kostek: https://matematykaszkolna.pl/forum/209561.html pierwszy mój post

Kostek: wyszło by mi takie coś

	π
cosx=−
	4

	π		π
x=−		+2kπ lub x=		+2kπ
	4		4

?

asdf: ...jaki pierwszy Twój post, tam nic nie ma takiego. Dostales rozwiazanie do tamtego zadania, teraz wedlug tamtego schematu (lepiej bylo by gdybys to robil ze zrozumieniem) rozwiaz te zadanie.

asdf:

	π		3π
cos(x) < 0, dla x ∊ (		+ 2kπ;		+ 2kπ)...i jak nie moze byc ujemny?
	2		2

Kostek: Tam gdzie cos wyszedł ujemny i to było źle...

Lorak:

	√2		π		π
cosx =		dla x =		+2kπ lub x=−		+2kπ
	2		4		4

	√2
cosx=−		dla x = ....
	2

Kostek: @Lorak

	π
cosx=−
	4

	3π		3π
x=		+2kπ lub x=−		+2kπ
	4		4

Lorak:

	π
coś się uparł na to cosx =−		?
	4

	π
−		to jest argument a nie wartość.
	4

Kostek:

√2		π
	czyli cos450 =>		?
2		4

asdf: można też zauważyć, że:

	√2
cos(x) =
	2

	−√2
cos(x) =
	2

w skrócie:

	π
dla x =		, czyli x = 45o, są 4 rozwiązania, więc powinno być to co 90o, odpowiedź:
	4

	π		kπ
x =		+
	4		2

Kostek: @asdf poczekaj znalazłem rozwiązanie do tego w innej książce zaraz dam zdjęcie

Lorak:

	√2		π
cos45 =		dla x =
	2		4

Kostek: http://www.fotosik.pl/pokaz_obrazek/25813a9620b8739c.html

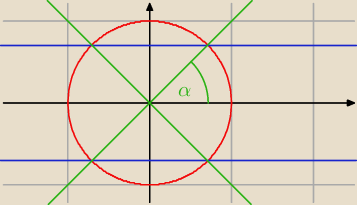
asdf: rysujemy okrąg oraz dwie proste: α = 45^o

	√2
y =
	2

	√2
y = −
	2

	π
x = ±		, czyli ±45o, rysujemy więc funkcje, gdzie wspolczynnik ma kąt 45o, czyli
	4

	π
arctg(x) = ±		⇒ x = 1, x = −1
	4

teraz trzeba narysowac dwie proste: y= 1* x, y = −1*x. Teraz juz mozna wywnioskowac, ze proste

	√2
przecinaja sie pod kątem prostym, teraz weźmy jeden z kątów: np. cos(x) = ±		⇒ x=
	2

	π
		, więc odp:
	4

	kπ		π
x =		+
	2		4

Kostek: @asdf zobacz link tam jest odpowiedź jaką podałem

Lorak: asdf uprościł zapis, Wasze odpowiedzi są równoważne. Rozwiązując równania, w odpowiedziach w podręczniku często spotkasz się z uproszczonym zapisem ( chyba miejsca im szkoda ) przeanalizuj to, a zobaczysz, że Wasze wyniki są równoważne

Kostek: @Lorak widziałeś link tam było własnie do twojego wpisu 21:19

Lorak: widziałem, ale nie kminie "tam było własnie do twojego wpisu 21:19 "

Kostek: czyli moje odpowiedzi są ok ?

Lorak: te z 21:02 są ok

Kostek: tak

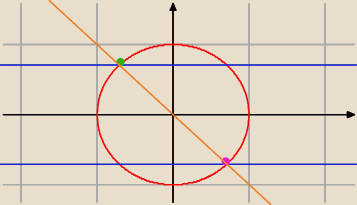
asdf: zobacz, ze te odpowiedzi są równoważne:

3π
	= 90o +45o = 135o
4

	3π		π
−		= 2π −		= 360o − 45o = −45o
	4		4

a przez te punkty przechodzi funkcja y = −x z racji tego, ze teraz bazowałem na liczbach zespolonych (celowo pomijalem te liczby tak, bys Ty to zrozumial), dlatego mam 4 odpowiedzi, a nie dwie. To samo było by, gdybym bazował na y = x

Lorak: co tak? te odpowiedzi z 21:02 są dobre i w tej formie możesz je zostawić. Tylko nad samym zapisem musisz trochę popracować.

Kostek: Już nie dziękuje Panowie za pomoc

Lorak: asdf cenne sposoby, ale wydaje mi się, że najłatwiej zauważyć to bazując na wykresie cosinusa. pozaznaczać tych kilka iksów z odpowiedzi i się zauważy że można uprościć zapis.

Kostek: miało byc już nic , dziękuje Panowie za pomoc @asdf ale tan zapis tez by chyba uznali

asdf: uznali by oba @Lorak Tak, są prostsze rozwiazania,ale nie o to teraz mi chodzilo. Chcialem pokazac, ze to wszystko bazuje po prostu na okręgu, gdzie można to wszystko rozwiązać w inny sposób niż tym wężykiem. Kostek nie musi rozwiazywac kazde zadanie tym samym algorytmem/schematem. Chodzi o to, by potrafil te wszystkie rzeczy ze sobą zgrać. W programowaniu jest podobnie: im więcej sie zna jezykow tym lepiej. Co z tego, ze w pewnym momencie przechodzi sie na jeden jezyk i ignoruje inne, ale znajomosc skladni, czy korzystanie z funkcji, ktorych nie ma w danym jezyku TYLKO pomoga − poszerza umiejetnosci spojrzenia na kolejne problemy i o to w tym wszystkim chodzi . Wydaje mi sie, ze chyba takiego sposobu w szkole sredniej mu nie pokazą, a on juz bedzie wiedziec o co chodzi. Jak trafi na mądrą nauczycielke to jej zaimponuje, jak na glupią − to trudno...uwali ona go, tylko dlatego, ze ONA tego nie umie.

asdf: tutaj też nie ma zapisu + 2kπ...co w pewnym momencie staje sie schematem przy rozwiazywaniu rownosci trygonemtrycznych. Kostek, dla sprawdzenia: rozwiąż: tg(x) = 1

Kostek: Panowie wziąłem to wszystko z książki

	√3
cosx=−
	2

	π
cosx=−
	6

	π		π
x=−		+2kπ Ponieważ po prawej stronie równania mamy liczbę ujemną należy znalezione
	6		6

	π
odjąć od π czyli π−
	6

	π
x=π−		+2kπ
	6

	5π		5π
x=		+2kπ lub x=−		+2kπ
	6		6

Kostek: tgx=1

	π
tgx=
	4

	π
x=		+kπ k∊C
	4

asdf: z tangensem ok, z tym wyzej: sorry, nie chce mi sie juz tego sprawdzac

Saizou :

	1
cos2x=
	2

	√2
lcosxl=
	2

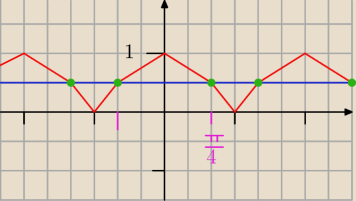
rysuje teraz wykres lcosxl i odczytujemy z wykresu że

	π		π
x=		+kπ lub x=−		+kπ , k∊C
	4		4

Kostek: @asdf to jest z książki przepisane, chciałem tylko pokazać na jakiej podstawie robiłem to zadanie

Lorak: nie wiem dlaczego w ksiażce napisali

	√3
cosx=−
	2

a niżej

	π
cosx=−
	6

Kostek: Też tego nie wiem ja chcę się tylko tego nauczyć

asdf: to źle, staraj sie zrozumiec, w ksiazce sa tez czasem bledy (nie analizowalem). Do puki robisz cos ze zrozumieniem to dobrze

Lorak: daj skan z ksiazki jak możesz tego przykladu cosx = −√3/2

Mila: Kostek, z czym masz problem, w tej liczbie komentarzy trudno mi zorientować się. Napisz.

Kostek: Nie mam skanera, będzie zdjęcie

Kostek: Mila

	1
cos2x=		mam taki przykład
	2

	√2		√2
cosx=		lub cosx=−
	2		2

i teraz rozwiązuje te dwa równania

	√2
10 cosx=
	2

	π		π
x=		+2kπ lub x=−		+2kπ
	4		4

	√2
20 cosx=−
	2

	π
x=−
	4

	π
x=π−		+2kπ
	4

	3π		3π
x=		+2kπ lub x=−		+2kπ k∊C
	4		4

zgadza się ?

Kostek: wracając do tego drugiego

	√2
cosx=−
	2

	π		π
x=−		+2kπ lub x=		+2kπ
	4		4

asdf:

	√2		π
cos(x) =		⇒ x =		+ 2kπ
	2		4

W ogóle nie wyciągasz wniosków...

asdf: sorry, tak miało być:

	√2		π
cos(x) = −		⇒ x =		+ 2kπ
	2

W ogóle nie wyciągasz wniosków...

Kostek: to się zgadza dla jak prawa strona jest dodatnia

Mila: Punkt 1^o w porządku. punkt 2⁰ ja rozwiązuję, korzystając z punktu 1⁰ z serii 2 rozwiązań.

	√2
cos(x)=−
	2

	π		π
x=		+π+2kπ lub x=−		+π+2kπ stąd
	4		4

	5		3
x3=		π+2kπ lub x4=		π+2kπ
	4		4

To jest to samo co u Ciebie.

	−3		5
x4 jak u Ciebie, x =		π+2π=		π=x1
	4		4

Dla sinusa tak

	1
sinx=
	2

	π		π
x=		+2kπ lub x=π−		+2kπ⇔
	6		6

	π		5π
x=		+2kπ lub x=		+2kπ
	6		6

	1
sinx=−
	2

	π		5π
x=		+π+2kπ lub x=		+π+2kπ
	6		6

	7π		11π
x=		+2kπ lub x=		+2kπ
	6		6

Kostek: Mila mam taki przykład

	1
cos(2x+1)=−
	2

	π
2x+1=−
	3

	π
2x+1=π−
	3

	2π		2π
2x+1=		+2kπ lub x=−		+2kπ
	3		3

	2π
2x+1=		+2kπ
	3

	2π
2x=		−1+2kπ /2
	3

	π		1
x=		−		+kπ k∊C
	3		2

lub

	π		1
x=−		−		+kπ k∊C
	3		2

Kostek: ?

Mila: Dobrze.

Kostek: Jeszcze mam jeden problem chyba za mocno mieszam juz to

	π		π
cos(3x+		)=
	2		6

	π		π
3x=		−
	6		2

	π		π
3x=−		+2kπ i teraz mam odejmować π−		jak w poprzednim zadaniu ?
	3		3

	π
3x=π−		+2kπ
	3

	2π		2π
10 3x=		+2kπ lub 20 3x=−		+2kπ
	3		3

2π
	+2kπ/3
3

2π		2π		2π		2π
	+		lub x=−		+
9		3		9		3

asdf:

	π		π		π		π
cos(3x +		) =		⇒ 3x =		−
	2		6		6		2

bzdura... zauważ, że: cos(90−x) = sin(x) Poczytaj o zamianie tych wartości i kofunkcji

asdf: Rób zadania pokolei, jak chcesz to korzystaj z zadan i rozwiazan do nich przygotowanych przez Jakuba: https://matematykaszkolna.pl/strona/2335.html https://matematykaszkolna.pl/strona/1522.html https://matematykaszkolna.pl/strona/1578.html

Kostek: czy zrobić to tak ?

	π		π		π		π
3x=		−		+2kπ lub 3x=−		−		+2kπ
	6		2		6		2

	2π		4π
3x=		+2kπ lub 3x=−		+2kπ
	3		6

	2π		2kπ		2π
x=		+		3x=−		+2kπ /3
	9		3		3

	2π		2kπ
x=		+
	9		3

Kostek: @asdf ja nie rozumiem nic z tych wykresów od Jakuba dlatego staram się sam rozwiązywać zadania najpierw bez przedziału

asdf: ale nie rozumiesz − bo co? bo patrzysz na przyklad 20 minut i wnioskujesz "nie dam rady" Ja przy niektorych rzeczach na studiach musialem siedziec po 2−3 dni bez zadnych efektów, a pozniej wyszlo, ze jest to banalne. Tak samo jak Ty teraz pisalem zadania, dopytywalem, ale i szukalem rozwiazan, probowalem to wszystko polapac, dzieki takim osobom jak Mila, Basia, Trivial, Vixer i wielu innych zdalem egzaminy z matmy, więc do dziela − od podstaw

Kostek: Dokładnie tak jak napisałeś ale możesz popatrzeć na moje rozwiązanie post 23:47 ?

asdf: napisalem Ci przeciez juz, ze to jest bzdura...Nie mozna nagle polaczyc sobie wartosci z argumentami ich do siebie przyrownac (nie w trygonometrii, a jak juz to nie w tym przypadku).

Kostek:

	π		√3
a jak by było cos(3x+		)=		?
	2		2

asdf: to wnioskujesz, ze:

	√3		π
3x =		−
	2		2

asdf: z tabelki, którą Ci podeslalem (napisales, ze ją znasz): cos(90 + x) = −sin(x) i teraz prościej

	−√3
sin(x) =
	2

Kostek:

	√3		π
cos		=
	2		6

π		π
	−
6		2

Mila: Błędny zapis w pierwszej linijce. Chyba masz na myśli, że :

	π		√3
cos(3x+		)=
	2		2

czy

	π		√3
cos(3x+		)=−
	2		2

Kostek: @asdf ja już uciekam dzięki za pomoc jeszcze jutro będę się z tym zmagał

Kostek: Mila to pierwsze

Mila: Godz. 0:0 błędny zapis. Kostek dzisiaj już dobranoc, jutro mogę tłumaczyć, chyba że będzie to robił ASDF, nie mogą dwie osoby naraz, bo będziesz miał mętlik w głowie.

asdf: Mila, jutro z czasem u mnie będzie ciężko, lubie sobie pospac, a pozniej troche programowania, pozostaje wieczorem.....ale w piatek wieczorem (...) jak to w piatek wieczorem

Mila: Kostek załóż nowy wątek, bo tu długo się przewija.