Równania trygonometryczne Kostek:

	√3
cosx=−
	2

	π		π
x=−		+2kπ lub x=		+2kπ k∊C
	6		6

zgadza się ?

Piotr 10: Popatrz na wykres y=cosx jeszcze raz

Kostek: cos nie może być ujemny ? a sinus może ?

Piotr 10:

	√3
−		≈ −0,87
	2

I teraz narysuj sobie prostą y=0,87 tak na oko i zobacz czy się zgadza to co napisałeś

Piotr 10: y=−0,87 minusa zapomniałem napisać

Piotr 10: To co napisałeś by było poprawnie wtedy gdy:

	√3
cosx=
	2

Kostek: w książce ma tak podane cosx=cosx₀ x=x₀+2kπ lub x=−x_o+2kπ k∊C

Piotr 10: Ale nie powinieneś się wg mnie uczyć wzorów, najlepiej z wykresów odczytywać, najpierw naucz się określać te podstawowe równania, tu masz link: https://matematykaszkolna.pl/strona/1578.html ja spadam na losowanie LM

Kostek: czemu jak w cosinus mam ujemny to π−x₀ a w sinusie normalnie wynik zostawiałem ?

Kostek: Nadal nie rozumiem

Kostek: up

Kostek: Potrafi ktoś odpowiedzieć na to pytanie ?

asdf: ostatnia tabelka, warto znac to, szybko rozwiążesz dzieki temu zadanie: http://www-users.mat.umk.pl/~k2011/trygonometria/trygonometria.html

Kostek: Znam tą tabelkę tylko dlaczego jak sinus wychodzi ujemny to jest ok a jak cosinus to robimy π−x_o ?

asdf: nie wiem o co Ci chodzi...

Kostek: To zobacz mój post 17:50... Nie wiesz o co mi chodzi a linki podajesz ?

asdf: Troche kultury czlowieku, bo widze, ze masz wielkie pretensje do ludzi, ze chca Ci pomoc, nara.

Kostek: Sorry ale dajesz mi link w którym mam tabelkę którą znam chodziło mi o to czemu cosinus nie może wyjśc ujemny

asdf:

	−√3
cos(x) =		jest ujemny w drugiej i trzeciej cwiartce, czyli:
	2

	−√3
druga ćwiartka: cos(π−x) =
	2

	−√3
trzecia ćwiartka: cos(π+x) =
	2

	π		√3		π
cos(		) =		, czyli x =
	6		2		6

	π		−√3
cos(π−		) =
	6		2

	5π		−√3
cos(		) =
	6		2

i drugi przypadek:

	π		−√3
cos(π+		) =
	6		2

	7π		−√3
cos(		) =
	6		2

	5π
x0 =		+ 2kπ
	6

	7π
x1 =		+ 2kπ
	6

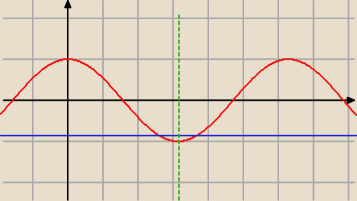
asdf: na wykresie zielona krecha to x = π

Kostek: Dzięki o takie coś mi mniej więcej chodziło