Zadanie Piotr: Dane są liczby a,b,c ∈ R takie, że równanie ax⁴ + bx² + c = 0 ma cztery rozwiązania rzeczywiste x1,x2,x3,x4 . Oblicz wartość wyrażenia |x₁|+ |x₂|+ |x₃|+ |x₄| . Próbowałem wprowadzić zmienna pomocniczą ''t' , ale nic konkretne nie otrzymałem. Wzory Viete'a dla czwartego stopnia też i nic Proszę o pomoc

ciuchcia: ze zmienna pomocniczą "t" powinno pomóc, przynajmniej tak na oko patrząc t = x², t > 0 at² + bt + c = 0 i z tego otrzymujemy pierwiastki: x₁ = √t₁ ∨ x₂ = −√t₁ x₃ = √t₂ ∨ x₂ = −√t₂ podstawiasz pod swoją wartość bezwzględną, już coś widzisz, czy rozpisywać dalej ?

Piotr: A w ten sposób a ja liczyłem deltę po podstawieniu zmiennej pomocniczej

Piotr: To ile ta wartość bedzie wynosic ?

ciuchcia: nie wiem, nie liczyłem podstawiaj pod |x₁| + |x₂| + |x₃| + |x₄| a do czegoś sensownego powinieneś dojść

Piotr: Wlasnie jakos nie potrafie 2(√t₁+√t₂)

ciuchcia: no i w tym momencie wprowadziłbym jakąś zmienną n, i od niej uzależnił wynik (czyli uzależnił od a, b, c, które mamy w poleceniu), wprowadzenie − by nie robić bałaganu i żeby było zgodne zasadą równań

Piotr: Huhu kolejna zmienna , to zadanie ze strony zadania.info ( z matury próbnej). Bardzo ciekawe tam mają zadania

Eta: Dobrze teraz dokończ: W²= 4(t₁+t₂+√t₁*t₂)

	−b
ze wzorów Viete'a t1*t2 =		>0
	a

	c
t1*t2=		>0
	a

	−b		c
podstaw : w2= 4(		+√		)
	a		a

W=...........

ciuchcia: dla Ety ale nie trzeba było chyba rozwiązania pisać

ciuchcia: oczywiście tam W² = 4(t₁ + t₂ + 2√t₁ * t₂)

Piotr: Tak, zaraz to spróbuje dokończyć

Eta: Ajjj no jasne ,że tak Dzięki ciuchcia z poprawkę .......

Piotr: Kurcze jak to dalej rozwiązać? 0 pomysłu..

ciuchcia: Eta napisała ( rozwiązanie praktycznie ) pierwiastkujemy i nie zapominamy o dwójce

Piotr:

	−b		c
W=2√		+√
	a		a

Piotr: Ten pierwiastek pierwszy jest na cale wyrazenie oprocz 2 a ten pierwiastek drugi na c/a

ciuchcia: "prawie" dobrze, pisałem nie zapominamy o dwójce

Eta: Zapisz bardziej "elegancko" Usuń jeszcze niewymierność z mianownika pod pierwiastkiem

ciuchcia: z tą niewymiernością nie taki zły pomysł, bo póki co wygląda to tak jak jajko na garniturze prezydenta

Piotr: Ok. Zaraz poprawię

Eta:

Eta: Dobre porównanie ........ ciuchcia

Piotr: Eta a ta liczba ''2'' w pierwiastku mi bez niej wyszlo. Tak samo wszystko tylko tej dwojki nie mam w pierwiastku

ciuchcia: dziękuję , pracowałem nad metaforami

Eta: w²=(√t₁+√t₂)²= t₁+t₂+ 2√t₁t₂

Eta: Oczywiście jeszcze 4przed ( t₁+t₂+2√t₁t₂)

Piotr: Ok, dziękuję Eta i ciuchcia za pomoc . Trudne te zadanie było

Eta: Eeeetam......... łatwe było

Piotr: Yhym, tak tak. Nie wiem czemu ale deltę liczyłem po podstawieniu t i mi głupoty wychodziły. Eta dla Ciebie każde zadanie ''łatwe''

ciuchcia: bierz się za planimetrię, bądź stereometrię i pamiętaj o świętym wzorze : P(tr) = (√P1 + √P2)²

Piotr: Co to za wzór ? Stereometrii nie mialem jeszcze. A planimetria to w miare moze byc

Eta: ( mój ukochany wzorek i jeszcze taki P_tr= ( k+1)²*P₂ , k skala podob. P₂ = P(ΔDCS)

Piotr: Teraz trygonometrię chce powtórzyć sobie tylko muszę skończyć dział w sumie prosty ''Przeksztalcenia wykresow funkcji''

ciuchcia: zapytaj ciocię Etę

Piotr: Eta co to za wzór ktory podal ciuchcia ?

ciuchcia: nawet nie musisz już pytać dostałeś promocje "3 in 1"

Piotr: Właśnie nie wiem do czego te wzoreczki

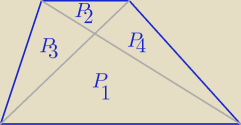
Eta: Oblicz pole trapezu wiedząc ,że P₁= 9 P₂= 4 Oblicz pola P₃ i P₄ = ?

ciuchcia: wykorzystać te wzorki na maturze, to prawie jak otrzymać virtuti militari

Piotr: trojkaty w ktorych sa pola P₃ i P₄ sa podobne ale co dalej hmm ?

Eta: https://matematykaszkolna.pl/forum/191513.html

Eta: https://matematykaszkolna.pl/forum/133835.html

Piotr: Ok, przeanalizuję to dzisiaj wieczorem . Dziękuję

Eta: https://matematykaszkolna.pl/forum/56604.html

Piotr:

Eta: Wpisz w forumową wyszukiwarkę "Eta, trapez" Zobaczysz ile razy ten wzorek był wykorzystywany

Piotr: Właśnie widzę, coś tam mi się obiło o uszy, ale ''wyleciało'' , bo rzadko jakoś używałem tego wzoru do zadań

ciuchcia: dlatego to jest święty wzór, dziwię się, że go w tablicach nie umieszczą (maturalnych rzecz jasna )

Eta: Nie umieszczą? bo myślę, że go nie znają

Piotr: Wolą jak uczniowie na maturze zabłysną i wyprowadzą sami ten piękny wzorek

ciuchcia: bo nie jest schematyczny, pewnie dlatego

pigor: ... . Dane są liczby a,b,c ∈ R takie, że równanie ax$4+bx²+c= 0 ma cztery rozwiązania rzeczywiste x₁,x₂,x₃,x₄. Oblicz wartość wyrażenia |x₁|+ |x₂|+ |x₃|+ |x₄| . −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− dla mnie ciekawe zadanie i aby "włożyć" je do swojego archiwum, to może ja pokażę ... jak w pewnej reklamie np. tak : równanie dwukwadratowe jeżeli ma 4 rozwiązania, to są one parami przeciwne x₁= −x² i x₃= −x₄, a więc jeśli x²=y >0 i y₁+y₂=−^b_a i y₁y₂= ^c_a ⇒ ⇒ |x₁|=|x₂|=√y₁ i |x₂|=|x₃|=√t² ⇒ ⇒ (*) |x₁|+|x₂|+|x₃|+|x₄|= 2(|x₁|+|x₂|₎= 2(√y₁+√y₂)=?, ale √y₁²+√y₁²= −^b_a i √y₁²√y₂²= ^c_a /*2 ⇔ ⇔ √y₁²+√y₁²= −^b_a i 2√y₁√y₂= ²_a√ac /+ stronami ⇒ ⇒ (√y₁+√y₂)²=²_a√ac−^b_a ⇒ √y₁+√y₂=√²_a√ac−^b_a, więc stąd i z (*) mamy |x₁|+|x₂|+|x₃|+|x₄|= 2√²_a√ac−^b_a .

pigor: ...o kurcze , oczywiście tam miało być nie |x₂|=|x₃|=√t² tylko |x₃|=|x₄|=√y₂ ,przepraszam ;