zad *: http://www.zadania.info/3814472 nie potrafię zrozumiec początku tego zad

Eta:

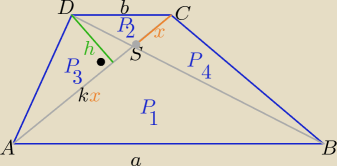
	a
1/ trójkąty ABS i CDS są podobne w skali		=k
	b

to: P₁=k²*P₂ 2/ trójkąty ADS i BCS mają równe pola ( wiesz dlaczego? P₃=P₄

	h*kx		h*x
3/ P3=		i P2=		⇒ P3=k*P2
	2		2

S −− pole trapezu : S= P₁+P₃+P₄+P₂= k²*P₂+2k*P₂+P₂= (k²+2k+1)*P₂

	S
S=(k+1)2*P2 ⇒ P2=
	(k+1)2

	kS
P3=P4=
	(k+1)2

	k2*S
P1=
	(k+1)2

Janek191:

trapez:

przyszłymakler: Mam pytanie. Jak udowodnić, że P₃=P₄? Widzę tam wspólny kąt wierzchołkowy, ale nie wiem jak dalej. Czy na maturze mógłbym zastosować wzór na pole trapezu (√p₁ + √p₂)² bez uzasadnienia?

Adamm: trójkąty ASB oraz DSC są podobne

	1
zastosuj wzór P=		*a*b*sinα
	2

Przyszlymakler: Asb I dsc to oczywiste. Ja pytałem o asd i scb

Adamm: chodzi o boki są podobne z jakąś skalą podobieństwa k pomyśl jeszcze raz

Przyszlymakler: Rozumiem że te boki muszą mieć odpowiednie stosunki jednak chciałbym zobaczyć dowód bo w każdym zadaniu w którym to jest wykorzystywane autor rozwiązania pomija dowód ze P3 i P4 sa przystajace

Adamm: mają taki sam kąt, więc sinα jest taki sam |AS|=k*|CS| |BS|=k*|DS| już widać że mają równe pola

Adamm: jeśli chodzi o dowód, to jest banalnie prosty wystarczy wykazać podobieństwo tamtych dwóch trójkątów, a to że te dwa mają równe pola przychodzi że tak powiem w bonusie dodatkowo, jeśli trójkąt na dole ma pole P to na górze ma k²P oraz dwa boczne mają pola kP

Przyszlymakler: A skąd wiesz że K sa takie same ?

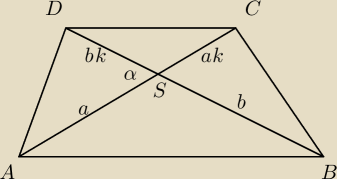
Adamm: trójkąty ASB oraz CSD są podobne na zasadzie kkk w skali podobieństwa k

	1
zatem jeśli oznaczymy PASB=		a*b*sinα (wzór redukcyjny na sinusa)
	2

	1
oraz PASD=PBSC=		*k*a*b*sinα
	2

	1		1
oraz PDSC=		*ka*kb*sinα=		k2*ab*sinα
	2		2

Metis:

Adamm: "zatem jeśli oznaczymy" próbowałem napisać na początku coś innego i zapomniałem usunąć

Adamm: myślę że to powinno rozjaśnić ci wszystkie wątpliwości, i jak sam widzisz to jest banalnie proste

Przyszlymakler: Dziękuję Ci bardzo. A można jeszcze udowodnić że M jest identyczne dla tych odcinków powstałych poprzez miejsce przecięcia−przekatnych?

Adamm: nie rozumiem jakie M? nie wiem co chcesz udowodnić

Przyszlymakler: AC I BD sa podzielone przez na odcinki a ak i b bk. Jak udowodnić że k jest to samo ?

Adamm: przecież to jest własność podobieństwa

Przyszlymakler: Ok nie było.pytania źle spojrzałem na trójkąty. Ogarniam już wszystko. Dzięki Adam

karobert: P3=ABD −P1 P4=ABC −P1 PABD=PABC z tego wynika, że P3=P4

ccc: ΔΔΔΔΔ

popo: (foto stopek) dal cbEBIE SKEBRENKU KOFFFKI <3333333333