| a*h1 | ||
18= | ||
| 2 |
| b*h2 | ||
8= | ||
| 2 |
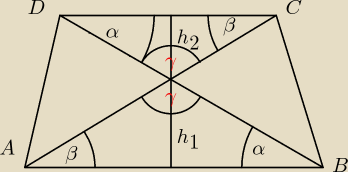 i tyle wiem. Do tych oznaczeń możesz napisać Twoje wskazówki?
i tyle wiem. Do tych oznaczeń możesz napisać Twoje wskazówki?
| |AB|*h1 | ||
18 = | ||
| 2 |
| |DC|*h2 | ||
8 = | ||
| 2 |
| |AB| + |DC| | ||
P = | h | |
| 2 |
 Doszedłem jeszcze do tego, że h1 :h2 = 3:2
Doszedłem jeszcze do tego, że h1 :h2 = 3:2
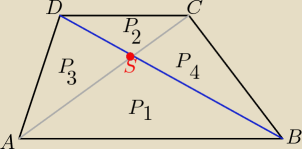 Podaję gotową zależność !
( poszukaj na forum, było podawane wyprowadzenie tej zależności )
P(trapezu ABCD) = ( √P1+ √P2)2 = P1+ 2√P1*P2+P2
P3= P4= √P1*P2
stąd: P(ABCD) = ( √18+√8)2= 18 + 2*√18*8+8= 26+2*√144= 26+ 24= 50
na tym koniec rozwiązania
Odp: P= 50 [j2]
Podaję gotową zależność !
( poszukaj na forum, było podawane wyprowadzenie tej zależności )
P(trapezu ABCD) = ( √P1+ √P2)2 = P1+ 2√P1*P2+P2
P3= P4= √P1*P2
stąd: P(ABCD) = ( √18+√8)2= 18 + 2*√18*8+8= 26+2*√144= 26+ 24= 50
na tym koniec rozwiązania
Odp: P= 50 [j2]

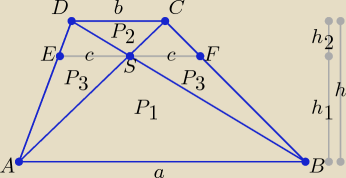 Podam rozwiązanie tego zadania, bo dość trudno jest znaleźć jego rozwiązanie w czeluściach
archiwum naszego forum.
Najpierw wykażemy, że |ES| = |SF| oraz że pola trójkątów ASD i BSC są równe.
Podam rozwiązanie tego zadania, bo dość trudno jest znaleźć jego rozwiązanie w czeluściach
archiwum naszego forum.
Najpierw wykażemy, że |ES| = |SF| oraz że pola trójkątów ASD i BSC są równe.
| a | h | |||
Z podobieństwa trójkątów: ABD i ESD: | = | . | ||
| |ES| | h2 |
| a | h | |||
Z podobieństwa trójkątów: ABC i FSC: | = | |||
| |SF| | h2 |
| 1 | 1 | 1 | 1 | |||||
PASD = | c*h1 + | c*h2 = | c(h1 + h2} = | ch | ||||
| 2 | 2 | 2 | 2 |
| 1 | 1 | 1 | 1 | |||||
PBSC = | c*h1 + | c*h2 = | c(h1 + h2} = | ch | ||||
| 2 | 2 | 2 | 2 |
| 1 | 1 | |||
PASD = PABD − P1 = | ah − P1 i PBSC = PBCD − P2 = | bh − P2 | ||
| 2 | 2 |
| 1 | 1 | |||
PASD = PBSC ⇒ | ah − P1 = | bh − P2 | ||
| 2 | 2 |
| 1 | 1 | 1 | |||
ah − | bh = P1 − P2 ⇒ | h(a − b) = P1 − P2 | |||
| 2 | 2 | 2 |
| 1 | ||
Pole trapezu ABCD PT = | h(a + b) | |
| 2 |
| 1 | 1 | |||
Równania: | h(a − b) = P1 − P2 i | h(a + b) = PT dzielimy stronami. | ||
| 2 | 2 |
| P1 − P2 | |||||||||||
= | ⇒ | |||||||||||
| PT |
| P1 − P2 | ||||||||||||
⇒ | = | ||||||||||||
| PT |
| a | √ P1 | |||
Z podobieństwa trójkątów ABS i CDS: | = | |||
| b | √ P2 |
| P1 − P2 | |||||||||||
= | ||||||||||||
| PT |
| √P1 − √P2 | P1 − P2 | ||
= | |||
| √P1 + √P2 | PT |
| √P1 − √P2 | (√P1 − √P2)*(√P1 + √P2) | ||
= | |||
| √P1 + √P2 | PT |
| 1 | √P1 + √P2 | ||
= | |||
| √P1 + √P2 | PT |
| ab | ||
2. c = | oraz 2c = |EF| jest równe średniej harmonicznej długości podstaw a i b. | |
| a + b |
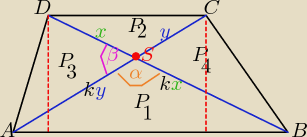 Podam taki dowód dla tej zależności:
ΔABD i ΔABC mają tę samą wysokość i podstawę ( ich pola są równe)
zatem : P1+P3= P1+P4 => P3=P4
z podobieństwa ΔABS ~ ΔCDS
Podam taki dowód dla tej zależności:
ΔABD i ΔABC mają tę samą wysokość i podstawę ( ich pola są równe)
zatem : P1+P3= P1+P4 => P3=P4
z podobieństwa ΔABS ~ ΔCDS
| P1 | √P1 | √P1*P2 | ||||
= k2 => k= | = | |||||
| P2 | √P2 | P2 |
| kx*ky | k2*xy*sinα | |||
P1= | *sinα= | |||
| 2 | 2 |
| 2P1 | ||
to sinα= | ||
| k2xy |
| x*ky | k*xy | 2P1 | P1 | P2 | ||||||
P3= | *sinβ= | * | = | = P1* | ||||||
| 2 | 2 | k2xy | k | √P1*P2 |
| P1*P2 | ||
P3= | = √P1*P2
| |
| √P1*P2 |