FUNKCJA LINIOWA Zasmaczysty: Punkty A=(−4,3) i B=(−1,−2) są wierzchołkami podstawy trójkąta równoramiennego ABC.

	1
Punkt C leży na prostej y=−		x+13. Oblicz współrzędne wierzchołka C.
	2

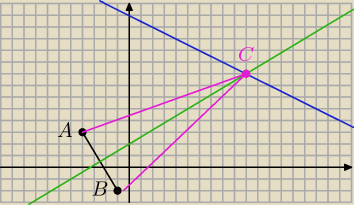
aniabb: C(10,8)

Zasmaczysty: No dzięki, tylko że mogłabyś mi wytłumaczyć jak to zrobiłaś?

aniabb: symetralną odcinka AB i jej przecięcie z daną prosta to C symetralna to prostopadła przechodząca przez środek.. wzory : https://matematykaszkolna.pl/strona/1223.html https://matematykaszkolna.pl/strona/1750.html https://matematykaszkolna.pl/strona/42.html

aniabb: czyli prosta AB to y= −5/3 x− 3²₃ środek AB to E(−2,5 ; −0,5) symetralna EC to y= 3/5 x +2 C(10,8)

Zasmaczysty: Akurat symetralną umiem wyliczać bardziej mi chodziło skąd się wzięła ta niebieska linia.

	yB−yA
I jeszcze mam pytanie do czego jest ten wzór: aAB=
	xB−xA

aniabb: niebieska się wzięła z treści zadania wzór jest na policzenie współczynnika kierunkowego szybciej niż ze wzoru co masz w linku

Zasmaczysty:

	1
aaa to jest ta prosta y=−		x+13 ale skąd wiedziałaś gdzie ją narysować?
	2

aniabb: no przecież jest podany wzór ... podstawiasz kilka iksów i rysujesz..

pigor: ... , analitycznie np. tak: y= −−¹₂x+13 /*2 ⇔ 2y==x+26 ⇔ x=26−2y ⇒ ⇒ (*) C=(x,y)= (26−2y, y)= ? i A=(−4,3) i B=(−1,−2), więc ΔABC równoramienny, to |AC|= |BC| ⇔ AC²= BC² ⇔ (26−2y+4)²+(y−3)²= (26−2y+1)²+(y+2)² ⇔ ⇔ (30−2y)² − (27−2y)²= (y+2)² − (y−3)² ⇔ ⇔ (30−2y−27+2y)* (30−2y+27−2y)= (y+2−y+3)* (y+2+y−3) ⇔ 3(57−4y)= 5(2y−1) ⇔ ⇔ 171−12y= 10y−5 ⇔ 22y= 176 ⇔ y= 8 i z (*) x= 26−16= 10, zatem C= (10,8) − szukany punkt C trójkąta równoramiennego . ...

Zasmaczysty: Rozumiem już wszystko prócz tego jak wyliczyć "symetralną EC"

5-latek : Nasze zadanie aby wyznaczyc symetralna EC sprowadza sie do tego aby wyznaczyc prosta prostopadla do prostej AB i przechodzacej przez punkt E Rownanie prostej AB masz , wsplrzedne punktu E masz wiec wyznacz rownanie prostej EC. Pytanie . Jaki jest warunek aby proste byly prostopadle?.

Zasmaczysty:

	5		2
równanie proste AB: y=−		x−3
	3		3

punkt E: (−2,5;−0,5) aby były prostopadłe a1*a2=−1

	5
−		*a2=−1
	3

	3
a2=
	5

	3
y=		x+b
	5

I tera nie wiem jak wyliczyć to B. Jak próbowałem to mi wyszło że b=−1 a powinno 2

agulka: Symetralna EC jest prostopadła do prostej przechodzącej przez punkty A i B czyli do prosej

	5		11		5		1
y=−		x+		i przechodzi przez punkt E=(−		,		).
	3		3		2		2

	5		11		5
Warunek prostopadłości: a*a1=−1. Dla prostej y=−		x+		a=−
	3		3		3

	5		3		3
Symetralna EC: y=a1x+b, czyli −		*a1=−1⇒a1=		, czyli y=		x+b. Przechodzi ona
	3		5		5

	5		1		1		3		5
przez punkt E=(−		,		), czyli		=		*(−		)+b⇒b=2.
	2		2		2		5		2

	3
Stąd równanie symetralnej EC to y=		x+2.
	5

pigor: .... symetralna EC prostej AB możesz też np. tak : znamy A=(−4,3), B=(−1,−2) i C=(10,8), to AB^→=[−1+4,−2−3]= [3,−5] − wektor normalny symetralnej EC, więc EC : 3(x−10)−5(y−8)=0 ⇔ 3x−5y+10 − szukane równanie EC . ...