wartość bezwzględna bezendu: Mila https://matematykaszkolna.pl/forum/194516.html pamiętasz jak miałem takie zadanie |3x−7|=|5x−9| i napisałem,że można to zrobić (3x−7)²=(5x−9)² to chyba nie do końca to jest dobrze bo powinno być moim zdaniem |3x−7|=|5x−9| 3x−7=5x−9 lub 3x−7=−5x+9 wyniki są takie same jak bym zrobił (3x−7)²=(5x−9)²

moduł: właśnie mam podobny problem, tzn. mam równianie z modułami po obu stronach, postanowiłam podnieść je do kwadratu i dostałam 2 rozw. a w odp jest jedno... https://matematykaszkolna.pl/forum/196463.html

moduł: jak to w końcu jest z tymi modułami?

bezendu: moduł niestety nie umiem Ci pomóc

$$: przenieś moduł na drugą stronę i rozwiązuj przedziałami,..

Eta: |a|=|b| ⇒ a=b v a= −b

$$: nie spamuj, tylko rozwiąż przedziałami..

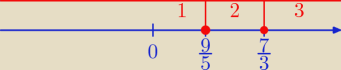
Godzio: Tak jak mówi $$ takie zadania rozwiązujemy w odpowiednich przedziałach:

	9
(−∞,		)
	5

	9		7
<		,		)
	5		3

	7
<		,∞)
	3

bezendu: $$ właśnie chodzi o to żeby nie robić tego przedziałami Eta czyli która wersja jest poprawna 3x−7=5x−9 lub 3x−7=−5x+9 czy to (3x−7)²=(5x−9)² lub (3x−7)²=(−5x+9)²

bezendu: Godzio wiem, że można zrobić to na przedziały ale w zbiorze Andrzeja Kiełbasy był pokazany tez taki sposób

moduł: Godzio, a czy mógłbyś mi jeszcze takie coś rozwiązać, bo muszę się dopiero nauczyć tej metody:

	−x
I		I=−IxI ... albo Ty bezendu, jeśli ją już rozumiesz, to dla ćwiczenia. Bardzo zależy
	x+1

mi na pełnym rozw.

Godzio: Z kwadratami lepiej nie mącić Albo przedziałami, albo tak jak Eta.

Godzio: x ≠ − 1

	−x
|		| = − |x| / * |x + 1|
	x + 1

|−x| = − |x| * |x + 1| ⇒ |x| + |x| * |x + 1| = 0 ⇒ |x|(1 + |x + 1|) = 0 |x| = 0 lub |x + 1| + 1 = 0, ale |x + 1| + 1 > 0 więc sprzeczność, więc rozwiązanie to |x| = 0 ⇒ x = 0

bezendu: czyli wersja pierwsza jak policzyłem to z kwadratami to wyszły mi dwa rozwiązani takie same i zgadzały się z odpowiedzią i właśnie nie rozumiem bo raz jest pokazane, że są kwadraty a raz że ich nie ma

moduł: dalej mi wychodzą dwa rozwiązania...

Godzio: Przez kwadrat może powstać więcej rozwiązań niż jest (ale nie zawsze)

bezendu: hmm właśnie wiem, że może wyjść w rozwiązaniach różna Δ ale do tej pory wychodziły dwa takie same pierwiastki

bezendu: i jak Godzio możesz to usuń post https://matematykaszkolna.pl/forum/196481.html

Eta: Równanie typu |a|=|b| .......... tak jak podałam

bezendu: Eta posiadasz zbiór Andrzeja Kiełbasy

Eta: W czym problem?

bezendu: zobacz jak mam teraz takie coś zadanie 127 maturalne w cz I rozwiąż nierówność |3x−7|≤|5x−9| to muszę zrobić teraz (3x−7)²≤(5x−9)² (3x−7)²−(2x+1)²≤0 (3x−7−2x−1)(3x−7+2x+1)≤0 (x−8)(5x−6)≤0

PW: |a|=|b| ⇔ a²=b² Śmiało można podnosić stronami do kwadratu − dostajemy równanie równoważne. Godzio ma rację, że podnoszenie do kwadratu może wprowadzać "obce"pierwiastki i na ogół nie zaleca się tej metody. Jednak w tym wypadku obie strony (jako moduły) są nieujemne, więc podnoszenie do kwadratu daje równanie równoważne.

bezendu: @PW wiem, że jest to równanie równoważne ale Eta napisała, że poprawnie jest bez kwadratów mam takie coś |2x²−3|=|3x²−7| 2x²−3=3x²−7 lub 2x²−3=−3x+7

PW: Matematycy to ludzie leniwi. Po pierwsze patrzymy, jak sie nie narobić. W tym wypadku bez sensu byłoby podnoszenie do kwadratu (równanie czwartego stopnia). Przy Twoim pierwszym pytaniu podnoszenie do kwadratu było sensowne (zamiast żmudnego "rozbijania na przedziały" mechaniczne rozwiązanie równania kwadratowego).

Eta: @bezendu → https://matematykaszkolna.pl/forum/196452.html

bezendu: ale nie koniecznie muszę podnosić Eta widziałem dziękuję, że poprawiłaś ale jak bym miał x⁴ to mógłbym wprowadzić pomocniczą t=x²