Ciąg geometryczny
bezendu: MIla
Mogłabyś sprawdzić i poprawić ewentualne błędy w zapisie ?
Wyrazy ciągu geometrycznego spełniają następujące warunki
a
1+a
5=68 i a
2+a−6=136. Ile początkowych wyrazów tego ciągu należy dodać, aby otrzymać 2044 ?
a więc robię tak :
a
1+a
1*q
4=68
a
1+q+a
1*q
5=136
a
1(1+q
4)=68
a
1(q+q
5)=136
q+q
5=2+2q
4
q+q
5−2−2q
4=0
q(1+q
4)−2(1+q
4)=0
(q
4+1)(q−2)=0
q=2
a
1(1+2
4)=68
17a
1=68/17
a
1=4
S
n=2044
511=−1+2
n
512=2
n
n=9
24 mar 17:59
Mila:
Dobrze.

Mogłeś łatwiej rozwiązać układ, mniej pisania.
a
1*(1+q
4)=68
a
1q*(1+q
4)=136 dzielę stronami [ a
1q≠0, 1+q
4≠0]
68q=136
q=2
24 mar 18:19
bezendu: ok dziękuje

24 mar 18:20
bezendu: @Mila mam jeszcze kilka pytań do Ciebie

mam takie coś |3x−7|=|5x−9| to muszę to robić na przedziały ?
(3x−7)
2=(5x−9)
2 ?
24 mar 18:28
Mila: Możesz II sposobem.
Ja rozwiązuję przedziałami.
Jeśli znajdę jakieś przeciwwskazania, to Ci napiszę.
24 mar 18:44
bezendu: to jest chyba to równanie równoważne tak ? |a|2=a2 ?
24 mar 18:49
Mila: 
24 mar 18:51
bezendu: bo z tymi przedziałami nie wiem jakie liczby podstawić z przedziału bo jak podstawie np 3 to
wychodzi dodatnie a jak wezmę inną liczbę z przedziału to znowu wychodzi ujemne i robię cały
czas błędy

24 mar 18:55
Saizou :
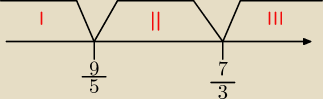
najłatwiej wyznaczyć przedziały przyrównując to co jest w wartości bezwzględnej do 0, czyli
otrzymamy
3x−7=0 5x−9=0
3x=7 5x=9
i w ten sposób powstały 3 przedziały
24 mar 18:58
24 mar 19:01
Saizou : tak i na tych przedziałach się działa

24 mar 19:04
bezendu: tak tylko jak podstawie różne liczby z przedziału to czasami wchodzą różne wyniki

jaka jest
złota metoda na wybieranie tych liczb z środka czy z krańców przedziału ?
24 mar 19:05
Mila: Wybierz kilka równań, to wyjaśnimy wszystko.
24 mar 19:06
bezendu: ok zaraz poszukam
24 mar 19:09
Saizou : weźmy przykład:
|3x−7|=|5x−9|
l3x−7l=−3x+7 bo np. sprawdzamy jaki jest znak dla x=0
l5x−9l=−5x+9 bo np. sprawdzamy jaki jest znak dla x=0
−3x+7=−5x+9
2x=2
| | 9 | |
x=1 i sprawdzamy, czy należy do przedziału x∊(−∞: |
| ) , należy więc Ok |
| | 5 | |
resztę przedziałów analogicznie
24 mar 19:11
bezendu:
taki przykład:
|3x+6|−|3−x|=−1
1) (−∞,−2)
2) <−2,3)
3) <3,∞)
24 mar 19:14
Saizou : przedziały masz dobrze i do dzieła

24 mar 19:16
bezendu:
1) (−
∞,−2)
i tu jest problem |3x+6| podstawię −5 to mam −3x−6
a jak podstawie −1 to mam 3x+6

i sam nie wiem jakie mam podstawiać te liczby
24 mar 19:27
Saizou : ale w przedziale (−∞,−2) nie ma −1

24 mar 19:29
bezendu: a no tak sorry

24 mar 19:29
Mila:
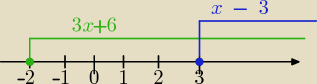
Rozwiązujesz tak:
|3x+6|−|3−x|=−1 zapisuję trochę inaczej
|3x+6|−|x−3|=−1
1) |3x+6|=3x+6⇔3x+6≥0⇔x≥−2 i rysujesz na osi,( wiesz,że w tym przedziale wyrażenie jest
dodatnie)
2) |x−3|=x−3 dla x−3≥0⇔x≥3
a) x<−2
(−3x−6)−(−x+3)=−1
−3x−6+x−3=−1
−2x−9+1=0
−2x=8
x=−4∊ (−
∞,−2)
===========
b) x∊<−2,3)
3x+6−(−x+3)=−1
4x=−4
x=−1
====
c) x≥3
3x+6−x+3=−1
2x=−10
x=−5∉<3,
∞)
odp. x=−1 lub x=−4
24 mar 19:35
Mila:
Przeczytaj uważnie, nic nie trzeba podstawiać, tylko zaznacz na osi , gdzie wyrażenia są
dodatnie.
24 mar 19:36
bezendu: ale ja podstawiałem żeby sprawdzić znak w wartości bezwzględnej zaraz przeczytam dziękuje

24 mar 19:39
bezendu: Rozwiąż równanie
|x|+|x−3|=3
1) (−∞,0)
2) <0,3)
3) <3,∞)
1) −x+(−x+3)=3
−x−x+3=3
−2x=0 / −2
x=0 nie należy do przedziału
2) x−x+3=3
0=0
3) x+x−3=3
2x=6
x=3 jest rozwiązaniem
ale co zrobić z tym drugim przedziałem jak wyszło 0=0 ?
24 mar 20:50
asdf: jest to tożsamość − cały liczony przedział
24 mar 20:53
bezendu: czyli x∊<0,3) ale 3 też wchodzi czyli <0,3> tak ?
24 mar 20:56
asdf:
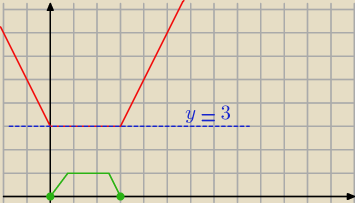
a funkcja wygląda tak + istotny przedział (na zielono)
24 mar 20:56
Mila:
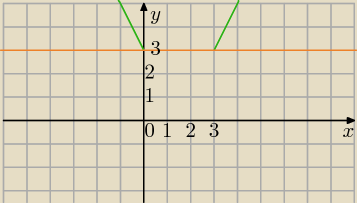
2) Otrzymałeś 0=0 i to jest równość prawdziwa.
Zatem każda liczba x∊<0,3) jest rozwiązaniem równania.
Graficznie ;
f(x)=|x|+|x−3|
y=3
Odp.
x∊<0,3> ( nieskończenie wiele rozwiązań)
24 mar 20:57
bezendu: czyli rozwiązaniem jest <0;3> ?
24 mar 20:58
bezendu: to jeszcze taki przykład
√4x2+20x+25=3x+8=0
|2x+5|=3x+8=0
| | 5 | |
2) < |
| ,∞) takie przedziały ? |
| | 2 | |
24 mar 21:01
asdf: 2x + 5 = 0
3x + 8 = 0
24 mar 21:04
bezendu:
−2x−5=3x+8
−2x−3x=13
−5x=13
2x+5=3x+8
−x=3
x=−3
24 mar 21:17
Mila: A po co tam drugi znak równości? 21:01?
24 mar 21:22
bezendu: |2x+5|+3x+8=0
1) −2x−5+3x+8=0
x+3=0
x=−3
2) 2x+5+3x+8=0
5x=13
5x=−13
czyli roz x=−3 teraz dobrze ?
24 mar 21:28
Mila:
2) piszesz na końcu
| | −13 | | 5 | | −13 | |
x= |
| ∉<− |
| ,∞) ( albo |
| ∉D) |
| | 5 | | 2 | | 5 | |
24 mar 21:40
bezendu:
| | 5 | |
a z pierwszego x=−3∊(−∞,− |
| ) ? |
| | 2 | |
24 mar 21:45
Mila: Tak.
No widzisz jak to ładnie Ci idzie?
24 mar 21:53
Licealista_Theosh: Mila, sprawdzisz moje zadanie? 5min proszę.
24 mar 21:55
bezendu: proste przykłady na razie

24 mar 21:55
Licealista_Theosh: @bezendu masz chwilkę?
24 mar 21:57
bezendu: jak będę CI umiał pomóc to tak

24 mar 22:01
 Mogłeś łatwiej rozwiązać układ, mniej pisania.
a1*(1+q4)=68
a1q*(1+q4)=136 dzielę stronami [ a1q≠0, 1+q4≠0]
Mogłeś łatwiej rozwiązać układ, mniej pisania.
a1*(1+q4)=68
a1q*(1+q4)=136 dzielę stronami [ a1q≠0, 1+q4≠0]

 mam takie coś |3x−7|=|5x−9| to muszę to robić na przedziały ?
(3x−7)2=(5x−9)2 ?
mam takie coś |3x−7|=|5x−9| to muszę to robić na przedziały ?
(3x−7)2=(5x−9)2 ?


 najłatwiej wyznaczyć przedziały przyrównując to co jest w wartości bezwzględnej do 0, czyli
otrzymamy
3x−7=0 5x−9=0
3x=7 5x=9
najłatwiej wyznaczyć przedziały przyrównując to co jest w wartości bezwzględnej do 0, czyli
otrzymamy
3x−7=0 5x−9=0
3x=7 5x=9

 jaka jest
złota metoda na wybieranie tych liczb z środka czy z krańców przedziału ?
jaka jest
złota metoda na wybieranie tych liczb z środka czy z krańców przedziału ?

 i sam nie wiem jakie mam podstawiać te liczby
i sam nie wiem jakie mam podstawiać te liczby


 Rozwiązujesz tak:
|3x+6|−|3−x|=−1 zapisuję trochę inaczej
|3x+6|−|x−3|=−1
1) |3x+6|=3x+6⇔3x+6≥0⇔x≥−2 i rysujesz na osi,( wiesz,że w tym przedziale wyrażenie jest
dodatnie)
2) |x−3|=x−3 dla x−3≥0⇔x≥3
a) x<−2
(−3x−6)−(−x+3)=−1
−3x−6+x−3=−1
−2x−9+1=0
−2x=8
x=−4∊ (−∞,−2)
===========
b) x∊<−2,3)
3x+6−(−x+3)=−1
4x=−4
x=−1
====
c) x≥3
3x+6−x+3=−1
2x=−10
x=−5∉<3,∞)
odp. x=−1 lub x=−4
Rozwiązujesz tak:
|3x+6|−|3−x|=−1 zapisuję trochę inaczej
|3x+6|−|x−3|=−1
1) |3x+6|=3x+6⇔3x+6≥0⇔x≥−2 i rysujesz na osi,( wiesz,że w tym przedziale wyrażenie jest
dodatnie)
2) |x−3|=x−3 dla x−3≥0⇔x≥3
a) x<−2
(−3x−6)−(−x+3)=−1
−3x−6+x−3=−1
−2x−9+1=0
−2x=8
x=−4∊ (−∞,−2)
===========
b) x∊<−2,3)
3x+6−(−x+3)=−1
4x=−4
x=−1
====
c) x≥3
3x+6−x+3=−1
2x=−10
x=−5∉<3,∞)
odp. x=−1 lub x=−4

 a funkcja wygląda tak + istotny przedział (na zielono)
a funkcja wygląda tak + istotny przedział (na zielono)
 2) Otrzymałeś 0=0 i to jest równość prawdziwa.
Zatem każda liczba x∊<0,3) jest rozwiązaniem równania.
Graficznie ;
f(x)=|x|+|x−3|
y=3
Odp.
x∊<0,3> ( nieskończenie wiele rozwiązań)
2) Otrzymałeś 0=0 i to jest równość prawdziwa.
Zatem każda liczba x∊<0,3) jest rozwiązaniem równania.
Graficznie ;
f(x)=|x|+|x−3|
y=3
Odp.
x∊<0,3> ( nieskończenie wiele rozwiązań)

