dowód
technik: Wykaż, że dla każdej liczby całkowitej n liczba n3−n jest podzielna przez 6
i robię tak
n3−n
n(n2−1)
n(n−1)(n+1)
(n−1)n(n+1)
i teraz pytanie jak to sprawdzić czy to jest dobrze ?
i jakie wnioski zapisać ?
19 gru 12:52
krystek: jest podzielna przez dwa i przez 3 ,a więc jest podzielna przez 2*3
19 gru 12:54
technik: wiem, że jak jest podzielna przez 2 i 3 to jest podzielna przez 6 ale skąd mam wiedzieć że to
jest podzielne przez dwa czy trzy mam podkładać jakąś liczbę do sprawdzenia
19 gru 12:55
19 gru 12:56
Eta:
Napisz taki "wierszyk"
n−1, n,n+1 −−− to trzy kolejne liczby całkowite,wśród nich jest co najmniej jedna parzysta
i dokładnie jedna podzielna przez
3
zatem iloczyn takich liczb jest podzielny przez 2 i 3 , czyli taka liczba jest podzielna przez
6
c.n.u
19 gru 12:56
technik: bardzo dziękuje za wierszyk
19 gru 12:57
technik: i za link też
19 gru 12:58
Eta:
I zapamiętaj ten
"wierszyk" , bo często się przydaje do tego typu dowodów
19 gru 12:59
Piotr:
19 gru 13:00
technik: zapamiętam
wcześniej nie robiłem takich zadań więc mam braki
19 gru 13:02
technik: wykaż, że różnica kwadratów dwóch kolejnych liczb nieparzystych jest liczbą podzielną przez 8
2n+1 2n+3 mogą być takie liczby
(2n+1)
2−(2n+3)
2=
=4n
2+4n+1−(4n
2+12n+9)=
=4n
2+4n+1−4n
2−12n−9=
−8n−8 i teraz mam pomnożyć obustronnie przez (−1)
8n+8=8(n+1)
19 gru 13:07
Eta:
@
technika
Dla poćwiczenia
1/ wykaż,że kwadrat liczby naturalnej nieparzystej zmniejszony o
1
jest liczbą podzielną przez
8
2/wykaż,że liczba: 2
2013−2
2009 jest podzielna przez
3
19 gru 13:11
technik: dziękuje Eta
19 gru 13:11
Eta:
Nic nie dzielisz przez (−1) ( bo to nie jest równanie!
liczba podzielna przez 8 jest postaci 8*k, k€C
czyli otrzymałeś : −8(n+1)= 8*k ,bo −n−1€C
co kończy dowód
19 gru 13:15
technik: ok n+3−1 to może byc taka liczba ?
(n+3−1)2=[(n+3)−1]2=n2+6n+9−2n−6+1=n2+4n+4
19 gru 13:19
Eta:
3/ wykaż,że liczba:
| | 8+82+83+..... +82012 | |
|
| jest liczbą całkowitą |
| | 9 | |
4/ wykaż,że liczba:
3+3
2+3
3+... +3
100 jest liczbą parzystą
Wystarczy?
.... czy podać jeszcze parę zadań typu "wykaż liczba"
19 gru 13:21
technik: podać jeszcze a sprawdź to pierwsze jak możesz i masz czas ?
19 gru 13:22
Eta:
Jak zapisujemy liczbę nieparzystą?
19 gru 13:22
technik: np. 2n+1
19 gru 13:24
technik: i ma być pomniejszona o 1 czyli ja zapisałem 2n+3−1
19 gru 13:24
Eta:
ok
to kwadrat tej liczby nieparzystej jak zapiszesz?
19 gru 13:24
Eta:
Kwadrat tej liczby ma być zmniejszony o 1 , a nie liczba zmniejszona o 1 !
19 gru 13:26
technik: (2n−1)2
19 gru 13:26
Eta:
Napisałeś najpierw liczbę 2n+1
to
(2n+1)2 − 1 −−−−− teraz wykaż ,że jest podzielna przez 8
19 gru 13:28
technik: (2n+1−1)(2n+1+1)=2n(2n+2)
19 gru 13:31
Eta:
Rozumiesz zapis: kwadrat liczby nieparzystej pomniejszony o 1
Widzisz to teraz w moim zapisie: z 13:28
19 gru 13:32
technik: czyli to co napisałem o 13:31 jest źle ?
19 gru 13:33
Eta:
Na razie ok
ale to nie jest koniec dowodu
musisz wykazać,że ta liczba jest podzielna przez
8
2n*2*n(n+1) =
4*n(n+1) ( brakuje jeszcze
2 , bo 4*2=8
i nowy "wierszyk " liczby: n, n+1 −−− to kolejne liczby,zatem jedna z nich jest zawsze
parzysta
dokończ komentarz
19 gru 13:36
technik: (2n+1)
2−1=4n
2+4n+1−1=4n
2+4n=4n(n+1)
19 gru 13:37
technik: jeżeli jedna z liczb jest parzysta do dzieli się przez 2 i 4 czyli dzieli się przez 8
19 gru 13:39
Eta:
Poprawiam chochlika, bo napisało mi się o jedno "n" za dużo
tak jak miałeś; 2n(2n+2)= 2*2*n(n+1)=4*n(n+1)
i dodaj teraz komentarz z "wierszyka" z 13:36
19 gru 13:39
Eta:
I
..........
w nagrodę
19 gru 13:40
technik: jeżeli jedna z liczb jest parzysta do dzieli się przez 2 i 4 czyli dzieli się przez 8
19 gru 13:40
technik: dziękuje jeszcze te trzy dowody
mam do Ciebie pytanie czy zapis 13:31 czy ten z 13:37
19 gru 13:41
Eta:
W iloczynie n(n+1) −−− jedna z liczb jest parzysta czyli jest podzielna przez
2
zatem liczba
4*n(n+1) jest podzielna przez 4 i 2 zatem podzielna przez
8
c.n.u
Trzeba opanować te komentarze ( "wierszyki"
19 gru 13:43
technik: no ba jak mam ten zapis 2n(2n+2)= to mogę zapisać 4n2+4 i teraz wyłączyć 4n przed nawias
4n(n+1)
19 gru 13:44
Eta:
Obydwa są dobrze
Na jedno wychodzi:
bo z
13:31 skorzystałeś ze wzoru a
2−b
2
a o
13:37 ze wzoru (a+b)
2
19 gru 13:45
Eta:
Dokładnie tak
19 gru 13:46
Eta:
Pomyśl teraz nad pozostałymi zadaniami, bo ja na chwilę muszę wyjść
19 gru 13:48
technik: ok
19 gru 13:49
Eta:
Jak idzie?
19 gru 14:01
technik: mogę wyciągnąć w tum drugim przed nawias czy nie bardzo ?
19 gru 14:02
Eta:
Jasne
( właśnie o to chodzi
19 gru 14:03
technik: 22009(24+1) ?
19 gru 14:04
Eta:
(24+1) −−− ile to jest?
19 gru 14:05
technik: sorry źle 22009(24−1)
19 gru 14:05
Eta:
Echh tam ma być (24−1)
19 gru 14:06
technik: 24+1=17
19 gru 14:06
technik: poprawiłem zobacz u góry
19 gru 14:06
Eta:
No...
19 gru 14:07
Eta:
24−1=.............
19 gru 14:07
technik: 24−1=15
19 gru 14:08
Eta:
I już będzie ......... "ciepło, ciepło i.... gorąco"
19 gru 14:08
technik: 15 jest podzielne przez 3
19 gru 14:09
Eta:
15= 3*5
zatem liczba ta ma postać: ...........
19 gru 14:09
technik: tak
19 gru 14:10
Eta:
3*5*22009= 3*k , k=5*22009 €C −−− czyli jest podzielna przez 3
19 gru 14:11
technik: teraz ten 3
robię
19 gru 14:12
Eta:
Ok
19 gru 14:12
technik: zawsze trzeba pisać to założenie że k∊C ?
19 gru 14:13
Eta:
Tak
19 gru 14:14
19 gru 14:16
Eta:
zastosuj taki "myk" ( grupowanie po dwa składniki
8+8
2+8
3+8
4+.... +8
2011+8
2012= 8(1+8) +8
3(1+8) +.... +8
2011(1+8)
Widzisz "coś" ?
19 gru 14:21
technik: powtarza się (1+8)
19 gru 14:22
Eta:
1+8 =...........
i wyłącz ją przed nawias ze wszystkich składników i......... zaraz będzie koniec dowodu
19 gru 14:23
19 gru 14:25
Eta:
zad4/ bardzo podobnie ..... już dasz radę
Będę dopiero za 2 h ... powodzenia
19 gru 14:26
technik: ok to sprawdzisz jak będziesz mogła dziękuje za poświęcony czas
19 gru 14:27
Eta:
No i uprość
9 i liczba (8+8
3+.... +8{2011} ) € C i bingo
c.n.u.
19 gru 14:28
technik: 3+3
2+3
3+....3
100
3(1+3)+3
3(1+3)+.....3
99(1+3)
4(3+3
3+.....3
99) ∊C
jeżeli liczba dzieli się przez 4 to jest parzysta
19 gru 14:35
Eta: ok
19 gru 17:21
technik: Eta mam do Ciebie kilka pytań ? i jeden dowód nie wiem jak zrobić
19 gru 17:41
Eta:
Napisz jaki
19 gru 17:41
technik: | | a | | b | |
jeśli liczba a i b są liczbami tego samego znaku to |
| + |
| ≥2 |
| | b | | a | |
19 gru 17:44
technik: | | a | | b | |
to robię tak |
| + |
| −2≥0 |
| | b | | a | |
19 gru 17:45
Eta:
Skoro a i b są tego samego znaku , to iloczyn a*b >0
można nierówność pomnożyć bez zmiany zwrotu nierówności
przez ab
i mamy: a2+b2≥2ab
a2−2ab+b2≥0
(a−b)2≥0 −−− zawsze zachodzi
c.n.u
19 gru 17:49
technik: ok na to nie wpadłem
19 gru 17:52
technik: dziękuje
19 gru 17:54
Eta:
Na zdrowie
19 gru 17:54
technik: | | a | |
czyli jak sprowadzałaś do |
| +{b}{a}≥2 to tak krok po kroku to wyglądało: |
| | b | |
potem do wspólnego mianownika ?
| a*a | | b*b | | 2ab | |
| + |
| − |
| = |
| b*a | | b*a | | a*b | |
19 gru 18:05
Eta:
Następne takie
5/ wykaż,że liczba 4
9+3
9 −− jest podzielna przez:
a)
7
b)
91
6/ Wykaż,że liczba: 4
n+9
n+3
n*2
n+1
jest kwadratem liczby naturalnej
| | n2 | | n3 | | n2 | |
7/ Wykaż,że liczba: |
| + |
| + |
| |
| | 4 | | 2 | | 4 | |
jest kwadratem liczby naturalnej
Powodzenia
19 gru 18:06
Eta:
Tak też może być
19 gru 18:07
technik: sorry głupotę palnąłem
a
2+b
2−2ab≥0 przepraszam
19 gru 18:07
technik: ok zaraz się zabieram do pracy
19 gru 18:08
technik: to trzeba ze wzory skróconego mnożenia w 5 ?
19 gru 18:11
Eta:
5/ tak
a w 7 / i 6/ masz doprowadzić do wzorów na kwadrat liczby
19 gru 18:13
technik: 4
9+3
9=(a
3+b
3)
(4
3)
3+(3
3)
3=(64+27)(4096−1728+729)=91(4096−1728+729) i teraz wierszyk że dzieli się przez
91 bo mam to przed nawiasem i dzieli się przez 7 po 91 jest podzielne na 7
19 gru 18:18
Eta:
ok
mogłeś w tym drugim nawiasie tylko podać,że
(64+27) *(4
6−4
3*3
3+3
6) = 91*k= 7*21*k , k= 4
6−4
3*3
3+3
6 €C
c.n.u
19 gru 18:22
technik:
n
2+2n
3+n
2=2n
3+2n
2=2n
2(n+1)
19 gru 18:23
Eta:
Nie możesz nic dzielić przez 4 ( bo to nie jest równanie !
sprowadź do wspólnego mianownika
19 gru 18:28
technik: ok
19 gru 18:28
technik: | n2 | | 2n3 | | n2 | | n2+2n3+n2 | | 2n3+2n2 | |
| + |
| + |
| = |
| = |
| |
| 4 | | 4 | | 4 | | 4 | | 4 | |
19 gru 18:31
technik: mam jeszcze taka prośbę możesz sprawdzić poprawność zapisu z 18:07
19 gru 18:35
Eta:
z
18: 07
Dobrze, ale jeszcze koniecznie zapisać (a−b)
2≥0 −−− zawsze zachodzi
i c.n.u
z
18:31 −−− niestety ....ale źle
19 gru 18:41
technik: hmm ale całość źle ? sprowadziłem do wspólnego mianownika tak jak mówiłaś
19 gru 18:42
Eta:
A to pewnie dlatego,że wkradł mi się chochlik w zapisie:
powinno być
| | n2 | | n3 | | n4 | |
7/ |
| + |
| + |
| ..... sorry |
| | 4 | | 2 | | 4 | |
19 gru 18:43
Eta:
Popraw i napisz jeszcze raz ...... to sprawdzę
19 gru 18:44
technik: nie ma za co czyli przed tym wszystkim jest 7 tak ?
19 gru 18:45
Eta:
Nie..... zad7/ ...........
19 gru 18:46
technik: a ok
| n2 | | 2n3 | | n4 | | n4+2n3+n2 | | n2(1+2n+n2) | | n2(n+1)2 | |
| + |
| + |
| = |
| = |
| = |
| |
| 4 | | 4 | | 4 | | 4 | | 4 | | 4 | |
19 gru 18:50
technik: n∊N ?
19 gru 18:52
Eta:
ale masz teraz wykazać,że ta liczba jest kwadratem liczby naturalnej
zatem:
| | n(n+1) | |
[ |
| ]2 ponieważ n, n+1 −− kolejne liczby naturalne |
| | 2 | |
to jedna z nich jest parzysta , czyli podzielna przez
2
| | n(n+1) | |
wobec tego liczba [ |
| ]2 = k2 , k€ N |
| | 2 | |
c.n.u
19 gru 18:55
technik: ale w liczniku jest n
2(n+1) a u Ciebie jest n(n+1)
19 gru 18:59
Eta:
Można też dać taki komentarz:
n
2, (n+1)
2 −− kwadraty kolejnych liczb naturalnych
wśród nich jest liczba podzielna przez
4
bo kwadrat liczby parzystej jest liczbą podzielną przez
4
| | n2+(n+1)2 | |
więc liczba |
| = k2, k€N |
| | 4 | |
c.n.u
19 gru 18:59
Eta:
| | n2(n+1)2 | | n(n+1) | |
przecież |
| = [ |
| ]2 |
| | 4 | | 2 | |
19 gru 19:01
technik: muszę poćwiczyć te wierszyki do maja
19 gru 19:01
technik: a no tak bo zwinęłaś w wzór skróconego mnożenia
19 gru 19:02
Eta:
Koniecznie!..... bo takie komentarze musisz zawsze napisać
19 gru 19:02
Eta:
Czekam jeszcze na zad. 6
19 gru 19:04
technik: ok to tu kombinuje coś z potęgami
4
n+9
n+3
n*2
n+1
(2
2)
n+(3
2)
n+3
n*2
n+1
czy pomysł jest trafiony ?
19 gru 19:06
Eta:
8/ wykaż,że dla n€N liczba:
a ) n3+5n jest podzielna przez 6
b) n3−19n jest podzielna przez 3
19 gru 19:09
Eta:
Nie zupełnie, ale ciepło, ciepło
2
n+1= 2
n*2
(2
n)
2 +2*2
n*3
n+(3
n)
2=.....
teraz dokończ.... pamiętaj ,że ma być kwadratem liczby naturalnej
19 gru 19:13
Eta:
Na dzisiaj już Cię nie będę męczyć
Jeszcze tylko dokończ zad, 6/ i zad.8/
19 gru 19:15
technik: 8)
a) n
3+5n=n(n
2+5) każda liczba naturalna podniesiona do
da liczbę parzystą czyli podzielna
przez 2 a druga jest podzielna przez 3
b) n
3−19n
n(n
2−19)=n(n−
√19)(n+
√19)=(n−
√19)n(n+
√19) czyli mamy trzy kolejne liczby naturalne
co druga liczba jest podzielna przez dwa a co trzecia przez 3 czyli dzieli się przez 6 a co za
tym idzie tez przez 3
19 gru 19:17
technik: 6) (2n+3n)2 ?
19 gru 19:19
Eta:
Hehe
czy 3
2=9 −−− jest parzysta?
zad.6/ (2
n+3
n)
2 ( zapewne tak miało być i dopisać,że (2
n+3
n) € N
19 gru 19:24
technik: dobrze ? a w tym a) nie powinno być n
3−5n
19 gru 19:25
technik: ale zapomniałem dopisać że jeśli dodamy do niej +5
19 gru 19:26
Eta:
zad.8/ n
3+5n= n
3−n+6n = n(n
2−1) +
6*n= (n−1)*n*(n+1) +
6*n
i teraz ładny ....... "wierszyk"
b) podobnie .... pokombinuj
19 gru 19:28
technik: wierszyk do a mam trzy kolejne liczby naturalne z czego dwie są podzielne przez 2 i jedna jest
podzielan przez 3 więc jest podzielna przez 6
19 gru 19:30
Eta:
nie "dwie" ... tylko co najmniej dwie !
19 gru 19:31
technik: ok
b) n3−19n=n3−16n−3n=n(n2−16)−3n=(n−4)n(n+4)−3n wierszyk podobny jak w podpunkcie a
19 gru 19:34
Eta:
Nie
n
3−n−18n = ..........
19 gru 19:36
technik: n(n2−1)−18n=n(n−1)(n+1)−18n=(n−1)n(n+1)−18n
19 gru 19:38
Eta:
i dodaj 'wierszyk do pierwszego składnika ... bo drugim jest −3*6*n
19 gru 19:40
technik: czyli mam trzy kolejne liczby naturalne z czego co najmniej dwie są podzielne przez 2 i jedna
jest podzielna przez 3 czyli dzieli się przez 3 ?
19 gru 19:41
Eta:
I co? czy takie dowody są trudne ?
19 gru 19:42
technik: trochę tak bo dopiero teraz zacząłem to robić jeszcze nie znam tych trików np. że n
3−18
rozłożyłaś na n
3−n−18n wiem że powinno tak byc bo inaczej wierszyk nie będzie pasował muszą
byc 3 kolejne liczby naturalne czyli (n−1)n(n+1) i coś tam ale bardzo dziękuje za pomoc i
wytłumaczenie juz mi się coś rozjaśnia
dla Ciebie
19 gru 19:47
Eta:
Tak trzymaj .......... bo "trening czyni mistrza"
Powodzenia
19 gru 19:51
technik: dziękuje jutro liczę na 2 rundę
19 gru 19:52
Eta:
Do usług
Chyba,że jeszcze masz ochotę na jakieś zadanka?
19 gru 19:54
technik: oczywiście że tak a Ty masz czas
19 gru 19:58
Eta:
Napisz zadania ... będę za parę minut (bo idę coś zjeść
19 gru 20:00
technik: ok to smacznego
19 gru 20:01
Saizou : no to może
Wykaż że liczba 3+32+33+...+3998+3999 jest podzielna przez 13
Witaj Eta
19 gru 20:01
Eta:
Pogrupować po trzy wyrazy i po bólu
19 gru 20:02
Kejt: Witaj
Saizou, apetyczne masz zadanko
19 gru 20:03
technik: ok Saizou to teraz Ty będziesz moim nauczycielem
19 gru 20:03
technik: Kejt nie wasz się tknąć tego
19 gru 20:03
Eta:
"pałeczkę" przejmuje
Saizou
19 gru 20:04
Kejt: u..grożą mi
wiesz, że najlepiej smakuje zakazany owoc?
19 gru 20:04
Saizou : wiem że to było proste
Eta nie musiałaś od razu psuć zabawy
Kejt witam
technik ja nie jestem nauczycielem, co najwyżej mogę kogoś wspierać
19 gru 20:05
Eta:
19 gru 20:05
Eta:
.......... idę z tego forum ....
19 gru 20:06
Saizou : to dla
Kejt
| | 3m−5 | |
Wykaż że dla każdego m∊N+ liczba w postaci |
| (m3−3m2+2m) jest liczbą całkowitą |
| | 12 | |
19 gru 20:06
technik: zostań
19 gru 20:07
Eta:
Ale idę ........ coś zjeść
19 gru 20:08
Kejt: to nie fair...on ma fajniejsze
19 gru 20:08
technik: 3(1+3)+3
3(1+3)....+3
998
19 gru 20:09
Saizou : ale to zadanko też jest fajne
19 gru 20:09
Kejt: ja wiem, ja, wybierz mnie!
19 gru 20:09
technik: byłem pierwszy Kejt
3(1+3)+3
2(1+3)+...3{998)(1+3)
19 gru 20:10
Kejt: mam chyba lepszy pomysł
19 gru 20:10
Saizou : no to uzyskamy podzielność przez 4 a ma być podzielne przez 13
kombinuj inaczej
19 gru 20:11
Kejt: haha! przegrałeś.
19 gru 20:12
Saizou : Kejt a jak tam zadanko
19 gru 20:12
Kejt: myślę..
19 gru 20:13
technik: mam druga szanse
19 gru 20:13
technik: dobra Kejt pas ale wytłumacz jak zrobiłaś ?
19 gru 20:15
Saizou : nie ma żadnego pasu
kombinuj jak nie dało się pogrupować po 2 to może po większą ilość ....
19 gru 20:16
Kejt: podpowiedź: ciąg geo.
jak Ci napiszę rozwiązanie to
Saizou mnie zje.
19 gru 20:17
Kejt: nie zrobiłam..to tylko pomysł na rozwiązanie.
19 gru 20:17
technik: w sumie racja
19 gru 20:18
Saizou : Kejt jaki ciąg
nie potrzebnie utrudniasz ale jak chcesz to pokaż ten sposób, bo mi o
inny chodzi
19 gru 20:18
Kejt: czekaj..zaraz pokombinuję..
19 gru 20:20
Saizou : panie
techniku jak idzie
19 gru 20:22
technik: ale nawet jak robię po kilka to nie wychodzi
19 gru 20:23
Saizou : a spróbuj po 3
19 gru 20:24
technik: ok to 3(1+3+32) ?
19 gru 20:26
Saizou : tylko zastosuj to dla każdej trójki
3(1+3+33)+35(1+3+32)+...+3997(1+3+32)
19 gru 20:27
Kejt: dobra, nie chce mi się..za dużo roboty.
19 gru 20:28
technik: a no tak wtedy mam 13(3+3
5+......3
997) i jest podzielne przez 13
19 gru 20:29
Saizou :
+ dopisanie że 3+3
5+...+3
997∊C
19 gru 20:30
technik: a no tak zapomniałem Eta mi mówiła o tym
19 gru 20:32
Saizou : wykaż, że liczba 1010−1 jest podzielne przez 10
19 gru 20:33
technik: ok
19 gru 20:33
Saizou : znaczy się liczba 1110−1
19 gru 20:33
technik: wzór skróconego mnożenia
19 gru 20:36
Saizou : można też zrobić tylko stosowny komentarz
19 gru 20:37
technik: liczba dzieli się przez 10 jak na końcu ma cyfrę 0 ?
19 gru 20:39
Saizou : tak więc co musisz pokazać żeby liczba w postaci 1110−1 była podzielna przez 10
19 gru 20:40
Eta:
Hej ..."nauczycielu"
Mogę napisać ten "stosowny" komentarz ?
19 gru 20:40
Saizou : Eto proszę i nie jestem nauczycielem
19 gru 20:41
Eta:
Poczekamy na
technika
19 gru 20:43
Eta:
I jak z tym zadaniem dla
Kejt ?
Takie łatwe
i pewnie dlatego nie chce się jej podać dowodu
19 gru 20:45
technik: napisałem już komentarz że na końcu będzie cyfra 0 czyli będzie podzielne przez 10
19 gru 20:46
Saizou : ono nie jest trudne tylko trzeba zastosować pewien trick
19 gru 20:46
Eta:
Napisz ten "komentarz" ........ to ocenimy, czy dobry ?
19 gru 20:46
Saizou : a dlaczego na końcu będzie 0
19 gru 20:47
Eta:
ja proponuję taki trik : 3n−5= 3(n−3)+4 ?
19 gru 20:48
Saizou : i właśnie o to mi chodziło
19 gru 20:49
technik: 11
10 to na końcu otrzymam liczby otrzymam cyfrę 1 a jak odejmę to cyfrę 0 czyli podzieli się
przez 10
19 gru 20:49
technik: 1110 miało być
19 gru 20:50
Eta:
@
technika
ok
i masz
19 gru 20:52
technik: dziękuje przyda się na myślenie
dziękuje za dowody
miłego wieczoru
do jutra
19 gru 20:53
Eta:
Miłych snów
19 gru 20:53
Saizou : Liczba 1110 na miejscu jedności ma cyfrę 1, gdy odejmiemy od niej 1 to otrzymamy liczbę z
cyfrą 0 na miejscu jedności, zatem liczba w postaci 1110−1 jest podzielna przez 10
19 gru 20:53
Eta:
A liczba 2011
10 −1 ?
19 gru 20:55
technik: też będzie miała po odjęciu 0
19 gru 20:58
Saizou : Liczba 201110 na miejscu jedności ma cyfrę 1, gdy odejmiemy od niej 1 to otrzymamy liczbę z
cyfrą 0 na miejscu jedności, zatem liczba w postaci 201110−1 jest podzielna przez 10
19 gru 20:58
Eta:
I o to i o to i o to.......
19 gru 20:59
Eta:
Moje
200 
19 gru 20:59
Saizou : Wykaż że jeżeli liczba n jest podzielna przez 3 i nie jest podzielna przez 6 to liczba w
postaci n2+7 jest podzielna przez 8
19 gru 21:02
technik:
19 gru 21:02
technik: ostatni już dowód dziś Saizou
jutro mi jeszcze możesz podrzucić coś
19 gru 21:03
Saizou : jutro nie będę mieć czasu co najwyżej w piątek
19 gru 21:04
technik: ok to może być w piątek
a teraz myślę jak to ugryźć
19 gru 21:05
technik: czyli to ma być jedna liczba ? to jak jest nie podzielna przez 6 to musi być 6 na początku a
jak jest podzielna przez 3 to musi być coś −3 ?
19 gru 21:08
Saizou : nie, zauważ że n można przedstawić jako 3k , k∊C
19 gru 21:10
technik: 6k+3 albo 6k−3 ?
19 gru 21:10
Saizou : n=3k i podstaw do wzoru n2+7
19 gru 21:11
technik: n=6k+3 czy 6k−3 ?
19 gru 21:12
technik: ok
(6k+3)2+7=36k2+36k+9+7=36k2+36+16
19 gru 21:13
Saizou : nie n=3k zatem
(3k)2+7=9k2+7=8k2+8+k2−1
kombinuj dalej
19 gru 21:14
technik: 36k2+36k+16=4(9k2+9k+4)
19 gru 21:15
Saizou : zobacz co napisałem
19 gru 21:16
technik: ok pisałem to zanim Ty napisałeś
19 gru 21:16
Saizou : poprawka do założenia k∊Nieparzystych
19 gru 21:17
Saizou : ja muszę lecieć więc
(3k)2+7=9k2+7=8k2+8+k2−1=8(k2+1)+(k−1)(k+1)
liczby w postaci k−1 i k+1 są dwiema kolejnymi liczbami parzystymi (ponieważ k jest
nieparzyste) zatem ich iloczyn jest podzielny przez 8
19 gru 21:20
technik: 9k2−7 =(3k−√7)(3k+√7)
19 gru 21:20
Eta:
@
technika
Masz dobrze we wpisie
21:15
ciągnij dalej tak:
36k
2+36k +16 = 4*9*k*(k+1) + 16 i teraz "wierszyk"
19 gru 21:26
technik: k k+1 to dwie kolejne liczby naturalne z czego jedna jest parzysta i dzieli się przez 2 czyli
dzieli się przez 8
chyba dziś nie pójdę spać
19 gru 21:35
Eta:
ok
Dobranoc
19 gru 21:37
Eta:
Zobacz ile "nabiliśmy" postów
222
19 gru 21:39
technik: Dobranoc
na kolację jeszcze masz
do zobaczenia jutro
19 gru 21:39
technik: ale wtrąciła się Kejt I Saizou
ale wynik i tak ładny a najważniejsze że już to zaczynam
rozumieć teraz tylko sobie muszę poprzypominać podzielność liczb
19 gru 21:41
19 gru 21:45
Technik: Dziękuje
19 gru 21:48
Eta:
Oooo
co tak "pozieleniałeś" ?
19 gru 21:49
Technik: a tak przed świętami
żeby kolorowo było
zielony to podobnież kolor nadziej i ja mam
nadzieję że będę kiedyś śmigał z matmy tak jak TY
19 gru 21:55
Eta:
19 gru 21:56
Technik: z próbnej podstawy 80 % a z rozszerzenia 20 %
19 gru 21:57
Eta:
Z podstawy b. ładnie
Musisz popracować na rozszerzenie .... na 80%
19 gru 22:16
Technik: właśnie wiem ale czy to się uda ?
funkcje trygonometryczne, wzory redukcyjne zero pojęcia
19 gru 22:28
Technik: Eta masz dłużą chwilkę czasu na
rundę 2
20 gru 14:18
Eta:
Witam
Mam jakąś godzinkę. A co ?
20 gru 14:32
Eta:
Jaki dział na dziś wybierasz?
20 gru 14:35
Technik: no to ciąg dalszy dowodów ?
20 gru 14:36
Eta:
ok
Masz jakieś? czy podać ....
20 gru 14:38
Technik: mam
20 gru 14:39
Technik: wykaż że liczba n
5−n jest podzielna przez 30
20 gru 14:44
Technik: n
5−n = n(n
4−1)=n(n
2−1)(n
2+1)=
=n(n−1)(n+1)(n
2+1)=
= (n−1)n(n+1)(n
2+1)
i teraz wierszyk
20 gru 14:46
ICSP: jaki wierszyk ?
20 gru 14:52
Technik: wierszyk : mam trzy kolejne liczby naturalne z czego co najmniej dwie są podzielne przez
2 i jedna jest podzielna przez 3 więc jest podzielna przez 6 ale jak tu zrobić żeby była
jeszcze przez 5
20 gru 14:54
Technik: ICSP nie jesteś w temacie niestety
20 gru 14:55
ICSP: no to już sobie idę
20 gru 14:56
Technik: wierszyk to ten komentarz do dowodu
powiedz jak to udowodnić lepiej
20 gru 14:57
Eta:
zad.1/ Bez użycia kalkulatora
| | 2012*2013+1 | |
wykaż,że wartość W= |
| jest równa 1 |
| | 20122+2013 | |
zad.2/ Wykaż,że jeżeli liczby: a,b, c są kolejnymi wyrazami ciągu geometrycznego
to zachodzi równość:
(a−b+c)(a+b+c)= a
2+b
2+c
2
20 gru 14:58
Eta:
Do powyższego zadania podpowiem: n
2+1= (n
2−4)+5
20 gru 15:01
Technik: (n2−4)+5=(n2−4+5)(n2−4−5) ?
20 gru 15:02
Eta:
@
Technika .... tylko na maturze nie pisz ,że masz "wierszyk"
( tylko napisz odpowiedni komentarz )
Widzisz,że
ICSP był w szoku: " jaki wierszyk" ?
20 gru 15:04
Technik: ok
zobacz zapis z
15:02 ?
20 gru 15:04
Eta:
, to co napisałeś jest nieprawdą!
Myśl dalej .........
20 gru 15:05
Technik: a już wiem n
2+1=(n
2−4)+5
n
5−n= n(n
4−1)=n(n
2−1)(n
2+1)=n(n−1)(n+1)(n
2−4+5) ?
20 gru 15:08
Eta:
....= n(n−1)(n+1)[(n−2)(n+2) +5]= ......
20 gru 15:10
Technik: teraz to pogrupuje :
(n−2)(n−1)n+5(n+1)(n+2) ? ta 5 dobrze
20 gru 15:14
Eta:
No dobrze ... dokończę, Ty zapamiętaj takie "myki"
po wymnożeniu otrzymujesz:
(n−2)(n−1)n(n+1)(n+2)+
5*n(n−1)(n+1)
w niebieskim składniku masz iloczyn kolejnych pięciu liczb, z których jedna
jest zawsze podzielna przez
5 ( to następny "wierszyk"
Napisz teraz poprawny komentarz, taki by ta liczba była podzielna przez
30
20 gru 15:17
Technik: a w drugim mam kolejne liczby naturalne z czego co najmniej dwie są podzielne przez 2 i jedna
przez 3 więc jest podzielne przez 6 czyli (5*6=30)
20 gru 15:21
Eta:
Na razie muszę odejść od komputera,bo mi się pasztet spali
Myśl teraz nad tymi zadaniami, które Ci podałam 1/ i 2/
20 gru 15:21
Technik: ok
20 gru 15:23
Eta:
20 gru 15:30
Technik: myślę..
20 gru 15:32
Eta:
Nie myśl za długo ... bo na maturze "czas droższy od pieniędzy"
20 gru 15:33
Technik: (a−b+c)(a+b+c)= a
2+b
2+c
2 wzór skróconego mnożenia
20 gru 15:35
Eta:
20 gru 15:36
Technik: to z ciągów trzeba
20 gru 15:36
Eta:
Jaki jest warunek by a,b,c −−− tworzyły ciąg geometryczny?
20 gru 15:37
Technik: an2=an−1*an+1
20 gru 15:39
Eta:
b
2=a*c !
20 gru 15:39
Eta:
Wymnóż lewą stronę i za podstaw za ac= b2 i ........
20 gru 15:41
Technik: tego z tym ciągiem nie zrobię chyba
20 gru 15:41
Eta:
Dawaj
! musisz zrobić
to prostsze niż"budowa cepa"
Ja czekam
20 gru 15:43
Technik: a2+ab+ac−ab−b2−bc+ac+bc+c2=a2−b2−c2+2ac=a2−b2−c2+2b2
20 gru 15:45
Eta:
jeszcze raz ...........
20 gru 15:46
Technik: wiem że nie ma takiego czegoś jak pas
20 gru 15:46
Eta:
Matematyka, to nie zgaduj−zgadula
20 gru 15:47
Eta:
skąd masz tam
−c
2 ?
i ile to jest −b
2+2b
2 =... i zaraz będzie koniec dowodu
20 gru 15:50
Technik: po wymnożeniu (a−b+c)(a+b+c)=a
2−b
2+ac=a
2−ac+ac
20 gru 15:50
Technik: b2
20 gru 15:51
Eta:
Jestem w
.......... mnożyć nie umiesz? ( nie wierzę!
Jeszcze raz na spokojnie przeanalizuj to jak mnożysz
20 gru 15:52
Technik: źle po wymnożeniu a2−b2+ac
20 gru 15:52
Technik: a2−b2+c2
20 gru 15:53
Eta:
L= a2+ab+ac−ab−b2−bc+ac+bc+c2=..........
zredukuj i za ac podstaw b2 i po wszystkim L=P
c.n.u
20 gru 15:55
Technik: a2+2ac−b2+c2 po redukcji =a2+2b2−b2+c2=a2+b2+c2
20 gru 15:58
Eta:
No i ok
Czy to było takie trudne?
20 gru 16:00
Eta:
Na razie
będę za godzinkę .
20 gru 16:01
Technik: nie za szybko mnożyłem i takie farmazony wychodziły ale w końcu wyszło dobrze
20 gru 16:03
Eta:
Dawaj następne .......
20 gru 16:27
Technik: to juz ostatnie dzisiaj to z tą 1
20 gru 16:30
Technik: nic nie skrócę bo w mianowniku mam dodawanie ale można chyba coś wyciągnąć
20 gru 16:34
Eta:
napisz jak myślisz, najwyżej poprawię, podpowiem
20 gru 16:38
Eta:
Dodam,że to bardzo łatwiutkie zadanie
20 gru 16:40
Technik: podzielić to znaczy pomnożyć przez odwrotność
20 gru 16:43
Technik: | | 1 | |
(2012+2013+1)* |
| ? |
| | (20122*2013) | |
20 gru 16:48
Saizou : a jak można zapisać liczbę 2013
20 gru 16:50
Technik: 2000+13 ?
20 gru 16:51
Eta:
| 2012*(2012+1) +1 | |
| = ....... widzisz ? |
| 2012(2012+1) +1 | |
20 gru 16:52
Technik: no i wszystko się "pyknie'' czyli skróci
20 gru 16:54
Eta:
To była "zagadka" jak dla przedszkolaków
20 gru 16:55
Technik: bez przesady
20 gru 16:56
Eta:
Mówimy :
uprości ..... bo "skracać " można np. nogawki u spodni
20 gru 16:56
Technik: ok ok
20 gru 16:57
Eta:
20 gru 16:58
Technik: Eta Twój był 200 i 300 post
20 gru 17:03
Eta:
I "Dywizjon
303"
20 gru 17:06
Technik: Dywizjon był mój
20 gru 17:13
Eta:
Wiem
20 gru 17:14
Saizou : to może taki prosty dowodzik
| | x | | y | |
Wykaż że dla dowolnych dodatnich liczb x i y spełniona jest nierówność |
| + |
| ≥2 |
| | y | | x | |
20 gru 17:22
Technik: ok
20 gru 17:29
ogipierogi: x
2+y
2≥2(xy)
x
2+y
2−2xy≥0
x
2−2xy+y
2≥0
(x−y)
2≥0
c.n.u.
20 gru 17:30
Eta:
20 gru 17:32
Technik:
x
2+y
2−2xy≥0
(x−y)
2≥0
20 gru 17:33
Eta:
20 gru 17:35
Technik:
20 gru 17:38
Eta:
Widzę,że nauka nie poszła w las
.........
20 gru 17:39
Technik: nigdy nie idzie
dziękuje za
20 gru 17:40
Saizou :
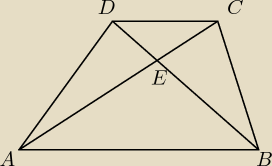
Wykaż że w trapezie ABCD pola trójkątów BCE i ADE są równe
20 gru 17:40
Eta:
zad.3/ Wykaż, że liczba 3n+2−2n+2 −3n−2n , dla n€N
jest liczbą całkowitą
zad.4/ Wykaż,że liczba : 5log37 −7log35 + 3
jest liczbą pierwszą
20 gru 17:43
Technik: na jutro będą zrobione
dzisiaj muszę juz uciekać
20 gru 17:46
20 gru 17:47
Technik: katy w tych trójkątach są takie same:
katy naprzemianległe i kąty wierzchołkowe są takie same czyli trójkąt BCE=ADE ?
21 gru 14:24
Saizou : nie
21 gru 15:23
Technik: jak to nie ?
21 gru 15:38
Saizou :
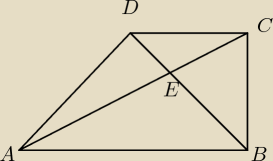
normalnie, a teraz to działa
21 gru 15:45
Technik: nie teraz nie działa
21 gru 15:47
Eta:
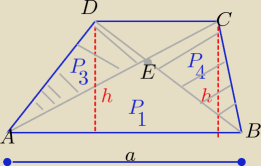
A teraz?............
21 gru 15:59
Technik: teraz muszę lecieć będę potem
21 gru 16:05
Technik: a teraz mam mam kwadrat i dwa trójkąty prostokątne
21 gru 17:00
Piotr: Wykaż, że n, n5, n9, n13..... Mają tą samą liczbę jedności.
Będę wdzięczny.
21 gru 17:37
Piotr: Kombinowałem tak:
1 liczba to n
2 to n*n4
3 to n*n4*n4
....
ale nic mi to nie daje.
Poza faktem stwierdzenia powtarzanego n4
21 gru 17:53
21 gru 17:55
aniabb: Piotr ..na piechotę dla kazdej cyfry
21 gru 17:56
aniabb: jak masz ....1 to każda potęga ....1
jak masz ....2 to .....4 ....8 ....6 ....2 .....4 ....8 ....6 .....2 co 4 się 2
powtarza
itd
21 gru 18:00
Piotr: Niestety nie mam wtyczki, a siedzę na komputerze bibliotecznym i nie mam praw instalacyjnych.
Możesz skopiować rozwiązanie i wstawić?
21 gru 18:01
aniabb: mówiłam na piechotę
cyfra jedności liczby n 0 1 2 3 4 5 6 7 8 9
cyfra jedności liczby n2 0 1 4 9 6 5 6 9 4 1
cyfra jedności liczby n4 0 1 6 1 6 5 6 1 6 1
cyfra jedności liczby n5 0 1 2 3 4 5 6 7 8 9
Widzimy zatem, że w każdym z dziesięciu przypadków, cyfry jedności liczb n oraz n5
są równe. Innymi słowy, liczba n5 −n jest podzielna przez 10.
Stąd wynika, że 10|n4(n5−n), czyli 10|n9−n5. A zatem 10|n4(n9−n5), czyli 10|n13−n9.
Kontynuując to rozumowanie dochodzimy do wniosku, że liczby
n, n5, n9, n13, n17,...
mają jednakowe cyfry jedności.
21 gru 18:18
Piotr: Bardzo dziękuje. Rozwiązanie sensowne i zrozumiałem. n5 to oczywiście n5 tak?
22 gru 20:59
Technik: Eta dalej nie wiem z tym trapezem
a w zadaniu 4 z tymi logarytmami wyszło mi 3 czyli jest
liczbą pierwszą
23 gru 09:58
aniabb: n5 tak
23 gru 10:10
Saizou :
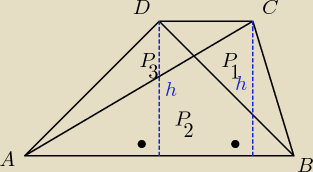
zauważ że
P
ABC=P
ACD
23 gru 11:39
ICSP: Saizou popraw tą bzdurę którą napisałeś.
23 gru 12:00
Technik: Eta jesteś
23 gru 22:47
Eta:
Jeszcze jestem
23 gru 22:49
23 gru 22:52
Eta:
No to na co czekasz?
23 gru 22:54
Technik: Na Ciebie
bo tu z tym trapezem to jest problem ICSP mówi że Saizou napisał bzdurę i już sam
nie wiem co tu jest ok
23 gru 22:55
Eta:
PABC= PABD
23 gru 22:57
Technik: ale czemu znalazł się tu ten prostokąt ?
23 gru 22:58
Eta:
Napisałam wskazówkę (na rys.) 15:59
23 gru 22:59
Technik: jakiś odcinek a tam jest
23 gru 23:00
Eta:
Jaki prostokąt?........narysował wysokości
23 gru 23:00
Technik: no dobra mam wysokości i mam ten odcinek a
23 gru 23:02
Eta:
Echhh
to długość dolnej podstawy i jednocześnie podstawy
trójkątów ABC i ABD i ich wysokości
23 gru 23:02
Technik: ok
23 gru 23:04
Eta:
| | a*h | | a*h | |
P(ΔABD)= |
| i P(ΔABC)= |
| ⇒ P(ΔABC)= P(ΔABD) |
| | 2 | | 2 | |
to: ( z oznaczeń na moim rys.)
P
1+P
3= P
1+P
4 ⇒ .........
i koniec dowodu
23 gru 23:05
Technik: a z tymi logami wyszło mi 3 ale czyli gicior bo liczba 3 jest liczbą pierwszą
idę spać
WESOŁYCH ŚWIĄT i dziękuje za trud włożony w moje męczarnie
23 gru 23:08
Eta:
Miłych snów
23 gru 23:18
Saizou : tak miało być
PABC=PABD
P1+P2=P2+P3
P1=P3
cnu
24 gru 11:19
Ela: Wykaz, ze 22n+11 jest podzielne przez 3
30 wrz 22:54
Jonasz: Ja mam coś takiego:
Wykaż że dla każdej liczby naturalnej n zachodzi 1+3+5+...+(2n−1)=n2
11 lut 22:43
Adamm: Jonasz, nowy temat
11 lut 22:44
Eta:
Suma liczb naturalnych nieparzystych
11 lut 23:12