funkcja sgn
Arnhus: narysuj wykres funkcji y=sgn(x−2)
Fajnie byloby jakby ktos przy rozwiazaniu wyjasnil co to sgn
9 lis 23:51
Artur_z_miasta_Neptuna:
sgn (x) =
−1dla x<0
0 dla x=0
1 dla x>0
innymi słowy
funkcja sqn(x) wskazuje jakiego znaku jest 'x'
9 lis 23:54
Arnhus: a to jak bedzie z (x−2)?
9 lis 23:58
Arnhus: dobra juz wiem
9 lis 23:59
Mila:
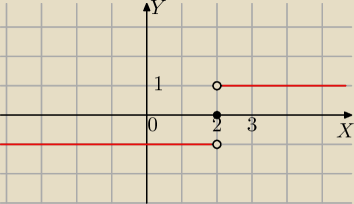
10 lis 00:00
Arnhus: −1 dla x<2
0 dla x=2
1 dla x>2
10 lis 00:00
Arnhus: dzieki za pomoc
10 lis 00:00
Mila: 
10 lis 00:02
Arnhus: mogę was jeszcze o coś prosić?
10 lis 00:09
Mila: Tak.
10 lis 00:10
Arnhus: nie musicie rysowac tylko powiedzcie co z tm zrobic zeby narysowac
10 lis 00:10
Arnhus: x=2 to bedzie miejsce zerowe
10 lis 00:15
Arnhus: y dla x>2 = 1
10 lis 00:16
Arnhus: y dla x<2 =−1
10 lis 00:18
Arnhus: wyznacz miejsce zerowe:
10 lis 00:21
Artur_z_miasta_Neptuna:
Arnhus ... x=2 to nie jest miejsce zerowe ... patrz dziedzina

10 lis 00:28
Artur_z_miasta_Neptuna:
zadanie zaczynasz ZAWSZE od określenia dziedziny (założeń dla 'x')
10 lis 00:28
Arnhus: ? co dziedzina?
10 lis 00:31
Arnhus: nie rozumiem :<
10 lis 00:35
Artur_z_miasta_Neptuna:
jaka jest dziedzina funkcji:
10 lis 00:37
Mila: D dla funkcji z godziny 00:21
3−|x+2|>0
dziedzina dla zadania z oo:10
x−2≠0 ( nie wolno dzielić przez zero)
10 lis 00:40
Arnhus: 0/0≠0 ?
przecież: 0*0=0
10 lis 00:44
Arnhus: dobra, to jak wstaniecie to proszę, określcie mi dziedzinę −[x]+1
10 lis 00:48
Artur_z_miasta_Neptuna:
a od kiedy w mianownku może być 0

10 lis 00:52
Artur_z_miasta_Neptuna:
dziedzina dla −|x| + 1


czy dla −[x] + 1 (czyli część całkowita

)
w dziedzinie ważne jest myślenie ... 'dla jakiego 'x' to wyrażenie nie ma żadnego sensu

'
i tak.
np.:
| coś | |
| nie ma sensu gdy x=0 |
| x | |
√x nie ma sensu dla x<0
log
a x nie ma sensu dla x≤0
log
x a nie ma sensu dla x≤0 i x=1
itd.
10 lis 00:54
Arnhus: [x] jako mantysa
10 lis 00:55
Arnhus: część całkowita
10 lis 00:56
Artur_z_miasta_Neptuna:
jeżeli to nie jest w mianowniku ... pod pierwiastkiem czy inne cudo ... to dziedzina jest R
10 lis 00:57
Arnhus: √x nie ma sensu dla x<0 (?) (zespolone)
10 lis 00:58
Artur_z_miasta_Neptuna:
f(x) = [x]
D
f = R
to [x] ≠ 0 czyli x∉<0;1)
czyli D
f = (−
∞,0) ∪<1;+
∞)
rozumiemy

10 lis 00:58
Artur_z_miasta_Neptuna:
Arnhus ... a miałeś zespolone

10 lis 00:58
Artur_z_miasta_Neptuna:
bo ja Ciebie traktuję jako materiał licealny

jeżeli się mylę − to wybacz
10 lis 00:59
Arnhus: nie mialem, ale za rok bede mial i to przykre, bo jade troche innym programem
10 lis 01:00
Arnhus: albo za 2 lata w sumie
10 lis 01:00
Arnhus: nie ogarniam matmy na razie
10 lis 01:00
Arnhus: dobra chyba rozumiem dzieki za pomoc
10 lis 01:02
Arnhus: moze Cie rozsmiesze na noc, ale bede musial brac rozszerzona matme
10 lis 01:03
Arnhus: heh, juz wiem co mi nie grało, pomylilem czesc calkowita z mantysa <wstyd>
10 lis 01:06
Artur_z_miasta_Neptuna:
oj tam ... cecha a mantysa −−− przecież to (prawie) to samo

za rok ... czyli obecnie NIE WIESZ co to liczba zespolona i
√−1 to coś co dla Ciebie nie
istnieje i tego się trzymasz
10 lis 01:13
Piotr:
@Artur
czy jest cos czego nie umiesz z matematyki ?

10 lis 01:16
Arnhus: jak wyprowadza się pochodną, tzn. skąd wzięły się wzory na stronie
357?
może ktoś wyprowadzić pierwszy wzór?
10 lis 15:52
Arnhus: 359 pomylka strony
10 lis 15:55
Artur_z_miasta_Neptuna:
właśnie ze strony 357

na której na samej górze masz podane jak wyznacza się 'wzór pochodnej z definicji'
10 lis 16:04
Arnhus: eh... przypomnę się wieczorem

10 lis 16:04
Arnhus: a co to lim?
10 lis 16:05
Arnhus: lim
h→0?
10 lis 16:07
Arnhus: no i czemu pochodna ze stałej liczby jest 0?
10 lis 16:10
Mati_gg9225535: lim − limes − granica

10 lis 16:11
Arnhus: dużo się dowiedziałem

10 lis 16:14
Artur z miasta Neptuna:
Granic nie miales a masz pochodne? cuuudo.
Dlaczego ze stalej pochodna wynosi zero −−− interpretacja geometryczna pochodnej w punkcie.
Pochodna w punkcie = tg (a)
gdzie a to kat jaki tworzy styczna do f(x) (w punkcie badanym) z osia OX
funkcja stala jest rownolegla do osi ox wiec styczna w kazdym punkcie to bedzie wlasnie ta
funkcja stala ... Ktora jest rownolegla do osi ox wiec nigdy jej nie przetnie wiec kat
pomiedzy styczna a osia ox wynosi 0 . tg 0 = 0
10 lis 16:31
Arnhus: mam troche inny program dlatego
10 lis 22:22
Arnhus: chyba rozumiem, ale powiedz cos jeszcze o tych granicach, bo zaraz calki beda i ...
10 lis 22:27
10 lis 22:46
Arnhus: 2449] i nadal nie wiem, co z tego wynika, że granicą tam będzie −2
10 lis 23:10
Arnhus: dobra już skumałem
10 lis 23:12
Arnhus: ale nadal nie rozumiem tego, co Artur napisałeś 16:31 :<
10 lis 23:24
Justina: F(x)=sgn(−1/2x+1)
21 wrz 16:59
KlasaV-VIII:
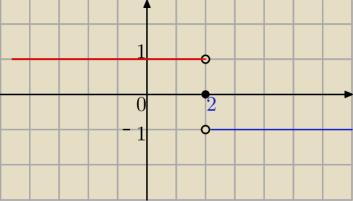
−1 dla x>2
0 dla x=2
1 dla x<2
21 wrz 17:32







 czy dla −[x] + 1 (czyli część całkowita
czy dla −[x] + 1 (czyli część całkowita )
w dziedzinie ważne jest myślenie ... 'dla jakiego 'x' to wyrażenie nie ma żadnego sensu
)
w dziedzinie ważne jest myślenie ... 'dla jakiego 'x' to wyrażenie nie ma żadnego sensu '
i tak.
np.:
'
i tak.
np.:


 jeżeli się mylę − to wybacz
jeżeli się mylę − to wybacz
 za rok ... czyli obecnie NIE WIESZ co to liczba zespolona i √−1 to coś co dla Ciebie nie
istnieje i tego się trzymasz
za rok ... czyli obecnie NIE WIESZ co to liczba zespolona i √−1 to coś co dla Ciebie nie
istnieje i tego się trzymasz

 na której na samej górze masz podane jak wyznacza się 'wzór pochodnej z definicji'
na której na samej górze masz podane jak wyznacza się 'wzór pochodnej z definicji'



 −1 dla x>2
0 dla x=2
1 dla x<2
−1 dla x>2
0 dla x=2
1 dla x<2