na trójkącie ABC opisano okrąg, oblicz współrzędne środka S tego okręgu oraz pro anna: na trójkącie ABC opisano okrąg, oblicz współrzędne środka S tego okręgu oraz promień R i pole P koła ograniczonego tym okręgiem,gdy A=(5,2). B=(3,0), C=(−3,6)

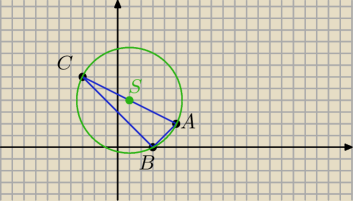
aniabb: S(1,4) R=2√5 P=πR² = 20π

Aga1.: Można np. tak Równanie okręgu o środku w S=(a,b) i promieniu r>0 (x−a)²+(y−b)²=r² , za x i y podstaw współrzędne punktów (5−a)²+(2−b)²=r² (3−a)²+b²=r² (−3−a)²+(6−b)²=r² Do pierwszego i trzeciego podstaw za r² r²=(3−a)²+b² i wykorzystaj wzory skróconego mnożenia 25−10a+a²+4−4b+b²=9−6a+a²+b² 9+6a+a²+36−12b+b²=9−6a+a²+b² a² i b² zredukujesz i otrzymasz układ równań z którego wyliczysz a i b. Sprawdź, czy nie ma pomyłki.

Aga1.: aniabb była sprytniejsza, bo zauważyła, że trójkąt ABC jest prostokątny (trzeba wykazać) .

Magda: a ja bym powiedziala ze jest to trojkat prostokatny a wiec srodek okregu opisanego na nim znajduje sie w polowie przeciwprostokątnej. wystarczy tylko znalezc srodek odcinka AC. a jak go znajdziemy mamy srodek okregu. do tego polowa przeciwprostokatnej jest promieniem, a gdy mamy promien mamy i pole

Aga1.: Magda masz rację, tylko mi nie chciało się sprawdzać, ani rysować i przedstawiłam ogólny sposób.

aniabb: zawsze powtarzam że podstawą geometrii analitycznej jest dobry rysunek a skoro teraz każda metoda jest dobra to odczytanie z rysunku powinno być uznawane

aniabb: trzeba poszukać co na to CKE bo dyskusja wrzała jakieś chyba 8−10 lat temu .. jak wprowadzali nową maturę

anna: aniubb wyniki się zgadzają ale jak to policzyć

aniabb: https://matematykaszkolna.pl/strona/1750.html

aniabb: https://matematykaszkolna.pl/strona/1248.html

aniabb: pierwszy link na środek okręgu , drugi na promień

anna: stokrotne dzięki spróbuje policzyć

aniabb: aby wykazać prostokątność trójkąta pr AB : y=x−3 pr BC : y=−x+3 1*(−1) = −1

krystek: Uważm ,ze na maturze należało wykazać ,że jest to Δ prostokątny (wystarczyło z rys policzyc dł boków) i wówczas zad jest zaliczone.

krystek: Lub tak jak aniabb poniewaz liczenie dł boków jest czasochłonne.

anna: niestety to nie wystarczy trzeba wszystko policzyć a mi nic nie wychodzi

krystek: To znajdź równania symetralnych dwóch boków i w ich przecięciu leży środek okręgu.

krystek: Następnie promień , to odległośc środka od wierzchołka trójkąta

krystek: Aga1 Tobie rozwiązała o 9,00

aniabb: krystek wstąpił do piekieł po drodze mu było

krystek: Ależ zgadzam się , ale sa osoby , które w klasie liczą tym sposobem i nie daja sobie rady z innymi .

aniabb: na starej maturze jak było 5h ma 3 zadania to wtedy trzeba było tak..teraz liczy się szybkość i zwięzłość

anna: coś robię żle bo nic mi nie wychodzi

Aga1.: Liczenie długości boków, czy znalezienie równań prostych też zajmuje trochę czasu. A znalezienie środka z zastosowaniem symetralnych to dopiero liczenia. Zauważ aniabb, że skrytykowałam się.

krystek: Jaki % uczniów w klasie ma taką sprawność?

aniabb: równanie prostej odczytujesz z rysunku znalazłam w CKE GEOMETRIA NA PŁASZCZYŹNIE KARTEZJAŃSKIEJ (GEOMETRIA ANALITYCZNA) Zdający posiada umiejętności w zakresie: wykorzystania i tworzenia informacji: interpretuje tekst matematyczny i formułuje uzyskane wyniki wykorzystania i interpretowania reprezentacji używa prostych, dobrze znanych obiektów matematycznych modelowania matematycznego: dobiera model matematyczny do prostej sytuacji użycia i tworzenia strategii: stosuje strategię, która jasno wynika z treści zadania rozumowania i argumentacji: prowadzi proste rozumowanie, składające się z niewielkiej liczby kroków.

aniabb: krystek.. a jakiej sprawności trzeba żeby liczyć kratki

aniabb: no i znać pitagorasa

Aga1.: anna, a który sposób wybrałaś?

krystek: 9:30 podałam.

aniabb: oo i ostatnie: prowadzi proste rozumowanie, składające się z niewielkiej liczby kroków.

aniabb: to po co 6 min później wymyślasz

krystek: Nie rozumiemy sie . Anna o 9:34 napisała ,że ona ma "liczyć ".

MQ: Moim zdaniem nie ma co liczyć na to, ze w każdym zadaniu tego typu znajdzie się jakiś sprytny sposób (a to trójkąt prostokątny, a to coś innego...). Trzeba uczyć się (nabierać sprawności) w rozwiązaniach ogólnych (jak podała Aga1), a sposoby to bonus.

Aga1.: krystek, jesteś kobietą?

krystek: tak !

anna: Aga1 liczylam i twoim sposobem i anibb i nic

Aga1.: Najpierw powinno się sprawdzić, czy zadanie uda się sprytnie rozwiązać.

aniabb: CKE dopuszcza : zdający potrafi .. znajdować stosunki miarowe w figurach płaskich i przestrzennych (także z wykorzystaniem układu współrzędnych lub trygonometrii),

Aga1.: To licz długości boków , linki masz podane. Zapisz swoje obliczenia.

Aga1.: I masz wnuka?

krystek: Tak.

MQ: Aga1:@9:55 Owszem, ale podawanie tylko "sprytnego" sposobu komuś, kto dopiero się uczy, nic mu nie daje, bo jak trafi na zadanie tego typu, gdzie "sposób" nie działa, to koniec. "Sprytny sposób" powinno się podać jako alternatywę −− i to z zastrzeżeniem, że tym razem tak działa i wytłumaczeniem, dlaczego.

krystek:

	xA+xC		xA+yC
@anna xs=		ys=
	2		2

krystek: @MQ i w pełni sie z Toba zgadzam !

aniabb: właśnie jak się uczy to trzeba pokazać jak to robić szybko i sprawnie, bo jak nie umie dookoła to liczy wprost..

aniabb: miałam przykład ostatnio kilku tumanów, którzy liczyli w pamięci skomplikowane przejścia z wykładniczej..bo tylko tak im pokazano..a potem banalne przekształcenia dalsze rozpisywali jak w 2 klasie podstawówki

anna: byłabym bardzo wdzięczna jakby mi ktoś to wyliczył i wytłumaczył

aniabb: aby wykazać prostokątność trójkąta pr AB : y=x−3 pr BC : y=−x+3 1*(−1) = −1 więc środek okręgu na środku boku AC

	xA+xC		yA+yC		5+(−3)		2+6
S(		;		) = (		;		) = (1,4)
	2		2		2		2

R− odległość od środka do A R²= (5−1)²+(2−4)² = 16+4=20 R=√20 = 2√5 P=πR2 = 20π

anna: dzięki bardzo

Eta: https://matematykaszkolna.pl/forum/164417.html Najprościej zmienić nick i czekać na gotowca

Ola: Cześć prześledziłam uważnie wszystkie wpisy w tym temacie i od kilku godzin staram się je zastosować do mojego zadania: w trójkącie o wierzchołkach A (5,8) B (−1,2) C (2,−1) oblicz pole i promień okręgu opisanego na nim i nie mogę sobie z tym nijak poradzić. Wychodzi mi a −40 i b 27 ale już r pierwiastek z 734 lub 782 zależy jak liczę. Czy możecie mi z tym pomóc?

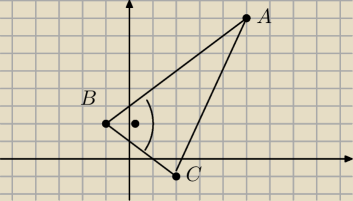
5-latek: jak dlugosc AC wyszla ?

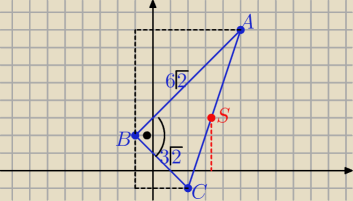
Eta: 1/ wyznaczam współczynniki kierunkowe prostych AB i BC

	yB−yA
aAB=		= ...= 1
	xB−xA

	yC−yB
aBC=		= ..= −1
	xC−xB

zatem proste AB i BC są prostopadłe więc ΔABC jest prostokątny 2/ |AB|=6√2 i |BC|=3√2 to P(ABC)= 0,5*3√2*6√2= 18 [j²] ======

	xA+xC		yA+yC		7		7
3/ S(		,		)= ..(		,		)
	2		2		2		2

4/ r²=(6√2)²+(3√2)² r²= 90 ⇒ r=3√10 =======

Eta: Poprawiam zapis 4/ c²=90 ⇒ c=3√10 to r=0,5c =1,5√10 ======

Ola: Bardzo dziękuję za pomoc. Tak szybko poradziliście sobie z tym zadaniem, że widzę jak wiele muszę jeszcze ćwiczyć. Teraz w takich zadanich będę od razu wykorzystywać wzory Ety. A zaraz zabieram się do moich obliczeń jeszcze raz, żeby sprawdzić czy potrafię dojść do tych samych wyników. Jeszcze raz dziękuję

Ola: Dobra zastosowałam wzory na długość boków |AB| i |BC| tzn. Pierwiastek z (xb−xa) 2 + (yb− ya) 2 i tak wyszło |AB|=6 pierwiastków z 2 i |BC|=3 pierwiastki z 2, a |AC|= pierwiastek z 58. Pole trójkąta to 1/2 a×h. Ale z jakiego wzoru Eto obliczyłeś promień i co to c?

Ola: A już wiem − c to przeciwprostokątna i do jej obliczenia posłużyło twierdzenie Pitagorasa, ale dalej nie wiem skąd wynik r?

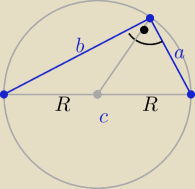
Eta: Podstawowa zależność

	1
c=2R ⇒ R=		c
	2

Eta: https://matematykaszkolna.pl/strona/541.html

5-latek: masz obliczyc pole okreo opisanego na tym trojkacie i promien tego okregu P= πr² r− polowa przecieprostokatnej c

	1
r=		c
	2

c−−−− to dlugosc odcinka AC A=(5,8) C= (2,−1) |AC|= √(2−5)²+(−1−8)²= √(−3)²+(−9)² = √9+81= √90 =c Nie ma potrzeby liczyc z PItagorasa skoro sie wie ze to trojkat prostokatny Wiadomosc ze to trojkat prostokatny jest potrzebna po to ze wtedy wiemy o tym ze promien okregu opisango na tym trojkacie tjest rowny polowie przeciwprostokatnej W tym trojkacie przeciwprostokatna to odcinek AC i nalezy policzyc jego dludosc (jest wzor na dlugosc odcinka |AC|=c= √90 = √9*10}= √9*√10= 3√10

	1
r=		c
	2

	3√10
r=		= po skroceniu 1,5√10
	2

Tyle

Eta:

5-latek: Dzien dobry Eta pozdrawiam

Eta: Witam Myślisz "małolatku" ,że nie potrafię wytłumaczyć Oli ....... Chciałam by sama włączyła myślenie i do tego doszła

5-latek: Oczywiscie ze potrafisz Tylko jak ja pisalem nie bylo Twoich wpisow na forum . Inaczej bym sie nawet nie odwazyl pisac

Ola: Aaa! Teraz mam już całkowitą jasność. Jesteście o niebo lepsi niż moi nauczyciele z lo przygotowujący mnie do matury. Jeszcze raz BARDZO dziękuję!

Eta:

5-latek: Twoi nauczyciele sa dobrzy Skad taki wniosek ?