Osobisty kącik samoudręczania.
Basiek: Osobisty kącik samoudręczania.
Może ktoś wrzuciłby mi jakichś 5 zadanek na dobranoc? Tylko nie takich, przy których mnie ranek
zastanie
Z góry dziękuję
27 gru 23:00
toja:
Podstawa? czy rozszerzenie?
27 gru 23:01
Basiek: Cóż, będę dzielna, poproszę rozszerzenie.
27 gru 23:01
ICSP: Ja tez mogę?
27 gru 23:02
Basiek: ICSP Twoje 1= 5 normalnych
Ale możesz, jak nie dziś, to jutro, pojutrze.... cóż, jest
czas, prawda?
27 gru 23:03
toja:
Hihi
......... pewnie,że możesz
27 gru 23:04
rumpek: Jaki dział
27 gru 23:09
Basiek: misz−masz
?
27 gru 23:09
ICSP: Udowodnij ze jednym z rozwiązań równania :
x
3 + 9x + 6 jest liczb x
1 =
3√3 −
3√9 xD
Jedno z moich ulubionych
27 gru 23:11
toja:
Zadania
tylko dla Basiek !
zad1/ Wykaż,że długość przekątnej pięciokąta foremnego o boku długości
a
zad2/ Wykaż,że dla a,b,c,d zachodzi nierówność
√(a+c)(b+d)≥
√ab+
√cd
zad3/ Wykaż,że: sin47
o+sin61
o−sin11
o−sin25
o= cos7
o
zad4/ Wyznacz zbiór wartości funkcji
a) f(x)=sin
2x*cos
4x+sin
4x*cos
2x
powodzenia ........... nie są trudne
27 gru 23:16
Basiek: Dziękuję
ICSP, dziękuję
Toja, postaram się zrobić
27 gru 23:17
hummel: Pokazac, ze zaden z ponizszych ciagów nie jest zbiezny
27 gru 23:20
Basiek: Hummel obawiam się, że badanie przebiegu ciągów wykracza poza moje kompetencje
27 gru 23:23
Basiek: ICSP Mógłbyś mi pomóc?
Mam 2 problemy, otóż:
dochodzę do postaci
| | 4 | | 8 | | 7 | | 11 | |
−3*3 { |
| } + 3 { |
| } + 3 { |
| } − 3 { |
| } |
| | 3 | | 3 | | 3 | | 3 | |
to {cds} są potęgi.
Więc
a) pomnożyć
−3 *3 do cośtam, czy to będzie 3
1 * 3 docośtam (wykładniki dodajemy) a na
koniec przed całość minus?
b) Cóż można z tym zrobić? Chyba pierwszy raz widzę taki przykład na oczy...
Na koniec− czy ja w ogóle idę dobrą drogą, czy powinnam coś rozkładać, etc?
27 gru 23:35
ICSP: Jeżeli potrafisz obliczyć ten pierwiastek to możesz go liczyć
wzory które mogą się przydać :
(a−b)
3 = a
3 − 3a
2b + 3ab
2 + b
3
i ogólnie o tyle. Wystarczy podstawić i policzyć. Przyznaję ze nie wyjdą ładne liczby ale
jakieś wyjdą.
27 gru 23:40
Basiek: No to przecież zastosowałam, doszłam do jakichś pierwiastków, potęg, bla bla, więc chciałam coś
z tym zrobić, to sobie wszystkie przestawiłam za pomocą 3−jki, bo się da. Pytam, co dalej
27 gru 23:42
ICSP: a gdybyś nie sprowadzała do potęg?
Na pewno ładniej by to było widać na pierwiastkach.
27 gru 23:46
Basiek: −33√81 + 33√243 + 93√3−93√9
27 gru 23:48
ICSP: zauważ że 81 = 27 * 3
oraz że 243 = 27 * 9
27 gru 23:49
Basiek: −9
3√3+9
3√9+9
3√3−9
3√9=
0 Dziękuję, już jaśniej.
27 gru 23:55
ICSP: Piękne udowodnienie xD
27 gru 23:55
ICSP: x
3 + 9x + 6 = 0
Δ = 36
√Δ = 6
x
1 =
3√−3 +6 +
3√−3−6 =
3√3 −
3√9
to inny sposób udowodnienia xD Jednak twoje chyba fajniejsze
27 gru 23:56
Basiek: Powinieneś dostać dyplom dręczyciela roku.
Nie miałam prawa tego zrobić w ten sposób i dobrze o tym wiesz.
27 gru 23:57
ICSP: Staram się jak mogę. Do końca roku już niedługo. Ciekawe ile głosów dostanę
28 gru 00:03
rumpek: sama prosiłaś
więc czego nazywasz
ICSP dręczycielem
28 gru 00:03
Godzio:
Zad 1/ od
toja pamiętam jak ja je dostałem, ehhh
28 gru 00:04
Pepsi2092: Siemano Wam wszystkim
Spora aktywność, tylko
ZKS brakuje
I Mistrzu
ICSP śpiący
już chyba bo tutaj minusa zgubił przy pisaniu wzoru na różnicę sześcianów ale i tak pozwólcie
że sobie zapiszę Wasze przykłady i zrobie dla siebie
28 gru 00:04
Basiek: Mój głos masz pewny... Ale to nic, i tak dzięki
Cóż, w międzyczasie Twojego zadania zrobiłam sobie
2gie− do potęgi, do potęgi... założenia a,b,c,d≥0
Końcowa postać a
2d
2+c
2d
2≥0
cnu.
i 4te:
a) ZW=<0,2>
b) ZW=<0,3>
Nad resztą... myślę !
28 gru 00:05
Basiek: Godzio − ja wiem, że sama chciałam, ale... ech, no przecież widzisz, że dla niego to jak
komplement
A
ZKS cały dzień pewnie nad rysunkami ślęczał
Niech się wyśpi chociaż
28 gru 00:07
Godzio:
Wracaj do 2
To nie jest końcowa postać
28 gru 00:07
rumpek:
4 a) inny wynik mam
b) jeszcze nie skończyłem
28 gru 00:07
Godzio:
4. a) popraw
b) popraw
28 gru 00:09
Godzio:
Skup się i nie spiesz
28 gru 00:09
Basiek: Cudownie, 3 dręczycieli... wow
28 gru 00:10
ICSP: Mam rywali
28 gru 00:12
Basiek: ICSP Skup się, bo ja mam tylko jeden głos
!
Tymczasem poprawione zad. 2gie:
(
√ad− p[cd])
2 ≥0
Lepiej?
PS. Klawiatura mi ześwirowała i odmawia zrobienia tej klamerki przy cd
28 gru 00:15
rumpek: ja w drugim otrzymałem:
(ad − bc)
2 ≥ 0
stosowny komentarz i gitara, natomiast u Ciebie b nie widze
28 gru 00:16
Basiek: ech
szczerze, to za każdym razem wbijam d zamiast b, mam "cb" tam.
Teraz będzie?
28 gru 00:18
Pepsi2092: 4a zbiór wartości ZW= <0;1> czy zwaliłem coś ?
28 gru 00:18
Godzio: Powinno być tak jak napisał
rumpek
28 gru 00:19
Godzio: źle
28 gru 00:19
rumpek:
zbiór wartości w 4a mam
ale więcej odpowiedzi nie podaje
bo tak jak napisała
Eta tylko dla
Basiek
28 gru 00:20
Pepsi2092: Oka dzieki dzieki
28 gru 00:22
Basiek: Co do ZW, możesz mi
Rumpek rozpisać, jak to zrobiłeś?
Ja chciałam łopatologicznie, ale okazuje się, ze chyba nie tędy droga. Trzeba to zamieniać na
funkcję jednej zmiennej, czy co?
28 gru 00:22
rumpek: ok, robię a) a potem spać
28 gru 00:23
Godzio: Mi się nudzi
Wyłączasz sin
2xcos
2x,
| | 1 | | 1 | |
sin2xcos2x(sin2x + cos2x) = sin2xcos2x = |
| * (2sinxcosx)2 = |
| sin2(2x) |
| | 4 | | 4 | |
28 gru 00:24
28 gru 00:25
Pepsi2092: Dobra wiem gdzie dałem ciała doszedłem do postaci −cos
4+cos
x izamiast wprowadzic zmienna
pomocnicza t i liczyć współrzędne to ja jako zbiór wartości napisałem warunek jaki t powinno
spełniac
ale dzięki
28 gru 00:25
Pepsi2092: −cos
4+cos
2x
28 gru 00:25
kylo1303: W zadaniu drugim aby na pewno nie powinny być tam pierwiastki? Tj:
(√ad−√bc)2≥0
zad 4a mam tak samo jak rumpek, ale w 4b tak jak napisał/a Basiek czyli <0,3> i to jest
źle?
28 gru 00:26
Adicted: Jestem uzależniony pomożecie mi ?
28 gru 00:27
Godzio:
Jest ok <0,3>, źle oczytałem przykład
28 gru 00:27
rumpek: a) f(x)=sin
2x*cos
4x+sin
4x*cos
2x
sin
2xcos
2x(cos
2x + sin
2x)
sin
2xcos
2x*1 = sin
2xcos
2x = (sinxcosx)
2
i teraz korzystam ze wzoru 2sinx = 2sinxcosx
| | 1 | | 1 | |
( |
| *2sincosx)2 = ( |
| sin2x)2 |
| | 2 | | 2 | |
| | 1 | | 1 | | 1 | |
no to teraz już chyba wiadomo sin2x ⇒ <−1;1>; |
| sin2x ⇔ <− |
| ; |
| > |
| | 2 | | 2 | | 2 | |
no i teraz tylko do kwadratu pamiętając, że jak kwadrat to od zera zaczynamy
| | 1 | |
i mamy <0; |
| > |
| | 4 | |
28 gru 00:28
Basiek: [TU CENZURA]
Jej, pierwszy raz coś takiego widzę. Ja bym to wszystko łopatologicznie, jak np. cosx∊<−1,1> ,
cos2∊<0,1> itd...
Cóż, przynajmniej się czegoś nowego nauczyłam. Chyba ktoś coś przeoczył w mojej edukacji...
28 gru 00:28
ICSP: DOŚĆ
Wszyscy zostawić zadania
Basiek jak komuś się nudzi to dam mu zadanie
28 gru 00:29
rumpek:
28 gru 00:30
Godzio:
Daj
28 gru 00:30
rumpek: Jaka stanowczość
28 gru 00:30
Pepsi2092: Daj mi Mistrzu jakies z trygonometrii tylko napisz mi czy w tym przykładzie b trzeba korzystać
ze wzoru na cos2α bo tak na pierwszy rzut oka mi się coś wydaje, ale dobra to zadania
Basiek
28 gru 00:31
Basiek: Okej, to przykład
ZW=<0,3> ?
28 gru 00:32
ICSP: | | x−9 | | π | |
1.W jakim punkcie styczna do krzywej y = |
| tworzy z osią OX kąt α = |
| ? |
| | x+7 | | 4 | |
2.Liczby x
1 i x
2 są pierwiastkami równania : x
2 − 3x + A = 0 a liczby x
3 i x
4 to
pierwiastki równania x
2 − 12x + B = 0 . Wiadomo że liczby x
1,x−2,x
3,x
4 tworzą ciąg
geometryczny. Znajdź A i B
28 gru 00:34
ICSP: tam powinno być x2
28 gru 00:35
Adicted: | | a+b | | a−b | |
wykaż że sina + sinb = 2sin |
| + cos |
| |
| | 2 | | 2 | |
28 gru 00:35
Basiek: Adicted− a to komu?
28 gru 00:36
Pepsi2092: Dzięki już włączam myślenie
28 gru 00:36
Adicted: Panu Panie Basiek
28 gru 00:37
ICSP: nie + tylko *
28 gru 00:37
ICSP: Adicted to jest ona
28 gru 00:38
Adicted: no faktycznie
28 gru 00:38
Adicted: skad wiesz ?
28 gru 00:38
Basiek: Pani, Pani Basiek *
Trzeba być okropnie domyślnym, żeby zorientować się, że na imię mam Barbara, Baśka, Basia etc.,
i że jestem kobietą?
− nie sądzę.
28 gru 00:38
Adicted: powiem wiecej trzeba byc okrutnie domyślnym
28 gru 00:40
Basiek: Przykro mi, że nie wszyscy są "okrutnie domyślni"
Ale to nic, dzięki za zadanko
28 gru 00:42
Adicted: ICSP = Institute of Corporate Secretaries of Pakistan, w dobrą stronę ide ?
28 gru 00:42
ICSP: nie xD
28 gru 00:43
Godzio:
Tak na szybko:
1.
x = −3 lub x = − 11
Zad. 2
A = 2 i B = 24
lub
A = − 18, B = −72
28 gru 00:44
Basiek: In−Circuit Serial Programming ?
28 gru 00:44
28 gru 00:45
Adicted: Żongluje ktoś z was może ? Podobno to wpływa pozytywnie na pracę mózgu
28 gru 00:46
ICSP: przykro mi Godziu ale obydwa źle.
W pierwszym chyba nie znasz definicji punktu
W drugim B jest źle.
28 gru 00:47
ICSP: Nadal nie trafione. W zupełnie inną stronę powinieneś iść
28 gru 00:47
Godzio:
Dobra to na kartce robię, myślałem że raz spróbuję w pamięci zrobić, ale nie wyszło, jeszcze
nie ten moment
28 gru 00:48
kylo1303: Ja żongluje, standardowo 3 pileczkami. To ma niby synchronizowac polkule mozgowe, przez co
praca mozgu mialaby byc bardziej wydajna. Osobiscie sadze ze w praktyce wiekszego zastosowania
to nie ma, ale mozna sie za to odstresowac.
28 gru 00:48
Godzio:
Ale styczne mogą być dwie
więc i punkty też dwa
28 gru 00:49
Basiek: Okej, a teraz ktoś będzie tak
miły i kochany i powie mi, co robię znów źle.
Zadanie drugie
√(a+c)(b+d)≥
√ab+
√cd /
2
ab+ad+cb+cd≥ ab+cd+ 2
√abcd
ad+cb−2
√abcd≥0
(
√ad−
√cb)
2≥0
Dziękuję
28 gru 00:49
Adicted: na pewno nigdzie nie ma błędu ?
28 gru 00:49
Adicted: Godzio weź nie demotywuj dobra ?
28 gru 00:50
Godzio:
Tak też może być
28 gru 00:50
Adicted: Fajne zdanie ,,przez co praca mozgu mialaby byc bardziej wydajna. Osobiscie sadze ze w praktyce
wiekszego zastosowania to nie ma''
28 gru 00:52
ICSP: Godziu
PUNKT MA DWIE WSPÓŁRZĘDNE
28 gru 00:52
Pepsi2092: tgα= a czyli a=1 i ta styczna ma postać y=x+b, ale chyba coś źle myślę
ale to b jak
wyznaczyłeś ?
bo potem to chyba układ bedzie ?
Ale coś mam za duzo niewiadomych
28 gru 00:52
Basiek: Ja tu oszaleję Wątek jest SPERSONALIZOWANY.
Wskazuje na to słowo "osobisty" "samo−udręczenia"
O ile ICSP, toja, Godzio, Rumpek, a nawet Pepsi mi nie przeszkadzają, to Adicted
działasz mi na nerwy, zajmij się matematyką lub czymś pokrewnym, albo idź do innego wątku.
<wredna Baśka>
28 gru 00:52
rumpek:
(a + c)(b + d) ≥ ab + cd + 2√abcd
ab + ad + bc +cd − ab − cd ≥ 2√abcd
ad + bc ≥ 2√abcd / ()2
(ad + bc)2 ≥ 4abcd
(ad)2 + 2abcd + (bc)2 ≥ 4abcd
(ad)2 − 2abcd + (bc)2 ≥ 0
...
28 gru 00:53
Adicted: trzeba specjalną emotke stworzyć
dobra masz racje nie przeszkadzam
28 gru 00:53
Godzio:
W pierwszym jestem pewien, że nie ma błędu
28 gru 00:53
Godzio:
Aaaa
(−3,−3) i (−11,5)
28 gru 00:54
Basiek: No ok. Łapię, ja tego znów nie spotęgowałam, mimo wszystko... wydaje się, że ten wzór tam
pasuje... więc, nie rozumiem−co jest źle?
28 gru 00:55
Godzio:
Jest dobrze Baśka !
28 gru 00:56
Basiek: Noo, wreszcie.
Dzięki
Godzio słowa Twe, jak balsam dla mojej duszy.
28 gru 00:56
ICSP: Teraz pierwsze dobrze
28 gru 00:57
Pepsi2092: Za bardzo Cię lubimy
Basiek
28 gru 00:58
kylo1303: Co do zadanie 2 ICSP to wyniki:
A=2 B=32 lub A=−18 B=−288 ?
28 gru 00:58
Godzio:
W 2 niech się inni męczą, zrobiłem jakiś błąd rachunkowy, nie chce mi się robić tego ponownie
28 gru 00:58
Basiek: Pepsi nie słodź, nie słodź.
Napoje tego typu właśnie przez to, że takie słodkie, tak
bardzo szkodliwe
I wiecie co?
Chyba znikam− po wczoraj mam bana na siedzenie po nocach
28 gru 00:59
Godzio:
Uuuu było lanie
28 gru 01:00
ICSP: Tak kylo1303 to są poprawne wyniki.
Teraz takie łapcie : Pole powierzchni wielościanu opisanego na kuli wynosi 9cm2 a jego
objętość to 12cm3. Oblicz promień kuli.
28 gru 01:01
Pepsi2092: haha
Chciałem trochę poprawić atmosferę, a poza tym wiesz
Adicted też chce się trochę
odchamić i mieć kontakt z ludźmi
28 gru 01:01
kylo1303: tego z kula nie bede robil bo nie czuje sie najmocniej w tego typu zdaniach, jak ktos napisze
to przesledze. Mam jeszcze pytanie odnosnie zadania:
√(a+c)(b+d)≥√ab+√cd
Czy tutaj sa jakies zastrzezenia? Bo jesli nie to zadanie jest bledne (albo ja zle mysle xD)
28 gru 01:05
Godzio: Czemu błędne
? (założenie jest a,b,c,d≥0)
28 gru 01:06
Basiek: Godzio masz bujną wyobraźnię
Nigdy mnie o tak nieludzkiej porze jak 4rta przed
komputerem nie nakryto, gdyż, bowiem, ponieważ... chowam laptopa pod kołdrę <esz,
oryginalność>
@ Pepsi, jasne, zapraszam, tylko wiesz, to był taki offtop jak rzadko
Ja zazwyczaj udaję, ze
trzymam się tematu. A wybacz− żonglowanie, jakieś nowe metody nauki i inne takie... bądźmy
szczerzy− wszystkie te posty zignorowano−
Ty również.
28 gru 01:06
Godzio:
Baśka siedzi o 4 rano przed kompem, wchodzi mama:
Mama: Co Ty do jasnej cholery robisz ?
Baśka: Yyyy robię zadania z matmy
Mama: Masz bana !
28 gru 01:07
ICSP: Godziu masz bana mnie rozwaliło. Szkoda że nie ma przycisku lubię to
28 gru 01:08
kylo1303: Godzio Przy tym zalozeniu jest ok, po prostu w tresci zdania byl blad, tj nie dopisane
"≥0" wiec chcialem sie upewnic.
28 gru 01:08
Godzio:
toja nie dopisała
28 gru 01:09
Basiek: Za dużo fejsbuuka,
ICSP
Swoją drogą, też się pośmiałam
A zadania mogę robić ile chcę, tylko jak faktycznie chodzę do
szkoły... cóż, dziwne, jak tak na to spojrzę
Chyba jak ktoś mówi, gdy ma wolne "robię zad."
jest niewiarygodny.
28 gru 01:10
Godzio:
E tam jak miałem szkołę to i tak siedziałem długo, rano wstawałem: patrze, 7:30 i myślę hmmm,
teraz jest polski, a tam nie idę i dalej w kime
28 gru 01:12
kylo1303: ICSP Jakas podpowiedz do zadania z kulą, bo jednak sprobuje swoich sil? Tylko ze narazie
zatrzymalem sie na tresci.
28 gru 01:13
kylo1303: Godzio Haha, jakbys czytal mi w myslach xD
28 gru 01:13
Basiek: Godzio ja najczęściej chodzę o 2giej, wstaję punk 5:45. W pierwszej klasie (nadrabiałam
zaległości z gimnazjum)− chodziłam spać o 3ciej/ 4tej. Więc no, też krótko nie siedzę.
RAZ nie poszłam na pierwszy polski, bo kobita nie sprawdza obecności. Niestety na ten genialny
plan wpadła połowa klasy, więc raz nie poszłam= nieobecność.
Już się tak nie bawię
28 gru 01:15
Godzio:
E tam, ja sobie usprawiedliwienia pisałem
28 gru 01:16
Basiek: Że jakie usprawiedliwienia− nie przyszedł, bo zaspał?
28 gru 01:18
ZKS:
A gdzie zadania zrobione?
Najpierw robimy później rozmawiamy na różne tematy.
28 gru 01:18
Godzio:
No właśnie ja tak miałem fajnie, że "Proszę usprawiedliwić nieobceność syna dnia blabla"
koniec
28 gru 01:19
ICSP: | | 1 | |
Vwieościanu = |
| * Pwielościanu * R |
| | 3 | |
jest taki wzór.
28 gru 01:19
kylo1303: "Teraz takie łapcie : Pole powierzchni wielościanu opisanego na kuli wynosi 9cm2 a jego
objętość to 12cm3. Oblicz promień kuli."
R=4
28 gru 01:20
kylo1303: Przy czym dodam ICSP ze dalem rade bez tego ostatniego postu, sam sobie wyprowadzilem
zaleznosc xD
28 gru 01:20
Godzio:
ICSP weź go wyprowadź bo ciekawy jest
28 gru 01:21
Basiek: Godzio ja tak nie mam
Za to u mnie w szkole można nie chodzić na języki, bo są osobne
dzienniki, a nikomu nie chce się przepisywać obecności
ZKS − czeeeść, jak rysunki?
28 gru 01:21
ICSP: żebym to ja jeszcze wiedział jak go wyprowadzić...
28 gru 01:22
kylo1303: Objetosc wieloscianu opisanego na kuli to suma objetosci ostroslupow o wysokosci R i podstawie
rownej polu jednej sciany.
Pś −pole sciany
Pc− pole calkowite
n− ilosc scian
R− promien
Pc=n*Pś
28 gru 01:23
ZKS:
Cześć
Basiek! Zrobiłem 1 serię z kreski i trochę zacząłem rzut parteru więc powoli ale
jakoś idzie.
A Tobie jak tam idą zadania które podała
toja?
28 gru 01:25
Basiek: ŹLE
Właśnie szukam wzoru na różnicę sinusów, bo chyba nie znam
28 gru 01:26
kylo1303: | | α+β | | α−β | |
sinα−sinβ=2*cos |
| *sin |
| |
| | 2 | | 2 | |
28 gru 01:28
Basiek: Już sobie znalazłam, ale i tak dzięki,
kylo
28 gru 01:29
kylo1303: ICSP Mógłbyś dac jakeis jeszcze zadanko (poziom liceum−rozszerzony)? Bo nie chce ruszac
tych od
toja zeby nie bylo
28 gru 01:30
28 gru 01:31
ICSP: Dla jakich wartości parametru α najmniejsza wartość funkcji :
f(x) = x2 − 2x + cos2α + sinα + 3 jest równa 3 ?
28 gru 01:32
28 gru 01:32
Godzio: ZKS
ICSP
Ja
Basiek
kylo
Dla nas są jabłka
Dobrze, że reszta poszła bo by nie starczyło
28 gru 01:36
ZKS:
ICSP jeśli się nie pomyliłem to wyszło mi że dla
| | π | | 5 | | π | | 3 | |
0 , |
| , |
| π , |
| , |
| π? |
| | 6 | | 6 | | 2 | | 2 | |
28 gru 01:36
ICSP: zgubiłeś okresowość ale wyniki
28 gru 01:37
ZKS:
Słuszna uwaga
Godzio.
Jedno nawet jest z po kropce jabłko.
28 gru 01:37
toja:
To robaczywe z kropką jest dla
ICSP
Dobranoc
28 gru 01:39
ZKS:
Okej dzięki.
Właśnie nie wpisałem okresu bo sam sobie wziąłem przedział <0 , 2π).
28 gru 01:39
Godzio:
Dobranoc
28 gru 01:40
ZKS:
Basiek gdzie znikłaś?
28 gru 01:41
ICSP: Wiedziałem że to jest dla mnie xD
28 gru 01:42
Godzio:
Neta odłączyli
28 gru 01:42
ZKS:
Jak się siedzi do rana na komputerze to i odłączają.
28 gru 01:45
Basiek: Ych, ja − myślę. Nad moim 3cim zadankiem.
Jak krew z nosa idzie, dosłownie.
28 gru 01:46
ZKS:
Kiedyś nawet robiłem to 3 zadanie pamiętam.
28 gru 01:46
Basiek: Wierzę, też będę je dłuuugo pamiętać.
28 gru 01:47
ZKS:
Powiem szczerze bardzo ciekawe jest to zadanie mogę dać wskazówkę jak coś.
28 gru 01:50
Godzio: Ja już lecę, dobranoc i powodzenia z zadaniami
28 gru 01:52
Basiek: L= 4sin18*cos36*cos7
P=cos7
Tu utknęłam na dobre i żadne forum/ wzory/ cokolwiek nie pomaga mi wpaść, jak dalej.
28 gru 01:53
kylo1303: "Dla jakich wartości parametru α najmniejsza wartość funkcji :
f(x) = x
2 − 2x + cos2α + sinα + 3 jest równa 3 ?"
Gdzie popelniam blad?
f(1)= 1 − 2 + cos2α + sinα + 3=3
cos2α + sinα − 1= 0
1 − 2sin
2α+sinα −1 =0
2sin
2α−sinα=0
Bo wyniki nie beda takie jak u
ZKS
28 gru 01:53
Basiek: Godzio 
28 gru 01:53
ZKS:
Dobranoc
Godzio.
28 gru 01:53
ZKS:
Jak to nie będą takie same?
28 gru 01:54
kylo1303: Basiek A co tego 3ciego zadania to zatrzymalem sie podobnie jak ty, a jak probowalem dalej
"po swojemu" to w ogole wyszlo ze nie moze byc cos takiego xD
28 gru 01:55
ZKS:
Basiek napisz wszystko jak rozwiązujesz wtedy się zobaczy czy czegoś po drodze nie gubisz.
28 gru 01:55
kylo1303: z pierwszego bedzie "kπ" (dla k∊C), z drugiego bede mial 2 serie. U ciebie jest natomiast 5
wynikow (pomijam okresowosc).
28 gru 01:56
Basiek: Nie, nie gubię... wzorkami wszystko robię. Poza tym
Kylo ma tak samo!
Przepisywanie
tego zajmi mi wieeeczność.
28 gru 01:57
Pepsi2092: ZKS dowodzik jakiś poproszę jesli mozesz coś wrzucić na poczekaniu
z góry dzieki
wielkie
28 gru 01:58
kylo1303: Ja sie zatrzymalem na takim:
| | 1 | |
L= 2cos7o* (cos36o−2cos236o+1) czyli z tego by wynikalo ze (cos36o−2cos236o+1)= |
| , |
| | 2 | |
pociagnac to dalej to nie wyjdzie, ale moze machnalem sie gdzies w obliczeniach.
28 gru 01:58
ZKS:
| | π | | 3 | |
Bo ja źle napisałem nie będzie |
| i |
| π bo wiadomo że jest to 1 pomyliłem się. |
| | 2 | | 2 | |
28 gru 01:58
ZKS:
Ja jakoś tutaj to zadanie zrobiłem i wieczności mi nie zajęło
Basiek.
28 gru 01:59
kylo1303: Podejme sie napisania mojego toku rozumowania, moze jest gdzies blad.
28 gru 01:59
Basiek: Z mojego by wynikało, że 4sin18*cos36=1 , ale naprawdę nie wiem jak dalej stąd ruszyć
A jak
wbijam w kalkulator, to faktycznie 1 wychodzi z tych dwóch składników
28 gru 02:00
ICSP: kylo1303 może być dowodzik z planimetrii?
28 gru 02:01
Basiek: <3 To może o tych dwóch kołach i udowodnij, że trapez?
28 gru 02:02
ICSP: | | 4 * sin180 * cos18 * sin36 | | sin72 | | cos18 | |
4 * sin18 * sin36 = |
| = |
| = |
| = |
| | cos18 | | cos18 | | cos18 | |
1
28 gru 02:02
ICSP: To przecież jest proste xD
28 gru 02:02
ZKS:
| | 2 | | n | | m | | m | |
A = |
| + ( |
| + 2 + |
| ) * |
| |
| | n − m | | m | | n | | m2 − n2 | |
Uzasadnij że odwrotność liczby A jest liczbą naturalną.
n ≠ m oraz n , m ∊ ℕ.
Proszę
Pepsi2092.
28 gru 02:03
kylo1303: | | 108 | | 14 | | 36 | | 14 | |
sin47 + sin61 − (sin11 + sin25)= 2*sin |
| *cos |
| − 2*sin |
| *cos |
| =
|
| | 2 | | 2 | | 2 | | 2 | |
=2cos7*
(sin54−sin18)= 2cos7* [sin(90−36) − sin(90−72)]= 2cos7 * (cos36−cos72)= 2cos7 *
[cos36− (2cos
236−1)]= 2cos7 (−2cos
236+cos36+1)=−2cos7(2cos
236−cos36−1)
Tam gdzie podkreslone mozna tez uzyc na roznice sinusow ale to chyba mi nie wyszlo.
28 gru 02:04
Pepsi2092: dziękować dziękować, juz myślę
28 gru 02:05
ZKS:
Gubicie cos7
o i dlatego wam tylko 1 wychodzi.
28 gru 02:05
Basiek: Ależ wyszło
Bez paniki.
ICSP dzięęęki. I nie używaj słowa "proste".
28 gru 02:06
ICSP: to przecież jest skomplikowane
28 gru 02:08
kylo1303: "kylo1303 może być dowodzik z planimetrii?" Mozesz dac, aczkolwiek o zadanie pytal
Pepsi2092, ja bede probowal robic co dacie.
28 gru 02:08
kylo1303: ICSP wypowiedz z 2:02 :
co tam robi sin180?
28 gru 02:10
ICSP: wredne 0
28 gru 02:12
kylo1303: Dobra, juz wiem. Mialo byc sin18
28 gru 02:12
Basiek: ICSP − lepiej
Szybko się uczysz.
To ja też wrzucę, poziom LO (nie wiem, czy proste, czy trudne− nie robiłam)
Wykaż, że jeżeli długości a,b,c trójkąta spełniają warunek a
2=b
2+bc, to w tym trójkącie miara
kąta wewnętrznego leżącego naprzeciwko boku dł. a, jest dwa razy większa od miary kąta
wewnętrznego leżącego naprzeciwko boku dł. b.
28 gru 02:12
ICSP: Na czworokącie ABCD można opisać okrąg. Niech P,Q,R,S będę rzutami prostokątnymi punktu
przecięcia przekątnych czworokąta. na proste zawierające kolejne boki. Udowodnij że w
czworokąt PQRS można wpisać okrąg.
28 gru 02:13
ZKS:
Ach mój ulubiony rozdział.
28 gru 02:15
kylo1303: ZKS Zadanie z 2:03
| | 1 | | 1 | |
Po wykonaniu dzialan wychodzi A= |
| wiec |
| =n |
| | n | | A | |
28 gru 02:15
Basiek: ZKS jak chcesz, mam na pewno jeszcze coś 'super' z prawdopodobieństwa
28 gru 02:17
ZKS:
Ty
Basiek bo za chwilę dam takie zadnie że tylko
ICSP będzie wstanie to rozwiązać.
28 gru 02:19
Basiek: Ja się już chyba niczym nie przejmę
A to zadanko z prawdopodobieństwa to sama chciałabym
wiedzieć, jak rozwiązać
Ale cóż
Nie, to nie, ja nikogo zmuszać nie będę
28 gru 02:21
kylo1303: do zadania ICSP potrzebuje dobrego rysunku a nie chce mi sie ruszac z lozka, obliczenia
moge robic "na kolanie" ale z planimetria tak latwo juz nie pojdzie.
28 gru 02:22
kylo1303: Basiek to daj z prawdopodobienstwa, z checia zrobie (albo i nie)
28 gru 02:22
ZKS:
Hehe żartuję wrzucaj zadanie ktoś na pewno będzie wstanie Ci pomóc.
28 gru 02:22
Basiek:
Do sklepu dostarczają żarówki dwa zakłady, będące częściami tej samej firmy, przy czym
pierwszy z nich dostarcza trzy razy więcej żarówek niż drugi. W pierwszym z nich średnio 3
żarówki na 1000 wyprodukowanych, a w drugim 7 na 1000 ma wady.
Klient kupił żarówkę, na która .. bla bla blaaaa... Żarówka ta w okresie gwarancji zepsuła się.
Do którego zakładu sklep powinien raczej się zwrócić z reklamacją?
Dział: prawdopodobieństwo całkowite, stopień trudności : ** (zadania typu− nie ruszaj)
28 gru 02:27
Pepsi2092: Zeby nie było że tak długo robię ale postaram się to przepisac i mi powiecie gdzie błąd robię
28 gru 02:27
kylo1303: Basiek Zadanie z 2:12
Wiesz moze czy to robic z twierdzenia cosinusow? Bo doszedlem do czegos takiego i nie wiem czy
ciagnac dalej (moja teza to α=2β):
Nie skorzystalem jeszcze z tego:
c
2=a
2+b
2+2abcos(α+β)
Moglbym dalej cos probowac ale nie wiem czy to ma sens.
28 gru 02:33
Basiek: Chyba nie bardzo
SPOILER
Podpowiedź: Na przedłużeniu boku AC odłóż odc. AD= c, tu korzystasz z a
2=b
2+bc. jak sobie
ładnie podzielisz stronami przez ab, no i korzystasz z podobieństwa Δ .
28 gru 02:36
kylo1303: Twoje zdanei z prawdopodobienstwa mozna rozwiazac na 2 sposoby, jeden to korzystac ze wzorow na
Praw. calkowite itp, drugi jest duzo prostszy ale "omija" dzial.
I zaklad produkuje 3x zarowek, praw. ze bedzie zepsuta to 3/1000
II zaklad produkuje x zarowek , 7/1000
Czyli:
| | 9x | |
Z zakladu pierwszego do sklepu idzie |
| zlych zarowek
|
| | 1000 | |
| | 7x | |
Z zakladu drugiego do sklepu idzie |
| zlych zarowek
|
| | 1000 | |
Widac ze wiecej zlych produkuje zaklad I
28 gru 02:37
kylo1303: Basiek aha, problem w tym ze jak juz napisalem nie wykonuje rysunkow (albo tylko takie
smieciowe do ogolnej pomocy), dlatego nie bardzo mialem mozliwosc cokolwiek zauwazyc
28 gru 02:38
Pepsi2092: Zrobiłem
przepisze to mi spr
28 gru 02:40
Basiek: Kylo to sobie odpuść planimetrię i stereometrię, bo bez rysunków to się chyba nie da.
Co do zad. powyżej, dzięki, jesteśmy co prawda kilka stron "przed" i pewnie i tak będę musiała
wykorzystać wzory, aleee okazuje się, że nie takie dwie gwiazdki trudne, jak je malują
28 gru 02:41
ZKS:
To ja może wrzucę jakieś zadanko ciekawe hmm?
28 gru 02:43
Basiek: O,a to?
Zadanie Banacha. Pewien matematyk ma dwa pudełka zapałek, w każdym po N zapałek. W momencie,
gdy potrzebuje zapałki, wybiera losowo pudełko, a z niego zapałkę. Musi nadejść taki moment, w
którym jedno z pudełek okaże się puste, jakie jest prawdopod. , że w drugim pudełku znajduje
się dokładnie K zapałek ?
28 gru 02:44
kylo1303: Wrzucaj. Tylko wlasnie jest jedno zastrzezenie, ze tak jak zrobilem to korzystamy co najwyzej z
definicji. Jesli ktos wymagalby zeby zadanie zrobic tak jak sie powinno z prawd. calkowitego
to bedzie wygladalo troche inaczej, mysle ze moge napisac jak jesli chcesz (i jesli mi
wyjdzie)
28 gru 02:45
Basiek: Jeśli Ci się chce
Ja zawsze chętnie patrzę na mądre wywody matematyczne 8−)
28 gru 02:46
ZKS:
Basiek czyżby zbiór zadań z Oficyny Edukacyjnej Pazdro?
28 gru 02:47
Basiek: Taaaak!
28 gru 02:47
ZKS:
Fajny zbiór dużo ciekawych zadań sam w liceum miałem ten że zbiór.
28 gru 02:49
Basiek: Jestem całkiem innego zdania. Chociaż wiele pewnie zależy od nauczyciela. Ale rozwiązywanie
sobie tych zadań samemu na podstawie tej (strrasznej, głupiej, zuej...) książki jest torturą
28 gru 02:51
Pepsi2092: | | 2 | | n2+2nm+m2 | | m | |
A= |
| + |
| * |
|
|
| | n−m | | mn | | (m−n)(m+n) | |
| | 2 | | (n+m)2*m | |
A= |
| + |
|
|
| | n−m | | mn(m−n)(m+n) | |
| | 2(m−n)*n+(n+m)(n−m) | |
A= |
|
|
| | (n−m)(m−n)*n | |
| | 2mn−2n2+n2−m2 | | 2mn−n2−m2 | |
A= |
| = |
| | /−1
|
| | (n−m)(m−n)*n | | (n−m)(m−n)*n | |
Sorry że tak długo mi schodzi ale słabo sobie jeszcze radz z pisaniem tutaj
28 gru 02:52
ZKS:
Jeżeli ktoś zdaje na podstawie matematykę to lepiej niech korzysta z innego zbioru.
28 gru 02:53
ZKS:
Pepsi2092 gotowy na kolejne zadanie?
28 gru 02:55
Pepsi2092: ZKS a Ty z czego się przygotowywałeś do matury z jakich zbiorów ?
Bo ja korzystam z
dwóch części Kiełbasy, mam też też zbiór zadań z oficyny, 11 i 12 z operonu i jeszcze Aksjomat
i tam zbiór bodajże Alicji Cewe tylko jak możesz to doradx mi z czego najlepiej cisnąć bo i
tak przeciez nie dam rady zrobić 10 000 zadań do maja i ze wszystkich zbiorów
28 gru 02:56
Basiek: Moim zdaniem spora większość zad. jest powyżej poziomu maturalnego, a nauczycielka ma problem
je zrobić. Cóż− życie.
Na lekcji przerabiamy też inny zbiór, prostszy
Co do Pazdro− może
się kiedyś przekonam do niego. Po świętach w każdym razie kupuję zbiory Kiełbasy
28 gru 02:56
Pepsi2092: no dawaj dawaj Mistrzu
Tylko takie do godzinki czasu bo wiesz jutro mam normalne dodatkowe
lekcje w sql z matmy i angielskiego i o 7 pobudka ale jeszcze jedno wrzucaj jak masz
28 gru 02:57
kylo1303: (nie wiem czy za bardzo nie utrudnilem, ale tak na 2 gwiazki by pasowalo)
| | 3 | |
Z1 produkuje |
| calosci, 3/1000
|
| | 4 | |
P(A) − prawdopodobienstwo wylosowania wadliwej zarowki
| | 3 | | 9+7 | | 4 | |
P(A)=P(B1)*P(A/B1)+P(B2)*P(A/B2)= |
| *3/1000+1/4*7/1000= |
| = |
|
|
| | 4 | | 4000 | | 1000 | |
Naszym zadaniem jest sprawdzenie co jest wieksze: P(B
1/A) czy P(B
2/A).
| | P(B1∩A) | | P(A∩B1) | |
P(B1/A)= |
| = |
|
|
| | P(A) | | P(A) | |
| | P(A∩B1) | |
P(A/B1)= |
| → P(A∩B1)=P(A/B1)*P(B1) (podstawiam do pierwszego)
|
| | P(B1) | |
| P(A∩B1) | | P(A/B1)*P(B1) | |
| = |
| (tutaj juz wszystko jest znane)
|
| P(A) | | P(A) | |
Tak samo z drugim, potem porownac i powinno wyjsc.
28 gru 02:59
ZKS:
Pepsi2092 Aksjomat to jest naprawdę świetny zbiór zadań przygotuje Cię na co najmniej 80%
z rozszerzenia z matematyki (oczywiście jeżeli będziesz przerabiał sporo zadań z tego zbioru)
więc bardzo go polecam Alicji Cewe też jest dobry Pazdro arkusze maturalne również (te
ostatnie bym powiedział że nawet bardzo trudne).
28 gru 03:03
Basiek: Napisz mi jeszcze, proszę, co oznacza B
1 i B
2
28 gru 03:03
ZKS:
Ale najważniejsze to przychodzić tutaj na forum i rozwiązywać zadania podawane przez
forumowiczów bo tutaj masz różny poziom i różne dział więc to daje więcej niż nie jeden zbiór.
28 gru 03:06
ZKS:
Basiek kto szuka nie błądzi.
61160
28 gru 03:07
kylo1303: Uzylem B zamiast "Z"
P(B1)− prawd. ze wylosowana zarowka bedzie z zakladu 1
P(B2)− prawd. ze wylosowana zarowka bedzie z zakladu 2
P(A/B1)− prawd. ze wylosowana zarowka z zakladu 1 bedzie wadliwa
P(A/B2)− prawd. ze wylosowana zarowka z zakladu 2 bedzie wadliwa
P(B1/A)− prawd. ze wadliwa zarowka bedzie z zakladu 1
P(B2/A)− prawd. ze wadliwa zarowka bedzie z zakladu 2
28 gru 03:08
ZKS:
A co do zadania to trzymajcie:
| | 252x | | 99 | |
250x + 2 * 249x + ... + 49 * 22x + 50 * 2x = |
| + |
| . |
| | (2x − 1)2 | | 4 | |
Trzeba rozwiązać równanie
28 gru 03:09
kylo1303: "Znamy wynik doświadczenia, zatem skorzystamy z wzoru Bayesa."
To ja tego wzoru nie znalem, musialem na piechote wyprowadzac ale wyjdzie na to samo.
28 gru 03:09
Pepsi2092: Dzieki
ZKS ja ogólnie to jestem w technikum mam matme na podstawie i teraz zostało mi
jeszcze tak przysiąść bardziej nad prawdopodobieństwem i stereometrią i biorę się za powtórki,
narazie robiłem z Kiełbasy bardzo dużo to wydaje mi się że z panimetrią trochę tam przesadzili
w tej książce ale to może tylko moje wrażenie
Z innymi działami jest w miarę
tak czy tak
będę starał się robić jak najwięcej zadań bo matura już za 4 miechy
I licze na zadania z
dowodami z twojej strony bo to jest chyba mankament większości i jak czytają i widzą zadanie
Wykaż, albo uzasadnij to włos się jeży na głowie
28 gru 03:10
Basiek: Kylo Dziękuję, już jasne
Dobrze tłumaczysz.
ZKS− czepiasz się. A nie powinieneś.
28 gru 03:12
ZKS:
Nie czepiam się a powinienem.
28 gru 03:14
ZKS:
A masz jakieś z wykaż/udowodnij zadanie
Pepsi2092?
28 gru 03:15
Pepsi2092: Tak na teraz to nie mam żadnych zadań z wykazywaniem i udowadnianiem, chociaż przytrafiło mi
się kilka w mojej edukacji podczas ostatniego miesiąca takich że były spore problemy i jutro
poszukam bo już nie pamiętam dokładnie w którym zbiorze, ale wrzucę napewno
Mam jeszcze
zadania z poprzednich edycji Olimpiady o diament Agh więc jak bedę miał problemy (a czuję że
przy niektórych będą) to wrzucę
A w tym równaniu to tam po 2*2
49x to jest potem
3*2
48x itd czy jakaś inna reguła obowiązuje ?
28 gru 03:22
kylo1303: ZKS To twoje zadanko dosyc trudne, ale mysle ze jestem na dobrym tropie. Tyle tylko ze juz
ide spac, bo jutro z rana na hale ide pograc w pile a chce byc w miare do zycia. Napisze tylko
w skrocie moj tok rozumowania:
1. pomnozylem przez 2x
2. odjalem jedno rownanie od drugiego
3. jest mozliwosc zastosowania wzory na sume ciagu geometrycznego, co zastapi nam spora czesc
wyrazow.
Na tym etapie co jestem to juz powoli sie cos konkretnego ksztaltuje, ale dokoncze jutro to
najwyzej napisze.
28 gru 03:22
28 gru 03:25
ZKS:
Taka jest reguła jak piszesz
Pepsi2092 2
50x + 2 * 2
49x + 3 * 2
48x itd.
28 gru 03:25
Basiek: Zaczynam się robić głodna...
Dobranoc
Kylo
No i ja też idę, do kiedyś tam
28 gru 03:26
ZKS:
Ja też zrobiłem się głodny.
Dobranoc!
28 gru 03:30
Pepsi2092: No Dobranoc
kylo i
Basiek A co do równania to kurcze nie wiem narazie
jakby
wyłączyć 2
x to raczej nic nie da bo przy mnożeniu liczb o takich samych podstawach wykładniki
się dodaje
Pomyslę jeszcze chwilę
28 gru 03:30
Pepsi2092: Dobranoc Mistrzu
Jak się nie wkurzysz to wrzucę Ci jedno zadanie do sprawdzenia na jutro
28 gru 03:32
ZKS:
2
x wyłączenie nic nie da chyba że ktoś to tak zrobi po swojemu że jakoś wyjdzie.
A pomyśl
po to zadnie wam dałem żebyście mogli przemyśleć jak je rozwiązać.
28 gru 03:32
ZKS:
Daj teraz zadanko bo ja za parę chwil będę szedł na spanko więc jest jeszcze chwila czasu.
28 gru 03:34
Pepsi2092: log
9cos
11π6 − log
9sin
29π6 = log
9cos330 − log
9sin870 = log
9cos(360−30) −
log
9sin(900−30)= log
9cos30 − log
9sin30 a sin w II ćwiartce jest dodatni a cos w IV więc
będą +
i log
9 √32 − log
9 12= log
9 √32*2= log
9 √3=
14
9
x=3
12
3
2x=3
12
2x=
12
x=
14
Jak będziesz miał chwilę jutro
ZKS to możesz sprawdzić
Ja też uciekam spać
Dobranoc
wszystkim
28 gru 03:46
Pepsi2092: nad tym równaniem przysiądę dzisiaj jak wróce ze szkoły bo do 7 i tak się nie wyśpię dlatego
uciekam i sorry że tak narobiłem smaku z tym zadaniem ale mi chodziło o sprawdzenie ale masz
tutaj takie jedno bo czuje ze moga byc z nim problemu na pierwszy rzut oka
Dla jakich m proste mx+(m+1)y=2 i 4x+(m+4)y=1 przecinają się w punkcie leżącym wewnątrz II lub
IV ćwiartki układu współrzednych ?
Dobranoc
ZKS do dzisiaj
28 gru 03:52
ZKS:
wszystko jest dobrze.
28 gru 04:01
ZKS:
Wyznacznikami proponuję zrobić układ równań.
II ćwiartka to x minus y plus , IV ćwiartka to x plus y minus więc dla
II ćwiartki x < 0 ∧ y > 0
IV ćwiartki x > 0 ∧ y < 0.
28 gru 04:05
wik_gg8947201: Zadanie (pp)
Cegla wazy kilo i pol cegly. Ile wazy cegla?
28 gru 08:23
Basiek: 2kg
Dzień dobry wszystkim w ten piękny poranek
28 gru 10:54
ysiulec: Ile początkowych wyrazów ciągu arytmetycznego 5, 8, 11 ... należy dodać, aby otrzymać liczbę
185?
28 gru 11:02
ysiulec: dla Basiek zadanie
28 gru 11:02
Basiek: Wybacz, zaznajamiałam się z odkurzaczem
n=10
28 gru 11:27
rumpek: należy dodać a
1, a
2 ... a
9, a
10
gdzie a
10 = 32
28 gru 11:43
Basiek: Przykro mi,
Rumpek, nie mam dla Ciebie nic trudnego na miłe rozpoczęcie dnia.
28 gru 11:54
rumpek: Za to dla Ciebie
Basiek mam coś banalnego
Wybierz odpowiedni znak ze zbioru : =, <, >,
√(3)2 √(−3)2
będę za 3h jak cos
28 gru 12:18
Basiek: = ?
I3I=I−3I
3=3
28 gru 12:19
Basiek: Jak ktoś może, to ja jeszcze poproszę
5 zadanek z planimetrii − poziom podstawowy
Dziękuję.
28 gru 12:35
AC:
Niestety nie z planimetrii ale spróbuj je rozwiązać.
Dla jakich wartości parametru "m" równania:
2x2 − (3m + 2)x + 12 = 0
oraz
4x2 − (9m −2)x + 36 = 0
maja wspólny pierwiastek ?
28 gru 13:36
Basiek: AC Niedawno zauważyłam, dzięki za zadanko...
niestety nie mam pojęcia, jak się za nie zabrać− jakaś podpowiedź?
28 gru 14:07
rumpek:
2x
2 − (3m + 2)x + 12 = 4x
2 − (9m − 2)x + 36
na jedną stronę i chyba taka podpowiedź starczy
28 gru 14:22
Basiek: Dobra, nie, to nie
wolfram obliczył mi, że
m=3,
x=4
28 gru 14:22
Basiek: Wpadłam sobie już na to
Tylko policzyć, to ja dalej tego jakoś nie umiem
28 gru 14:23
rumpek:
2x
2 − 3mx −2x + 12 − 4x
2 + 9mx − 2x − 36 = 0
−2x
2 + 6mx − 4x − 24 = 0
−2x
2 + (6m − 4)x − 24 = 0 / * (−1)
2x
2 − (6m − 4)x + 24 = 0 / : 2
x
2 − (3m − 2)x + 12 = 0
i z tego można zapisać (aby były same plusy)
x
2 + (2 − 3m)x + 12 = 0
i tylko Δ = 0
28 gru 14:32
AC:
No co dalej rumpek?
Dostaniesz inny wynik niż Basiek
28 gru 14:39
Basiek: Doszłam do podobnej postaci, tylko hm, nie wiedziałam, co dalej.
Znaczy, nie wiedziałam, że Δ=0, no i nie bardzo wiem, czemu
Tzn. już rozumiem, ale sama bym na to raczej nie wpadła
28 gru 14:39
rumpek: No liczyć to mi się tego nie chce
ale dla Δ = 0 będą miały jeden wspólny pierwiastek
28 gru 14:41
Basiek: Z
Rumpka wywodów wynika, że
28 gru 14:43
AC:
Jak policzysz to wyjdzie Ci:
| | 2 | | 4 | |
Δ=0 ⇒ (3m−2)2 = 48 ⇒ 3m−2 = ±4√3 ⇒ m= |
| ± |
| √3 |
| | 3 | | 3 | |
i jak to się ma do m=3 Wolframu?
28 gru 14:44
Basiek: Halo, ja tu umrę z niewiedzy i ciekawości.
28 gru 14:53
rumpek: na pewno m = 3?
AC masz odpowiedzi do tego?
28 gru 14:59
28 gru 15:03
rumpek: sprawdź dla m = 2
co ci wyjdzie
28 gru 15:04
Basiek: Ech, Rumpek zmartwię Cię, to COŚ ma 5 rozwiązań. Nawet nie wiem, jakim cudem.
28 gru 15:06
Basiek: Godzio− a Ty?
28 gru 15:27
Godzio:
Właśnie zerknąłem do tematu i nawet nie mam zamiaru tego wszystkiego czytać, więc powiedz w
czym rzecz
28 gru 15:37
Basiek: W tym:
Dla jakich wartości parametru "m" równania:
2x
2 − (3m + 2)x + 12 = 0
oraz
4x
2 − (9m −2)x + 36 = 0
maja wspólny pierwiastek ?
Wolfarm pokazuje coś innego niż wychodzi... swoją drogą− on pokazuje 5 całkowitych rozwiązań,
nam wychodzą 2 niewymierne
28 gru 15:39
rumpek: Lub mi wychodzi m = 2 ale innym sposobem (z przyrównania x
w = x
w )
28 gru 15:43
ZKS:
Wstawić za x "m" do obydwu równań i później porównać.
28 gru 15:44
Godzio:
Ten sposób
f(x) = g(x) i Δ = 0 nie daje poprawnego rozwiązania ?
28 gru 15:44
ZKS:
Mi wszyło m = −2 i m = 3.
28 gru 15:45
rumpek: własnie nie
tak twierdzi AC
28 gru 15:45
Basiek: ZKS z jakiej okazji tak? : O
28 gru 15:46
Godzio:
2(x − x
1)(x − x
2) = 2(x
2 − x(x
1 + x
2) + x
1x
2)
4(x − x
1)(x − x
3) = 4(x
2 − x(x
1 + x
3) + x
1x
3)
| | 3m + 2 | |
−2(x1 + x2) = − (3m + 2) ⇒ x2 = |
| − x1 |
| | 2 | |
x
1x
2 = 12
| | 9m − 2 | |
−4(x1 + x3) = −(9m − 2) ⇒ x3 = |
| − x1 |
| | 4 | |
x
1x
3 = 36
Więc mamy układ równań:
A on chyba jest prosty do rozwiązania hm ?
28 gru 15:49
Godzio: Tylko że trzeba rozpisać wszystkie przypadki i dziedziny dla m
28 gru 15:49
ZKS:
f(x) = 2x
2 − (3m + 2)x + 12
g(x) = 4x
2 − (9m − 2)x + 36
f(m) = 2m
2 − 3m
2 + 2m + 12
g(m) = 4m
2 − 9m
2 + 2m + 36
f(m) = g(m)
−m
2 − 2m + 12 = −5m
2 + 2m + 36
4m
2 − 4m − 24 = 0
m
2 − m − 6 = 0
(m + 2)(m − 3) = 0 ⇒ m = −2 ∨ m = 3.
28 gru 15:50
Godzio:
Masz do tego odpowiedź?
28 gru 15:50
Basiek: Jeśli to było do mnie, to nie
Zadanie dostałam w ramach "masz, zrób zadanie z podstawy" od
AC
28 gru 15:55
28 gru 15:57
ZKS:
Albo wyznaczyć m i później wstawić do równań?
| | 2x2 − 2x + 12 | |
2x2 − (3m + 2)x + 12 = 0 ⇒ m = |
| |
| | 3x | |
| | 4x2 + 2x + 36 | |
4x2 − (9m −2)x + 36 = 0 ⇒ m = |
| |
| | 9x | |
| 2x2 − 2x + 12 | | 4x2 + 2x + 36 | |
| = |
| |
| 3x | | 9x | |
6x
2 − 6x + 36 = 4x
2 + 2x + 36
2x
2 − 8x = 0
x
2 − 4x = 0
x(x − 4) = 0 ⇒ x = 4 bo x ≠ 0 nie należy do dziedziny.
28 gru 15:59
Basiek: ZKS Teraz by się zgadzało, tylko zachodzę w głowę, czemu wszystkie inne rozwiązania dają
błędne wyniki.
28 gru 16:02
ZKS:
| | 2 * 42 − 2 * 4 + 12 | |
m = |
| |
| | 3 * 4 | |
m = 3
Więc wychodzi że dla m = 3 jest wspólny pierwiastek.
28 gru 16:05
Basiek: 
28 gru 16:07
ZKS:
Basiek może chcesz jakieś kolejne zadanko?
28 gru 16:11
Basiek: Przepraszam, muszę znikać
WIeczorem−póóźno
28 gru 16:19
ZKS:
Tak tak na pewno.
28 gru 16:22
Pepsi2092: Siemano
ZKS ,
Basiek i reszta
Nie pomyśl sobie że zapomniałem o Twoim zadaniu
ZKS Nie mam narazie pomysłów za bardzo ale zaraz przysiadam i dopóki nie zrobie nie
odejdę
Chodzi mi o wczorajsze równanie z tymi potęgami
28 gru 16:58
AC:
Zadanie z potęgami.
Jeśli się nie pomyliłem to
28 gru 20:10
kylo1303: ZKS Zadanie z "28 gru 03:09"
(to juz sama koncowke napisze)
200=−299*2
x+299
28 gru 20:18
kylo1303: To moze niech ZKS napisze jaka jest odpowiedz, bo ladne liczby to raczej nie wyjda...
28 gru 20:19
kylo1303: Dodam tylko ze z tej postaci do ktorej ja doprowadzilem wynika ze twoj x2 nie moglby spelniac
tego rownania (tylko co z tego jak i tak nie ma mozliwosc sprawdzenia). Przy czym tez moglem
sie pomylic w obliczeniach bo bylo tego sporo.
28 gru 20:25
ysiulec: No to takei zadanko z planimetrii:
W trójkącie ABC poprowadzono dwie proste równoległe do boku AB. Podzieliły one trójkąt na trzy
figury o równych bokach. Obliczyć długości odcinków, na jakie te proste podzieliły bok AC,
jeśli ma on długość 3√3
28 gru 20:39
kylo1303: "Podzieliły one trójkąt na trzy figury o równych bokach." nie do konca rozumiem sens tego
zdania
28 gru 20:57
ZKS:
kylo1303 niestety ale podana odpowiedź jest nie poprawna rozwiązuj dalej.
29 gru 02:29
Pepsi2092: ZKS ja tez wymiękłem
A co proponujesz w tym zadaniu?
Oto treść : Wykaż, że suma
odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy
obwodu trójkąta
Ryje mi głowe trochę na spółke z tym przykladem co nam podałeś
29 gru 02:35
ZKS:
Przepraszam ale jestem wczorajszy nawet nie trochę a bardzo.
Ale pomału dochodzę do siebie.
Z geometrii bym musiał sporo siedzieć żeby coś ogarnąć ale w dzisiejszym stanie ciężko mi
robić ogólnie coś.
29 gru 02:39
Basiek: Hm, mogę się wtrącić?
29 gru 02:42
ZKS:
Oczywiście że możesz.
29 gru 02:43
Basiek: Bo jak widzę "trójkąt", "połowa obwodu" to ja bym porównała pole z tego wzoru na pole Δ , gdzie
występuje obwód z polem Δ jako sumy trzech mały trójkątów, wiecie ah1/2 +bh2/2 +ch3/2
Taka propozycja na gorąco, liczyć mi się nie chce.
29 gru 02:46
ZKS:
Pepsi2092 a gdybyś tak po zapisywał nierówności odległości od punktów i później dodał
stronami chociaż nie wiem czy myślę poprawnie teraz.
29 gru 02:47
29 gru 02:50
ZKS:
Odległości tych punktów sobie oznaczymy d , e , f natomiast boki a , b , c.
a < d + e
b < d + f
c < e + f
−−−−−−−−−−−−−(
+)
a + b + c < d + e + d + f + e + f
a + b + c < 2d + 2e +2f
| a + b + c | |
| < d + e + f. |
| 2 | |
29 gru 02:50
ZKS:
O właśnie
Basiek o to mi chodziło.
A jak tam idzie rozwiązywanie równania wam?
29 gru 02:51
Basiek: Po primo− te pola mi się skojarzyły, bo pamiętam, w Pazdro klasa 1 lub 2ga było takie, tylko
był bodajże czworokąt i było JEST równe połowie obwodu. Na sprawdzianie akurat umiałam, ale
zamiast punkt zewnątrz przeczytałam wewnątrz i 0 pkt
ZKS JAKIE równania?
29 gru 02:57
ZKS:
| | 252x | | 99 | |
250x + 2 * 249x + ... + 49 * 22x + 50 * 2x = |
| + |
| . |
| | (2x − 1)2 | | 4 | |
29 gru 03:00
Basiek: Mam takie wrażenie, że jak to podawałeś− bodajże wczoraj−to byłam zajęta czym innym
stwierdziłam więc, że zad. to jest dla Pepsi/ Kylo albo obu. Wyobraź sobie, że ja jestem
niemal pewna, że tak było, więc mi nie wpieraj, że czegoś nie zrobiłam
29 gru 03:02
ZKS:
Basiek mam dla Ciebie trochę łatwiejsze zadanie.
| | 1 | | 1 | |
Oblicz x2 + |
| gdy x3 + |
| = 110. |
| | x2 | | x3 | |
29 gru 03:03
Basiek: Widziałam to w Podkowie
Rozdział pierwszy.
Tylko jak to się Boziu robiło..
29 gru 03:04
ZKS:
Ja Ci niczego nie wpieram rozumiem może byłaś zajęta czym innym nawet słowa nie napisałem że Ci
coś mówiłem o tym.
29 gru 03:05
ZKS:
To akurat zadnie z Aksjomatu ale również może było i w Podkowie.
29 gru 03:05
Basiek: Najlepszą obroną jest atak
Cóż, działa.
29 gru 03:06
ZKS:
Basiek dzisiaj traktuj mnie ulgowo bo ja tak średnio wszystko rozumiem teraz.
29 gru 03:09
Basiek: To jest nas dwóch ^^
29 gru 03:09
ZKS:
A to czemu nie robisz zadań tylko balujesz?
29 gru 03:10
Basiek: Eeee, świętowałam swoje urodziny
Jak to szło − "Pij, Baśka!"
29 gru 03:11
ZKS:
Uuu a o nas z forum zapomniałaś
Basiu nie ładnie.
Ale to klasowa czy rodzinna imprezka?
29 gru 03:13
Basiek: Klasowa
Na rodzinnej to raczej wyglądałoby troszkę inaczej. ^^ I wcale nie zapomniałam.
29 gru 03:14
ZKS:
Po klasowej to powinnaś zadanko podane przeze mnie rozpykać w minutkę.
A tylna część ciała
nie boli od paska?
29 gru 03:16
Basiek: Siadłam na podłodze i powiedziałam, że albo lekko, albo ja się tak nie bawię. Bowiem ja mogę
tak siedzieć do rana.
Więc nic mnie nie boli, o dziwo nawet głowa w porządku
29 gru 03:18
ZKS:
To uprzejmych masz kolegów i koleżanki raz się ma 18 − naście lat więc mogli nie żałować heh
żartuję oczywiście.
Jak nic nie boli to dobrze.
29 gru 03:22
Basiek: Nie tyle uprzejmi, co potrafię być autorytatywna.
Jak bardzo chcę, to potrafię postawić na
swoim
29 gru 03:23
ZKS:
To teraz zadanie czeka na rozwiązanie
Basiu.
29 gru 03:25
Basiek: doszłam do postaci
myślę nad czymś jak delta, czy coś. Nie wiem zresztą
29 gru 03:27
ZKS:
teraz szukaj pierwiastków w dzielnikach wyrazu wolnego.
29 gru 03:30
29 gru 03:33
ZKS:
Matura zaliczona na 5.
Mam jeszcze takie coś:
| 1 | | √3 | |
| − |
| = 4 Udowodnić równość. |
| sin10o | | cos10o | |
29 gru 03:36
Basiek: Nienawidzę trygonometrii. Mogę pomyśleć jutro?
29 gru 03:41
ZKS:
Eee tam jutro.
Spróbuj dzisiaj podpowiem oczywiście tylko zapisuj co i jak po kolei robisz.
29 gru 03:42
Basiek: | | 1*cos10−√3sin10 | | 1 | |
= |
| ={tu jeszcze myślę}{ |
| sin20} |
| | sin10*cos10 | | 2 | |
√3 mogłabym zamienić na tg60, a 1 na sin90, ale chyba nie widzę sensu
29 gru 03:47
ZKS:
Pomnóż obustronnie prze sin10
ocos10
o.
29 gru 03:49
Basiek: Hm, czyli przyjmuję, że całe równanie jest prawdą, a potem posługuję się całością i dochodzę do
jakiejś tożsamości?
29 gru 03:52
ZKS:
Oczywiście możesz robić na całym wyrażeniu przekształcenia aż dojdziesz do prawdy lub
przekształcając lewą lub prawą stronę.
29 gru 03:55
Basiek: Moja matematyczka pewnie kazałaby napisać do tego uzasadnienie, na próbnej to ja tam w sumie
opowiadaniami się zajęłam
hm, czyli
cos10−
√3sin10=4sin10cos10
no nie no
w zasadzie i tak nie wiem, co dalej ;[
29 gru 03:59
ZKS:
Obustronnie dzielimy przez 2 i po prawej stronie stosujemy wzór 2sinxcosx = sin2x a po lewej
stosujemy wzór sinxcosy − sinycosx = sin(x − y).
29 gru 04:03
Basiek: hm, naaa pewno wpadłabym na podzielenie przez 2...
| 1 | | √3 | |
| cos10− |
| sin10= sin20 |
| 2 | | 2 | |
sin30cos10−cos30sin10=sin20
sin(30−10)=sin20
sin20=sin20
L=P
cnu.
Ekhem, dzięęękuję
29 gru 04:08
ZKS:
Widzisz teraz już będziesz wiedziała jak się zabierać za takie przykłady.
Na zdrowie.
To takie ostatnie do sprawdzenia czy już załapałaś jak takie zadania robić.
Mamy funkcję f(x) = cosx −
√3sinx i trzeba rozwiązać równanie f(x) = 1.
29 gru 04:12
Basiek: Ty jesteś niezmordowany O.o
Ale popatrz. wszystkie grzeczne dzieci już śpią !
29 gru 04:13
ZKS:
Ojj i tak nie zasnę na tę chwilę.
A wolę na coś pożytecznym spędzić ten czas.
29 gru 04:15
Basiek: cosx−
√3sinx=1 /:2
I tu...eee
sin(30−x)=sin30
x=0 ? O,o
29 gru 04:17
Basiek: Ty może nie, Twój utylitaryzm jest no... wielki i na pewno pożyteczny, ale ja muszę wstać z
samego rana, posprzątać i napisać eight essays
29 gru 04:18
ZKS:
W porządku dalej mamy:
| | π | | π | |
sin(x − |
| ) = −sin( |
| ) |
| | 6 | | 6 | |
| | π | | π | | π | | π | |
x − |
| = − |
| + k * 2π ∨ x − |
| = π − |
| + k * 2π. |
| | 6 | | 6 | | 6 | | 6 | |
I teraz trzeba dokończyć.
Rozumiesz wszystko czy coś wytłumaczyć?
29 gru 04:23
Basiek: hm, jedno.
| | π | | π | |
Czy mogłabym zostawić sin( |
| −x) =sin( |
| ) |
| | 6 | | 6 | |
A potem sobie dalej rozpatrywać− i wyjdzie mi to samo bez tego przekształcania, tak?
29 gru 04:28
ZKS:
| | π | | π | |
Nie możesz zostawić sin( |
| − x) = sin( |
| ) bo nie wiemy dla jakich x jest spełniona ta |
| | 6 | | 6 | |
nierówność (oczywiście jedno rozwiązanie widzimy od razu że wynosi 0 ale brakuje nam tego
drugiego rozwiązania).
I oczywiści drugie rozwiązanie to:
| | π | | π | |
x − |
| = π + |
| + k * 2π. |
| | 6 | | 6 | |
29 gru 04:32
ZKS:
Jej już mówię głupoty nie nierówność tylko równanie oczywiście widzę że wracam do normalnego
stanu.
29 gru 04:34
Basiek: łapię, łapię, ale Ty po kilku przekształceniach dochodzisz do postaci:
| | π | | π | |
sin (x− |
| ) ja chciałabym to zostawić w postaci sin( |
| −x), pytałam, czy jak wszystko |
| | 6 | | 6 | |
potem ładnie uwzględnie, to będzie ok?
29 gru 04:35
ZKS:
| | π | | π | |
Oczywiście że możesz zostawić to w postaci sin( |
| − x) = sin( |
| ) i przekształcać |
| | 6 | | 6 | |
wtedy będziesz musiała pomnożyć na sam koniec przez (−1) żeby pozbyć się tego − przy x.
29 gru 04:37
Basiek: Albo poprzenosić
Okej, już wszystttko wiem, oprócz tego jak ja rano niby wstanę. Widzę, że
ICSP gdzieś tu
też krąży i myśli, ze jest niezauważony− jakbyś naaaprawdę nie mógł zasnąć, to pewnie podzieli
się z Tobą jakąś planimetrią,czy czymś
Ja znikam,
dobranoc i dziękuję
29 gru 04:39
ZKS:
Chciałem tylko pokazać że tego minusa przy x można się pozbyć w trakcie jak już dojedziesz do
wprawy to od razu będziesz się pozbywała go bo ja chciałem Ci tutaj pokazać żebyś zrozumiała
jak się pozbyć tego minusa krok po kroku żeby było jasne
29 gru 04:39
29 gru 04:41
Basiek: To miło, naprawdę
Jednakże mam tendencję do robienia wszystkiego na odwrót
a trygonometrii
chyba i tak nigdy do końca nie pojmę
29 gru 04:41
Basiek: Mój dar przekonywania jest doprawdy ogromny!
PS. Od jutra wracam do mojej programowej kombinatoryki i do powtórek z Cewą
29 gru 04:42
ZKS:
Też nie rozumiałem trygonometrii ale się uparłem na to i zrozumiałem więc wszystko przed Tobą
aby zrozumieć dobrze ten dział bo jest nawet fajny szczerze mówiąc (tylko nie wiem czemu
planimetrii i stereometrii nie polubiłem).
29 gru 04:44
ZKS:
Ja mam szczęście bo spotkałem kolegę i powiedział żebym mu przesłał tylko wymiary przekroju
parteru to mi to zrobi w programie i będę mógł przerysować tylko.
Życie jest jednak dobre .
29 gru 04:46
ZKS:
To jeszcze raz dobranoc bo jakoś za chciało mi się ciepłego łóżeczka.
29 gru 04:48
Basiek: Branoc
I miłego przerysowywania ^^
29 gru 04:48
ZKS:
Szybowania.
Jeżeli będziesz chciała jutro jakieś zadanka to napisz w tym czy innym poście to
jakieś dla Ciebie znajdę i nie zapominaj o równaniu które wyżej podałem.
Dobranoc.
29 gru 04:52
ICSP: Już wszyscy poszli spać ?
29 gru 05:07
kylo1303: ZKS Dzisiaj nie mam czasu ale jutro (albo dzisiaj w nocy) napisze ci moje rozumowanie co
do tego rownania, po prostu nie znalazlem bledu wiec napisze tutaj i wy sie tym zajmiecie xD
Nie wiem dlaczego, ale tutaj to chetnie zagladam, ale zeby otworzyc ksiazki i stamtad robic
zadania to juz nie bardzo
29 gru 17:56
Basiek: Zadanko na dobranoc?
29 gru 23:28
Godzio: A co z moją liczbą "p" ? Zrobione w końcu czy nie ?
29 gru 23:33
Basiek: Godzio albo z moją pamięcią coś nie tak, albo z Twoją. Nie dodawałeś tego zadania w jakimś
innym temacie?
No i nie mnie przy okazji?
29 gru 23:34
Godzio: Tobie pisałem, ale może jednak w innym temacie:
Znaleźć wszystkie takie liczby pierwsze p takie, że p2 + 13 jest też pierwsza
29 gru 23:36
Basiek: Kylo, Kasi lub Pepsi
Nie wpieraj mi, że mnie
Uwierz, pamiętałabym.
PS. Truuudne.
29 gru 23:37
Godzio:
Banalne
29 gru 23:39
Basiek: Ech...
Godzio , nie ta liga
29 gru 23:41
Godzio:
Zastanów się
29 gru 23:42
rumpek: Chcesz banalne? Proszę:
Udowodnij, że liczba n
7 − n jest podzielna przez 7
29 gru 23:45
Godzio:
Po pierwsze, mam nadzieję, że wiesz co to jest liczba pierwsza, podstawiaj po kolei te liczby
pierwsze i sprawdzaj co się dzieje, zauważ coś i to sformułuj
29 gru 23:46
Basiek: Hm, czekaj
Staram się...
czyli 1) suma musi być liczbą nieparzystą
2) 13− nieparzysta, czyli p
2 − parzysta
3) kiedyś p
2 jest parzyste? − kiedy p jest parzyste...
żadna liczba parzysta ZA WYJĄTKIEM 2 nie jest liczbą pierwszą.
Odp:
2
?
29 gru 23:46
Godzio:
Trudne ?
29 gru 23:48
Basiek: W zasadzie proste było. Ale jak widzę, że trzeba coś wymyślić, to rejteruję zanim zacznę
29 gru 23:49
Godzio: Dobra czekaj, coś ciekawszego może znajdę
29 gru 23:51
Basiek: eeee, ciekawszego to może nie?
29 gru 23:52
Godzio: Weźmiemy takie ciekawsze, rozluźniające
Znaleźć taką najmniejszą liczbę naturalną n, aby liczby postaci n + 1 oraz n − 110 były
kwadratami liczb naturalnych
29 gru 23:53
toja:
Załóżcie nowy "kącik" ......... bo przewijanie trwa dłużej niż rozwiązanie
29 gru 23:56
Godzio:
Hmm, ja mam tak, że jak wchodzę, to od razu mnie na sam dół przerzuca
29 gru 23:57
Basiek: Ja już się zadomowiłam
Witaj,
Toja
29 gru 23:58
toja:
Hmmm ....... bo jesteś młody
29 gru 23:58
toja:
ok
Witaj "zadomowiony"
Basiek
30 gru 00:00
Basiek: n=399
?
30 gru 00:05
Godzio:
Ale to masz pokazać, że tak jest, a nie sobie znaleźć
30 gru 00:07
Basiek: bo eeej, czepiasz się
30 gru 00:07
toja:
30 gru 00:08
Godzio:
Można to obliczyć najnormalniej w świecie (są 2 odpowiedzi
)
30 gru 00:08
Basiek: okej
a,b,n∊ℕ
{a2=n+1
{b2=n−110
a2−b2=111
(a−b)(a+b)=111
{a−b=3
{a+b=37
2a=40 ⇒ a=20 , b=17
400=n+1
n=399
30 gru 00:10
Godzio:
O to chodziło
A drugie n : D?
30 gru 00:11
Basiek: Ile lat jest za morderstwo z premedytacją?
30 gru 00:11
Godzio: Dla Ciebie dożywocie
30 gru 00:13
Basiek: ale dożywocie to długo
Odezwę się za 5 min (albo więcej)− jak znajdę cholerne drugie n
30 gru 00:14
Godzio: Ciąg an określony jest wzorem an=n2+pn+p, gdzie p ∊ R Wykaż, ,ze nie istnieje taka liczba
całkowita p, ze dwa wyrazy ciągu an są równe −3
30 gru 00:15
Godzio:
No ale
n = 17
2 + 110
30 gru 00:16
Basiek: No... 172 +110= 399
30 gru 00:18
Godzio:
Yyy czekaj
Coś namieszałem
30 gru 00:18
Godzio:
No dobra, zapytam tylko, sprawdziłaś inne przypadki ?
30 gru 00:19
Basiek: Godziooo! Ja tu już doszłam do liczby 111:53 (doszłam do 53 od 3−jki!)
Olaboga... przecież musi być jedna odpowiedź. Nie strasz mnie, co?
30 gru 00:20
Godzio:
a + b = 111
a − b = 1
Z tego nic nie wyjdzie ? (nie wiem, nie sprawdzałem
)
30 gru 00:22
Basiek: Przy takim ustawieniu a, b
przy a −> n=783
przy b−> n=6779
(chyba)
PS. Czy my wiemy, jaki to ciąg?
30 gru 00:24
Godzio:
Po prostu ciąg, ani arytmetyczny, ani geometryczny
Co do zadania
a + b = 111
a − b = 1
a = 56
b = 55
Jedno n wychodzi
skąd wzięłaś te 2 wyniki ?
30 gru 00:27
Basiek: Wiesz co?
Sama nie mam pojęcia, jak mogłam to tak wklepać w kalkulator,że wyszło całkiem coś
innego : O
Ale masz rację całkowitą. Ech
Pieskie życie
30 gru 00:29
Godzio:
Hmm ciekawe zadanie
Nie mam narazie pomysłu, kiedyś je robiłem, takie ciekawsze zadania
zapisuje sobie, żeby mieć na przyszłość
30 gru 00:35
Basiek: Co do tego ciągu... nie mam
zielonego pojęcia.
obliczyłam sobie p dla a
n=−3, ale nic mi to nie dało
Niestety to jedna z niewielu rzeczy,
jaką umiem zrobić z ciągami niewiadomego pochodzenia
http://www.maturzysta.info/pdf_portal/tematy_rozmaite.pdf Łap
Te "siedem ciekawych zad." naprawdę jest ciekawych
30 gru 00:40
Godzio:
Zaraz się zastanowię nad zadaniem, a za stronkę dzięki, przyda się
30 gru 00:44
Basiek: "Oblicz długość pasa w przekładni pasowej, mając dane długości promieni kół: 40cm i
10cm, oraz odległość środków tych kół równą 60 cm. "
Zanim dowiem się jak wygląda pas w przekładni pasowej, idę po kawę
30 gru 00:48
Godzio:
Zadanie z ciągiem bym tak rozwiązał:
a
n = − 3
| | −3 − n2 | | 4 | |
⇒ p = |
| = − n + 1 − |
| |
| | n + 1 | | n + 1 | |
p ∊ C ⇔ n = 1 lub n = 3, odpowiednio dla n, p = − 2 lub p = − 3
Dla p = − 2 mamy:
a
n = − 3 ⇒ n = 1
Dla p = −3 mamy:
a
n = − 3 ⇒ n = 0 lub n = 3 −− 0 oczywiście odpada, widzimy więc, że nie ma dwóch takich
wyrazów
30 gru 00:56
Basiek: Łaaadnie <3
No, ja bym na to nie wpadła w tym stuleciu
30 gru 01:00
Basiek: ZKS − jesteś?
30 gru 01:06
ZKS:
Tu i teraz. A co tam?
30 gru 01:12
Pepsi2092: Siema wszystkim i oczywiście szczególnie założycielce tego kącika Mrs
Basiek Czekam na
zadanko z dowodami takie na miarę poziomu rozszerzonego od
ZKS lub innego osobnika
30 gru 01:13
ZKS:
Widziałeś już to wcześniej a
4 − a + 1 > 0? Jeżeli nie to udowodnij nierówność.
30 gru 01:15
Basiek: ZKS − heeej
No otóż właśnie, świetnie, że jesteś
Miałeś mnie też dziś czymś pomęczyć
Czekam, czekam− a Ty chyba śpisz
I .. cześć
Pepsi
30 gru 01:16
Godzio:
To było jedno z pierwszych zadań ode mnie
ZKS
30 gru 01:19
ZKS:
To jest Twoje zadanie
Godzio uczniom będziesz je dawał do rozwiązania.
30 gru 01:22
Godzio:
No
30 gru 01:23
Pepsi2092: Dobra ja tego nie widziałem ale juz sie biore za rozwwiązanie więc niech żadna menda tutaj
publicznie narazie nie rozwiązuje
30 gru 01:24
ZKS:
Myślałem że już nie chcesz żeby Cię męczył
Basiek?
Ale jeżeli chcesz to znajdę dla
Ciebie zadanko.
30 gru 01:26
Basiek: Ja już swoje z tym zadaniem przeszłam, więc pozostawiam Ci je, Pepsi.
Btw. czy wiesz, co znaczy "menda"? Wydaje mi się, że nie, bo raczej byś tak tym słowem nie
szastał na lewo i prawo
30 gru 01:26
Godzio:
ZKS dla mnie możesz coś znaleźć
30 gru 01:27
Basiek: ZKS− PROSTE
wiesz, miałam wrócić do swoich "szkolnych" zadań, ale dziś nie wyszło.
Sprzątanie, angielski, kino...., cały dzień z głowy
więc cóż, z chęcią zrobię jakie
proste zadanko
, a do szkoły zacznę uczyć się ... jutro (?)
30 gru 01:28
ZKS:
Hmm "menda" to słyszałem że to takie miłe stworzonko jest.
30 gru 01:29
Godzio:
Ooo bujne życie ... moje skończyło się na śnie przez cały dzień
30 gru 01:29
Basiek: ZKS taaa, bardzo milusie
Myślę jednakże, że jest wiele ładniejszych zwrotów do
nadgorliwych użytkowników forum
Godzio A tam bujne życie, wprost przeciwnie. A w ogóle, to na calodzienny sen chętnie bym
się zamieniła <3
30 gru 01:31
ZKS:
a
2 + b
2 + c
2 ≥ ab + bc + ca.
Takie mam do udowodnienia dla Ciebie
Basiek. Chyba że chcesz jakiś szczególny dział to za
chwilkę poszukam czegoś?
30 gru 01:31
Godzio:
No nie wiem
14 − 23 sobie spałem
30 gru 01:32
ZKS:
Ja bym nie dał rady później bałbym się że w nocy nie będę mógł spać hehe.
30 gru 01:34
Basiek: Po pierwsze−
ZKS − trudne
Ale chociaż powpatruję się w kartkę, to bardzo kreatywne
Dziękuję.
Godzio − pff
nie ma się czym chwalić, przy mnie wymiękasz
30 gru 01:36
Godzio:
Jakie trudne, rozpisując super dokładnie w trzech przejściach max wychodzi
30 gru 01:37
ZKS:
Widzisz Twoje zadnie
Godzio jest bardzo ciekawe
Pepsi2092 coś długo nie pisze.
30 gru 01:39
rumpek: skąd ty
ZKS bierzesz te nierówności wszystkie
?
30 gru 01:40
ZKS:
A co
rumpek chcesz jakieś?
30 gru 01:42
Godzio:
ZKS za zamówienie wymyśla
30 gru 01:43
rumpek: ale na kiedyś tam
bo na dzisiaj już nie mam siły, a jutro "zamierzam" pisać biografię na
pracę maturalną z polaka
30 gru 01:44
rumpek: bibliografię*
30 gru 01:44
Basiek:
Godzio specjalnie dla Ciebie powyższy schemat.
G− Godzio
B−Basiek
P−proste
T−trudne
To koło to symboliczna granica− jak mur u Leśmiana.
PRZEANALIZUJ.
30 gru 01:45
ZKS:
Hehe.
30 gru 01:45
Pepsi2092: Chwila chłopaki chwila, bo myślę nad zadaniem a dodatkowo mnie męczą planami Sylwestrowymi na
fb
30 gru 01:45
ZKS:
Ale coś mogę Ci na szybko dać
rumpek więc Polski możesz zrobić innym razem.
30 gru 01:46
ZKS:
Jeszcze nie widziałem żeby ktoś zrobił zadnie
Godzio Twoje z tą nierównością każdy się
meczy z nią.
30 gru 01:48
rumpek: i tak zaraz idę w kimę bo o 6 trzeba wstać
, ale możesz dać zadanie podobne do poziomu jakie
dostała
Basiek
30 gru 01:48
Godzio:
@
rumpek Ja chyba 2 dni przed oddaniem to pisałem
@
Basie wierz mi, jak ja mówię, że coś jest proste to jest, (tak samo jak z p
2 + 13), a
jak coś trudniejszego to mówię, że trudne
To zadanie od
ZKS spokojnie na podstawę jest
30 gru 01:48
rumpek: Godzio ja musze oddać to do 5 stycznia
30 gru 01:49
Godzio:
ZKS ja też się z nim długo męczyłem, dostałem je od
Ety
30 gru 01:49
rumpek: a potem sylwester itp. nie bedzie czasu
30 gru 01:49
Basiek: @Rumpek− jaki temat ?
30 gru 01:50
rumpek: gdybym to ja pamiętał
ale coś w deseń " analizując wybrane utwory (od ośw. do renes.)
przedstaw postać Boga"
30 gru 01:55
ZKS:
a
4 + b
4 + c
4 ≥ abc(a + b + c). Takie coś dla Ciebie
rumpek.
30 gru 01:55
ZKS:
Ja miałem pracę z polskiego jak się nie mylę przedstawić stosunek człowiek do Boga.
30 gru 01:56
Basiek: Ależ mieliście wzniosłe tematy
Poruszające kwestię metafizyki i wiary
30 gru 01:57
rumpek: i jak był stres jak wszedłeś ?
Jak zdam z polaka to będzie mój wielki sukces
30 gru 01:57
Godzio:
Haha, coś nas łączy, moja to: literackie dialogi z Bogiem
30 gru 01:57
rumpek: a ty
Basiek jaki temat
?
ZKS chodzi ci o bardzo bardzo długą metodę czy taką średnią
?
30 gru 01:59
rumpek:
30 gru 01:59
Basiek: Eee, motyw dziecka w literaturze i malarstwie
?
30 gru 02:01
ZKS:
Jaką chcesz możesz podać dwa rozwiązania jeżeli masz.
Godzio widzisz coś nas łączy
przez Boga.
30 gru 02:03
rumpek: Na ile zdaliście ustną z polskiego
? Bo nią mało kto się chwali
30 gru 02:06
ZKS:
Godzio wiesz jak to rozwiązać?
30 gru 02:06
Godzio:
11
30 gru 02:06
ZKS:
14 punktów czyli 70%
.
30 gru 02:06
rumpek: Ale zdałeś
Ja to będę cieszył się z 30%
Przynajmniej nie dostane kosy z polaka
bo mam z
nią lekcje
30 gru 02:07
Basiek: Mój humanistyczny umysł pyta− jak można tego w ogóle nie zdać?
Btw. wiecie, że od 2015r. matura jest w wakacje, a ustny polski to LOSOWANE pytania z teorii
literatury oraz JĘZYKA.?!
30 gru 02:08
Godzio:
Powiedz coś więcej, w rzeczywistych to ma być spełnione ?
30 gru 02:09
ZKS:
A nie napisałem dla R+.
30 gru 02:10
ZKS:
A gdzie rozwiązane nierówności 3 dałem a na razie nie widzę żadnego rozwiązanego.
30 gru 02:11
rumpek:
wlasnie pytanie odnosnie mojej nierówności, w jakich liczbach?
30 gru 02:11
rumpek: mogę zrobić
Basiek bo się okazało że będę wykorzystywał ją w swojej
30 gru 02:12
Basiek: ech, to ja mam tak
wiemy, że
(a−b)2+(b−c)2+(c−a)2 ≥0
2(a2+b2+c2)−2(ab+bc+ca)≥0 /:2
a2+b2+c2≥ab+bc+cd
cnu.
30 gru 02:14
ZKS:
Nie wiem czemu na odwrót
Basiek to zrobiłaś tak jakoś po chińsku.
30 gru 02:16
Basiek: Faceci są okropni! Tak źle, tak niedobrze...
30 gru 02:17
rumpek:
a
2 + b
2 + c
2 ≥ ab + bc + ca / * 2
2a
2 + 2b
2 + 2c
2 ≥ 2ab + 2bc + 2ca
(a
2 − 2ab + b
2) + (a
2 − 2ac + c
2) + (b
2 − 2bc + c
2) ≥ 0
(a − b)
2 + (a − c)
2 + (b − c)
2 ≥ 0
Komentarz i z głowy
30 gru 02:18
Pepsi2092: Powiem Ci
ZKS że poszukuje współczynników w tym równaniu i nie wiem czy w dobrą strone idę
chcę zrobić coś w ten deseń (a
2−1+ coś)
2 = (a
2−1)
2 +2(a
2−1)* coś + coś
2 napisz mi
tylko czy w dobrą stronę idę
30 gru 02:18
rumpek: Pepsi2092 ja tam zrobiłbym z ułamkami
ale nie wiem czy
30 gru 02:20
Pepsi2092: Ja to myslałem, żeby tutaj nawet powrzucac jakieś
√a itd ale jeszcze próbuję
30 gru 02:22
ZKS:
Prawie w dobrą bo te (a
2 −
1)
2 tutaj bym coś innego dał zamiast tych jedynek i źle masz
tą dwójkę
2(a
2 − ?)
2.
30 gru 02:24
ZKS:
Basiek jak sobie znajdziesz chłopaka chyba że już masz to zobaczysz jacy jesteśmy
wspaniali hehe.
30 gru 02:25
Basiek: ZKS dzięki, jak jeszcze kilka razy usłyszę o potencjalnym mężu/ chłopaku, czy kimś tam, to
rzucę się z okna i będę pretendować do miana świętej.
A wspaniali?
Skarbie, z której strony?
30 gru 02:27
ZKS:
Na wesele zaprosisz mam nadzieje.
30 gru 02:32
Basiek: Haha, vice versa
Tylko Ty mojego możesz nie dożyć
30 gru 02:33
ZKS:
Nie planuję na razie niczego co by mogło skrócić mój żywot.
30 gru 02:39
Basiek: Co wcale nie zwiększa Twoich szans na uczestnictwo w moim ślubie.
Także z czystym sercem
mogę Cię zaprosić
30 gru 02:40
Godzio:
| a3 + b6 + 8 | |
| ≥ 3√a3b6*8 = 2ab2 |
| 3 | |
a
3 + b
6 ≥ 6ab
2 − 8 /:2
Teraz na to wpadłem, nie masz pojęcia jakie ja tu przekształcenia i wzory skrócenia 3 zmiennych
narobiłem i zawsze mi jeden wyraz zostawał
30 gru 02:44
Pepsi2092: Sorry, że przeszkadzam w planowaniu wesela, ale tutaj mam małe pytanie
Tą gotową postać
która będzie już wykazaniem tej nierówności to trzeba zapisać w formie (a
2−coś)
2 +
(coś+−coś)
2>0 czy (a
2−coś +−coś2)
2 >0?
30 gru 02:45
ZKS:
Odżywiam się zdrowo więc chyba dożyje do 200 lat i dostanę zaproszenie.
rumpek Pepsi2092 gdzie rozwiązanie nierówności?
30 gru 02:45
Pepsi2092: rumpek wariat to już zrobił, tylko ja kuleję na końcu jak zwykle
30 gru 02:47
ZKS:
Ta pierwsza forma
Pepsi2092.
Godzio widzę że naprawdę jesteś Profesorem dotyczących spraw z matematyki.
30 gru 02:48
ZKS:
rumpek nie zrobił nierówności którą mu podałem więc jeszcze zdążysz przed nim.
30 gru 02:49
Pepsi2092: oky to próbuję dalej
Nie chciałbym mieć takiego zadania na maturze, no chyba, że czas
wydłużą do jednego dnia albo bedę miał dostep do forum
30 gru 02:50
Godzio:
Zamilkli wszyscy, pewnie pozasypiali przed nierównościami
30 gru 03:04
ZKS:
Tak czasem bywa.
30 gru 03:17
Godzio: Spoko, o 5 rano wstaje
30 gru 03:28
Basiek: A opłaca Ci się kłaść?
30 gru 03:28
Godzio: Nie mam zamiaru iść spać
30 gru 03:34
Basiek: To chyba wstajesz z fotela...
30 gru 03:36
kylo1303: Witam wszystkich w ta piekna zimowa noc. Pierwsze pytanie to czy jest ZKS bo zaraz pomecze
sie i napisze moje rozwiazanie co do tego nieszczesnego rownania i bedziesz musial mi
wytknac blad. A te nierownosci ktore tutaj wyzej podaliscie to mozecie jeszcze raz dac bo nei
chce mi sie szukac a tez moge poprobowac.
30 gru 03:44
Godzio:
Jak coś to mogę coś sprawdzić co tu napiszesz
30 gru 03:45
Basiek: Cześć
Kylo, "zimowa" to złe określenie, jest całkiem ciepło
I hm, proponuję zadania jakoś zacząć zaznaczać, żeby się wyróżniały
30 gru 03:47
ZKS:
To
Godzio chcesz nierówność typu tego co Ci wyżej dałem jeżeli spać nie idziesz?
30 gru 03:54
Godzio: No możesz dać
30 gru 03:55
kylo1303: 2
50x+2*2
49x+...+50*2
x=a (prawa strone zastapilem a zeby ulatwic zapis)
2
50x+2*2
49x+...+50*2
x=a /mnoze przez 2
x
2
51x + 2*2
50x + 3*2
49x+...+50*2
2x=a*2
x
odejmuje stronami od drugiego pierwzse, zostaje mi:
2
51x+2
50x+*2
49x+...+2
2x−(50*2
x)=a(2
x−1)
2
51x+2
50x+*2
49x+...+2
2x + 2
x − (51*2
x)=a(2
x−1)
tutaj widac ze pierwsze 51 wyrazow tworzy ciag geometryczny o a
1=2
x i q=2
x, moge zastosowac
wzor na sume ciagu geometrycznego.
| 2x*(1−251x) | |
| − (51* 2x)=a(2x−1) z ulamka wylaczam minus i dziele przez (2x−1)
|
| 1−2x | |
| 252x−2x | | (51* 2x) | |
| − |
| =a (wylaczam z peirwszego ulamka "−2x")
|
| (2x−1)2 | | (2x−1) | |
| 252x | | 2x | | (51* 2x) | |
| − |
| − |
| =a (podstawiam pod a)
|
| (2x−1)2 | | (2x−1)2 | | (2x−1) | |
| 252x | | 2x | | (51* 2x) | | 252x | |
| − |
| − |
| = |
| + |
| (2x−1)2 | | (2x−1)2 | | (2x−1) | | (2x−1)2 | |
| 2x | | (51* 2x)*(2x−1) | | 99 | |
| + |
| =− |
|
|
| (2x−1)2 | | (2x−1)2 | | 4 | |
I tutaj juz szukajcie bledow, bo dalej to kiedys juz rozpisalem i bylo zle. Sory ze tak dlugo
ale sporo roboty przy czyms takim
30 gru 03:58
ZKS:
Dla ℛ
+ , a
2 + b
2 = 1 zachodzi:
a
3 + b
3 ≥
√2ab.
Proszę.
30 gru 03:59
Pepsi2092: Kurde już i tak za dużo wskazówek chyba dostałem
a i tak nie moge dojść do końca
Jak
zrobię (a
2+
1a)
2+ (.......)
2 >0 to nie wiem co wrzucic do tego drugiego nawiasu
30 gru 03:59
Pepsi2092: Sorry tam chciałem napisać (a
2−
1a)
2
30 gru 04:01
kylo1303: Przeksztalce lewa strone:
| | 2x+51*22x−51*2x | |
L= |
| = |
| | (2x−1)2 | |
| | 51*22x−50*2x | | 25*(22x−2*2x+1)+26*22x−25 | |
|
| = |
| =25 + |
| | (2x−1)2 | | (2x−1)2 | |
Tutaj kawalek ciagu dalszego ale juz widze gdzie mam blad, po prostu potem zapomnialem o
kwadracie w mianowniku
zaraz postaram sie to naprawic.
30 gru 04:08
Godzio: arytmetyczna ≥ geometryczna
a
6 + b
6 ≥ 2a
2b
2
oraz wiemy, że 2a
3b
3 > 0 więc po dodaniu mamy:
a
6 + 2a
3b
3 + b
6 ≥ 2a
2b
2
(a
3 + b
3)
2 ≥ 2a
2b
2
a
3 + b
3 ≥
√2ab
Gdzie tu się wykorzystuje, że a
2 + b
2 = 1
?
30 gru 04:12
Godzio:
A już ślepy jestem
30 gru 04:14
ZKS:
Za chwilkę pomogę może znajdziesz błąd ale najpierw
Pepsi2092.
(a
2 −
liczba)
2 + (a −
liczba)
2 +
inna liczba
liczba +
liczba +
inna liczba = 1
30 gru 04:14
Basiek: Godziu, jak będziesz mieć kiedyś czas, to wytłumaczysz mi, o co chodzi z tymi średnimi
? Dzięki.
30 gru 04:15
Godzio:
Ok
Ale tutaj źle zastosowałem
30 gru 04:17
kylo1303: kurde, doszedlem do rownania kwadratowego postaci:
303t
2−398t+99=0 gdzie t=2
x
Moglbym probowac rozwiazac ale nie wiem czy to mi cos da
30 gru 04:17
Basiek: Gdybyś się nie przyznał, pewnie nikt by nie zauważył
Poza tym, chyba widzę jak używasz tego
5−ty raz
I za każdym razem zachodzę w głowę, o co chodzi
30 gru 04:18
Pepsi2092: Dzięki
ZKS za cierpliwość i wskazówkę już o nic nie zapytam odnośnie tego rónania bo
wszystko ma swoje granice
No chyba że o to czy dobrze
30 gru 04:20
Basiek: Kylo coś musiało Ci chyba nie wyjść
t= {99}{101}
Z tą dwójką Ci nie pasuje.
Ktoś chyba musi znaleźć błąd
30 gru 04:20
ZKS:
Rozwiązanie jest w porządku. Gratuluję.
30 gru 04:23
ZKS:
Czyli x ile wynosi ostatecznie?
30 gru 04:24
kylo1303: Wlasnie zauwazylem ze √Δ to wyjdzie ladna liczba...
30 gru 04:24
Basiek: To teraz logarytmami?
30 gru 04:25
ZKS:
Tak.
30 gru 04:25
kylo1303: | | 1 | | 99 | | 99 | | 1 | |
(2x= |
| v 2x= |
| )⇒ x=log2 |
| v x=log2 |
| |
| | 3 | | 101 | | 101 | | 3 | |
30 gru 04:27
ZKS:
Aż takie trudne do ogarnięcia nie jest zależność między średnimi.
30 gru 04:27
kylo1303: A ten "wolfram" to pozyteczny jest bo nie korzystalem? Mozna liczyc tylko funkcje kwadratowe
czy wiele innych?
30 gru 04:27
Basiek: Wiele, wieeeele, wieeeeeeeeeele. Cudo po prostu.
30 gru 04:29
Godzio:
Wszystko można liczyć,
ZKS nie mam sił już nic robić
Więc na dzisiaj odpuszczam tą
nierówność
30 gru 04:30
kylo1303: Przynajmniej wymeczylem to zadanie od
ZKS teraz moge z czystym sumieniem pojsc spac,
chociaz jeszcze troche moze z wami posiedze. Za pierwszym razem zrobilem glupi blad (wiem, nie
ma madrych bledow) typu "przeoczenie", zdarza sie
30 gru 04:31
Pepsi2092: Chyba zrobiłem
ZKS ale z bardzo dużą pomocą
Wg mnie to takie coś
(a
2−
12)
2+(a−
12)
2 +
12>0 czy to tak ?
30 gru 04:34
kylo1303: Mozecie napisac jakas jedna nierownosc? Bo nie chce mi sie szukac (przepraszam za moje
lenistwo) xD
30 gru 04:34
ZKS:
Właśnie
Godzio co do zastosowania zależności między średnimi w tym zadaniu to jak piszesz
powinno być czy nie?
a
6 + b
6 ≥ 2a
3b
3 ?
30 gru 04:34
Godzio: No pisałem że źle zrobiłem
Ale nie mam sił
30 gru 04:35
Basiek: Kylo− w ogóle gratulacje, nawet szybko do tego doszedłeś
A jeśli już mowa o błędach, to
Godzio− co do tej n−ki na saamym początku dziś− trzeba było
znaleźć najmniejszą, a nie wszystkie możliwe (lubię się czepiać)
30 gru 04:35
ZKS:
Pepsi2092. Jakiego typu nierówność ma być
kylo1303?
30 gru 04:36
ZKS:
Heh czyli rozumiem zależności miedzy średnimi.
30 gru 04:37
Godzio:
Oj tam
30 gru 04:38
Basiek: Doczytałam, mogę iść spać
Dobranoc
30 gru 04:40
kylo1303: No nie wiem jakeigo typu, jakeis tutaj sie pojawily
W sumie po prostu chodzi mi o zadanie
(poziom liceum, rozszerzony) do rozwiazania, nie musi to byc koniecznie nierownosc ale zeby
nie bylo geometrii
30 gru 04:40
Pepsi2092: Ale jestem cienki w tych zadaniach od
ZKS, jak dupa węża
Ale przy nim wszyscy nabiorą
wigoru a ja razem z Wami
Jutro idę do szkoły więc uciekam a wieczorem znowu przyjdę po
jakiś dowód z wykazywania
Powodzenia dla reszty i jeszcze raz wielkie dzięki za cierpliwość
i podrzucone zadania
ZKS. Dobranoc dla najwytrwalszych
30 gru 04:43
ZKS:
Dla dodatnich zachodzi:
ab + bc + ca ≥
√3abc(a + b + c)
Takie łatwe.
Dobranoc
Pepsi2092 i
Basiek.
30 gru 04:46
Godzio:
Dobranoc
30 gru 04:48
kylo1303: Do jakiej szkoly on chodzi? Pierwszy raz slysze zeby ktos w swieta chodzil sie uczyc xD Zaraz
sie wezme do zadania
30 gru 04:48
ZKS:
Jutro do mnie ksiądz przychodzi bo mam kolędę o 9 rano hehe.
Za chwilę też będę kładł się na
spanie tylko poczekam na udowodnienie nierówności.
30 gru 04:53
kylo1303: (ac−ab)2+(ac−bc)2+(ab−bc)2≥0
30 gru 04:53
kylo1303: Ja jutro musze wstac o 10, dla mnie to i tak wczesnie (dzisiaj wstalem o 15.30), ale patrzac
tutaj po niektorych to i tak bede czul sie wyspany w porownaniu z wami
30 gru 04:55
ZKS:
. Idę na spanko.
Dobranoc
Godzio.
30 gru 04:58
Godzio: Dobranoc
30 gru 04:59
kylo1303: Dobranoc wszystkim, tez sie juz zabieram do spania.
30 gru 05:00
Basiek: Dzień dobry, wszystkim
Mam hm, bardzo głupie pytanie
| | 1 | |
Więc bla bla bla, n dla jakiego prawdopodobieństwo będzie > |
| |
| | 3 | |
Doszłam do postaci
Zachodzę w głowę, jak to obliczyć, bo chyba mi "uciekło"
30 gru 17:40
Pepsi2092: Hello
Basiek Ten kącik który załozyłaś jest nocny więc do 20 nikt nie powinien dawać
znaków życia
30 gru 19:08
Basiek: Cześć
Pepsi Zauważyłam, cóż... ale
Toja mi pomogła i powyżej już nieaktualne.
Swoją drogą, ja dziś idę spać o 22! Obudziłam się dziś o 17tej... Czas wrócić do normalnych
godzin bytowania
30 gru 19:18
Pepsi2092: Ja prawdopobobieństwa nawet nie ruszam narazie bo dopiero w połowie stycznia będe miał więc nie
pomogę
Basiek A co do spania to wiesz ja tez o 16 wstałem ale masz rację trzeba
zmienic tą japońską strefe czasu na normalność
30 gru 19:29
Basiek: Ech, dla mnie prawdopodobieństwo to rzeźnia jak rzadko. Załapałam urny itd., ale przy
tramwajach i szufladach moje szare komórki obumierają.
Niby coś jest logiczne, robisz sobie
robisz .... a wynik się nie zgadza.
Okazuje się, że jest "logiczniejszo−poprawniejsze"
rozwiązanie.
Nam została jeszcze statystyka i stereometria, więc jest jeszcze trochę roboty.
Ja sama muszę popracować nad: logarytmami, planimetrią, trygonometrią i stereometrią
[Troszkę tego jest]
A najbardziej lubię geometrię analityczną na płaszczyźnie <3
30 gru 19:38
Basiek: Odświeżam, żeby nie zaginął jutro
31 gru 00:01
Godzio:
Na rekord idziesz z postami
? Najdłuższy chyba miał kilka tysięcy
31 gru 00:05
Basiek: Czy Ty mi tu sugerujesz, że chcę kogoś zespamować, czy coś?
Nie ma sensu zakładać kilkuset postów, jeśli wszystkie tyczą się tej samej osoby i tego samego
tematu. Chyba. Jesteś innego zdania?
31 gru 00:07
Jordan: Za niedługo z rana będę musiał załączać posta żeby wieczorem odczytać ostatnią wiadomość
31 gru 00:37
Jordan: Za niedługo z rana będę musiał załączać posta żeby wieczorem odczytać ostatnią wiadomość
31 gru 00:38
Basiek: Jordan − witaj
Ciebie jeszcze nie znam.
Długo Ci wczytuje stronę, czy chodzi o przewijanie?
31 gru 00:39
Jordan: No dość trochę wczytuje
P.S sory za double ale za pierwszym razem wydawało mi się że wyślij nie reagowało
31 gru 00:45
Basiek: Wiesz, jakby Ci to łagodnie...
a)Jeśli Ci długo wczytuje −> masz za wolny internet , choć w pewnym sensie łączę się w bólu
b) jeśli Ci nie przewija−> Twoja przeglądarka jest do niczego.
A w ogóle, wyczyść cookiesy to może przyspieszy.
Poza tym−czemu wszyscy chcą zamknąć ten wątek? Tylko ja go tak lubię, czy co?
31 gru 00:48
Jordan: Może doszli do wniosku że jesteś już wystarczająco udręczona
31 gru 00:50
Basiek: Bzdury.
Potrzebuję do maja ciągłego nękania matematyką, żeby coś z tego było
31 gru 00:51
rumpek: Oooo za pamięci
Basiek z tego co pamiętam to lubisz polski
więc mam takie pytanie: kojarzysz może jakieś dzieło związane z oświeceniem, gdzie ukazany jest
Bóg negatywnie?
bo tylko tego brakuje w mojej bibliografii
31 gru 00:52
Basiek: Rumpek no cześć
To w oświeceniu chyba trzeba szukać czegoś o Bogu Wielki, aczkolwiek
obcym, nie interesującym się człowiekiem i jego życiem. Takie coś znajdziesz, czy to odpowiada
Twojej wizji Boga zlego?
31 gru 00:56
rumpek: nio właśnie w oświeceniu powstały te wątpliwości, różne prądy literackie, tam te nowe
"twierdzenia" deizm itp. gdzie wiara brana jest pod znak zapytania dlatego poszukuje czegoś w
tym.
Ale zastanawiałem się też nad trenami Kochanowskiego (które przepełnione są żalem) ale nic
ciekawego nie znalazłem.
Odpowiadając na Twoje pytanie: co odpowiada wizji Boga złego − to to jak np.: ludzie nie
pokładają ufności w Nim, ukazywany w złym świetle, bardziej martwią się o sprawy ziemskie niż
o duchowe
Ogólnie jakbyś zapodała jakiś fajny utwór gdzie coś takiego jest mam do wyboru: "renesans,
barok, oświecenie"
31 gru 01:00
Basiek: Mnie do tego najbardziej by pasowało "Dies irae" Kasprowicza , coś z Leśmiana lub Gombrowicza,
niestety− to nie te epoki
Ale pogrzebię w jakimś słowniku/ siedzi
jak znajdę coś, dam
znać na pewno.
31 gru 01:03
kylo1303: a motyw buntu przeciw Bogu?
31 gru 01:04
Basiek: Kylo tu masz Leśmiana, Biblia− Adam i Ewa, jako archetyp i coś na pewno się jeszcze
znajdzie
31 gru 01:05
Jordan: Jeżeli mogę wtrącić swoje 23 słowa. Moim zdaniem szkoda tracić czas na pisanie wypracowania
lepiej sobie kupić, a ten czas przeznaczyć na napisanie matury z matematyki na 100%
31 gru 01:06
rumpek: kylo1303 taki temat maturalny
?
31 gru 01:06
Basiek: O, a Konrad w III cz. "Dziadów"− Wielka Improwizacja?
No i "Dies irae" − wyraźna krytyka Boga− surowego władcy.
31 gru 01:07
kylo1303: Ale ja nie pytam o siebie, tylko czy ten motyw nie pokrywa sie z jego tematem. A jesli chodzi o
ksiazki to chyba bardziej Dziady
Ja prace wezme po bracie, nie bede sie meczyl, a z
polskiego to nie przeczytalem ani jednej lektury w liceum i totalnie nic nie robie, to bedzie
jedyna matura "aby zdac"
31 gru 01:07
rumpek: Jordan wolę poświęcić 2−3 dni na napisanie i mieć z głowy, i zdać ustną (bo będę wiedział
co pisze i to zapamiętam) niż dać komuś do napisania i uczyć się tego i wysokie
prawdopodobieństwo, ze się nie zda
31 gru 01:07
kylo1303: A moj temat to "motyw buntu przeciw Bogu"
31 gru 01:08
Basiek: Jordan wtrącić możesz
Hm, ale wiesz, jak to napiszę, to będę umieć, a jak ktoś... to
będę musiała wkuć, to po pierwsze. Po drugie− wolę sobie kupić nową kieckę niż pracę
maturalną. Po trzecie− 1/2 dni poświęcę góra, w tym czasie z matmy nie nauczyłabym się zbyt
wiele
31 gru 01:08
rumpek: No ja tylko przeczytałem z lektur tylko "Pana Tadeusza, Zbrodnie i karę"
"Das ist alles"
no szkoda, że "Dziady" nie ta epoka, Kasprowicz − Młoda Polska
31 gru 01:09
rumpek: no to
Basiek zdanie ma podobne jak ja w tej kwestii
Jednakże ja zamiast kiecki jakieś
kupiłbym zbiór zadań z matmy
31 gru 01:10
Basiek: Ostatnio byłam w większej księgarni, to jak na złość nie mieli zbiorów Kiełbasy!
31 gru 01:13
rumpek: zbiór kiełbasy jest dobry na dwa lata przed maturką, teraz według mnie trochę strata czasu
bo większości takich zadań nie będzie
lepiej kupić Aksjomat lub OE Pazdro
(ja zamawiałem zbiór kiełbasy dwa lata temu za 19zł jeden na gandalfie bodajże
)
31 gru 01:14
kylo1303: Zeby tak nie zejsc z glownego tematu to zadanko:
Uzasadnij ze nierownosc jest prawdziwa (a,b∊R)
a2 + b2+4 ≥2(a+b−ab)
31 gru 01:15
Jordan: Jak w takim ekspresowym tempie jesteście w stanie napisać to bez dwóch zdań
Mi pewnie by to
zajęło ponad miesiąc
Po za tym pracy wcale nie kułem napamięć bo to by się mijało z celem
zapomnę jednego słowa albo nie w tym miejscu postawie przecinek i komisja będzie na nie
31 gru 01:15
Basiek: Ustny polski to jedyne czego się nie boję, chociaż nie mam napisane ani jednej linijki pracy,
ani wybranych książek <3
31 gru 01:16
rumpek: ja tam boje się polskiego i ustnego angielskiego (że pod wpływem stresu pozapominam to co
umiem )
31 gru 01:19
Basiek: Z angielskiego nie mam się czego bać, bo jeszcze nic nie umiem hahaha
Rumpek− a patrzyłeś na poetów przeklętych? W większości ich bunt przeciwko światu,
konwenansom i całej epoce, wiązał się z buntem przeciwko Bogu−> gdzieś go musieli poobrażać
chyba, prawda?
31 gru 01:21
Godzio:
kylo ka bym dał
>
x
2 + 3 > 0
31 gru 01:31
kylo1303: Nie bardzo rozumiem z czym to jest zwiazane
31 gru 01:35
Godzio:
Jak się rozwiąże zadanie to będzie wiadomo
31 gru 01:36
kylo1303: aaa, chodzi ci ze moze byc bez " ...lub rowne" . Ja to zadnie rozwiazalem, ale uznalem ze jest
w miare ciekawe i dam tutejszym maturzystom (zadanie z aksjonamtu wiec niektorzy pewnie juz
robili)
31 gru 01:38
31 gru 01:40
kylo1303: 1. nie mialem analizy matematycznej
2. nie znam zaleznosci miedzy srednimi (jesli mozna to szybko ogarnac to sie wezme, jesli nie
to nie bede nawet zaczynal)
31 gru 01:43
Godzio:
Nie ma co ogarniać
Tu akurat analiza nie ma nic do rzeczy, po prostu przykłady
| a + b | | 2 | |
| ≥ √ab ≥ |
| więcej nie potrzeba |
| 2 | | | |
I to działa na ogólnym przykładzie
| a1 + ... + an | | n | |
| ≥ n√a1...an ≥ |
| |
| n | | | |
Przykład a)
Po przemnożeniu nierówności i pozbyciu się ułamka dostajemy tezę
31 gru 01:45
Basiek: Tutejsi maturzyści czują się dobici ilością zadań, także ilością zadań, których nie potrafią.
Idę spać, jutro muszę dotrwać do północy
Rumpek : mam do Ciebie całą litanię. Po pierwsze− Kochanowski: Tren XI (wszystkie pasują
od IX−XI), w ogóle− patrz tu:
http://chomikuj.pl/basienka_87/ebooki/Anonim/S*c5*82ownik+motyw*c3*b3w+literackich Ten słownik motywów literackich jest najlepszym jaki
widziałam na oczy. Patrz pod "raj, bunt, diabeł, ...) coś się znajdzie
Trzymam kciuki, bo
mam podobny problem z pracą maturalną, jak Ty.
Koniec mojego offtopowania na dziś
Dobranoc i wszystkim szampańskiego sylwestra, jakbyśmy się mieli... nie spotkać
31 gru 01:49
kylo1303: Jeszcze mam takie pytanie odnosnie indukcji, bo mialem to juz dawno:
przypuscmy ze mam udowodnic ze n+2n jest podzielne przez 3
n+2n=3a
1. n=1
2. zakladam ze dla k≥1 jest prawdziwe (k+2k=3a)
3. sprawdzam dla k+1
bla bla bla= 3(a+2)= 3b
Chodzi mi tylko o wytluszczony fragment, czyli oznaczenie a i b. W tezie uzylem "a", okreslilem
ze jest to liczba calkowita itd. Czy moge uzyc ze n+2n=3a oraz k+2k=3a (ta sama litera)? Czy
jak "b" dam na koncu (dodam ze nalezy do C) to bedzie okej? CHodzi mi czy musze wczesniej cos
do tego dodac (jakis komentarz czy cos). Srednio wiem jak opisac to czego nie jestem pewien,
ale jesli to co napisalem jest dobrze (z punkt technicznego) to mi wystarczy.
31 gru 01:49
Godzio:
Uczono mnie, że raczej nie wprowadza się dodatkowej zmiennej "k", więc nie ma problemu z
oznaczeniami
1o n = 1 − ok
2o n + 2n = 3a implikuje (n + 1) + 2(n + 1) = 3b
L = blabla = 3(a + 2) = 3b − to jest ok
I na końcu komentarz z 1o, 2o i ZIM liczba ... jest podzielna przez 3 dla każdego n ∊ N
31 gru 01:56
kylo1303: czyli to by bylo tak jakby tylko na 2 kroki indukcyjne a nie 3. Ja to chyba mialem w pierwszej
klasie, a od tamtego czasu nie korzystalem i tak teraz przy powtorkach w glowie musialem
wynalezc.
P.S. co znaczy "ZIM liczba" ?
31 gru 02:00
Godzio: ZIM = zasada indukcji matematycznej
liczba n + 2n
31 gru 02:02
kylo1303: heh, dzieki. Probuje cos ten przyklad "b", ale jako ze pierwszy raz w zyciu cos takiego robie
to moze mi troche zejsc
31 gru 02:03
kylo1303: dobra, poddaj sie. Nawet nie sadze zebym byl blisko rozwiazania. Chcesz to daj ewentualnei
podpowiedz. Probowalem przeksztalcac pierwsza i trzecia czesc tych zaleznosci (pomijajac ta z
pierwiastkiem) ale cos nie wychodzi
31 gru 02:16
Godzio:
Skorzystaj z arytmetyczna ≥ geometryczna
31 gru 02:17
kylo1303: czyli korzystanie z harmonicznej jest niepotrzebne
no to zaraz bedzie drugie podejscie
31 gru 02:24
Godzio: Sory nie dam rady już
jak wstanę to sprawdzę to co napisałeś
Dobranoc
31 gru 02:29
kylo1303: no napisz odpowiedz
bo nei sadze zebym rozwiazal, ciagle czegos brakuje
31 gru 02:31
Godzio: Weź mi napisz przykład bo nie wiem o który chodzi
2 sty 00:27
Basiek: Mój kącik <3
Ładnie z Waszej strony
2 sty 00:29
2 sty 00:33
kylo1303: przyklad b.
(sry ze z opoznieniem, ale szukalem czy nie ma jakiegos latwego sposobu na znalezienie
pierwiastkow rownania trzeciego stopnia)
2 sty 00:35
Godzio:
| x1 | | x2 | |
| + |
| + ... + xnx1 | | x2 | | x3 | |
| |
| ≥ |
| n | |
| | x1 | | x2 | | xn | |
n√ |
| * |
| * ... * |
| ( wszystko pod pierwiastkiem) |
| | x2 | | x3 | | x1 | |
Widać że to co pod pierwiastkiem się skróci do 1, mnożąc obustronnie przez n otrzymujemy tezę,
początkowa zależność to właśnie arytmetyczna ≥ geometryczna
2 sty 00:38
Benek: Witam.
Czy mógłby mi ktoś wytłumaczyć jak się robi takiego typu zadanie? :
Znajdź rozkład wielomianu na czynniki: w(z)= z4 + 4z3 + 9z2 + 16z + 20, wiedząc, że liczba
zespolona z1=2i jest miejscem zerowym tego wielomianu.
Z góry dziękuję za każdą pomoc
Pozdrawiam.
2 sty 00:39
kylo1303: zaraz przeanalizuje xD (dzieki)
2 sty 00:40
kylo1303: No coz, tak jak mowiles
Godzio banal... nie wiem dlaczego ale w moim umysle zakodowalo sie
ze x
1, x
2,...x
n to jakis ciag, a nie liczby, ktore mozemy podstawic do wzorow (w pewnym
momencie nawet przyjalem ze to ciag arytmetyczny
)
2 sty 00:52
Godzio:
Początki z zadaniami których się nie znało zawsze są trudne
2 sty 00:53
Pepsi2092: Siema wszystkim
Jak macie jakąś nierówność dla mnie żeby wykazać taką na poziom rozszerzony (
nie "banał" od
Godzia która dla niego może jest banałem ale nam głowy urywa ) to poproszę
2 sty 02:17
Godzio:
Udowodnij nierówność
a * b * c * d < n gdzie a,b,c,d są cyframi liczby czterocyfrowej n
2 sty 02:32
Basiek: Przyszłam się pochwalić, że ktoś mi nagadał przez święta tu, że ratuje mnie tylko zbiór
Aksjomatu i pognałam dziś do księgarni
Zakupiłam. Będziemy sobie od dziś razem rozwiązywać
2 sty 15:35
ZKS:
Kto taki Ci nagadał żebyś kupowała trzeba było ściągnąć?
2 sty 15:45
Basiek: ZKS tak, cześć
Po primo− skąd? Po secundo, czy jakoś tak− nie widziałam tego w
internecie? Po trzecie− hm, wyglądam wiarygodniej siedząc nad książką niż przed laptopem,
kiedy udaję, ze coś robię.
2 sty 15:46
ZKS:
Witam
Basiek!
1
o Z internetu
2
o Google
3
o Masz absolutną rację.
Kto Ci
powiedział o tym że Aksjomat jest najbardziej odpowiedni?
I jaki kupiłaś czerwony czy
czarny?
2 sty 15:50
Basiek: Pkt. 1 i 2.−> nie wygooglowałam. Pech
3−> wiem
Nie pamiętam, kto mi to powiedział. Ostatnio niewiele pamiętam...
Czerwony.
Fajnie, kojarzy mi się z krwią, pożogą, ogniem i nieszczęściem− czyli jesteśmy w
temacie.
2 sty 15:52
ZKS:
To mogę powiedzieć że dobrze że tej osoby się posłuchałaś.
Czerwony dlatego bo jak się robi
zadanie to aż krew człowieka zalewa.
2 sty 15:58
Basiek: Osz Ty, potrafisz człowieka pocieszyć
2 sty 16:01
ZKS:
Ale zobaczysz w maju jak to zaowocuje.
2 sty 16:17
Basiek: Bólem głowy?
ZKS− a może by tak jakiś logarytm malutki?
2 sty 16:17
ZKS:
Bólem głowy nie wiem ale wiem na pewno że co najmniej 80% z rozszerzonej matury z matematyki
jeżeli oczywiście będziesz rozwiązywać dużo zadań.
Mam Ci podać jakieś zadnie z logarytmów?
2 sty 16:23
Basiek: Nie, mam własne
log2+log(4
x−2 +9)≤ 1+log(2
x−2 +1)
Najpierw pomnożyć te logarytmy, czy może wstawić jakieś t?
To było tak dawno, jak
ostatnio coś takiego robiłam
2 sty 16:26
ZKS:
Jeżeli chcesz mieć ułatwienie to możesz podstawić 2
x − 2 = t > 0
log
2 + log(t
2 + 9) ≤ 1 + log(t + 1) i teraz możesz sobie po wymnażać na spokojnie.
2 sty 16:28
ZKS:
Ech log
2 a nie log
2 źle napisałem.
2 sty 16:29
Basiek: Bo hm, nie mogę np. po lewej zrobić tak log(2*(4
x−2 +9)= log8
x−2 +.... prawda?
2 sty 16:30
ZKS:
Nie za bardzo.
2 * 4
x − 2 ≠ 8
x − 2.
2 sty 16:38
Basiek: Tak się tylko upewniam.
Gdybym tego nie umiała rozpisać poprzez zmienną t, to w ogóle by się
chyba nie dało zrobić
Stąd tak kombinuję. A w zasadzie− upewniam się
2 sty 16:39
Basiek: Okej, wyszło mi to zad. z logarytmami
to dalej
2 sty 16:48
Pepsi2092: Kurde
Godzio się chyba wkurzył na mnie
Ale to nie miało być złośliwe tylko wręcz
przeciwnie
Godziu z tymi nierównościami
Także przyjmij to jako żart
Ja dzisiaj
niestety nic z Wami nie rozwiązuję, bo mam dzień z fizyką
Ale w najbliższym czasie będę
musiał zwrócić się do
Basiek i reszty, ale głównie do niej bo ona najbardziej czasowa i
maturzystka tak jak ja o pomoc przy ogarnięciu do perfekcji prawdopodobieństwa i działu z
analityczną, głównie chodzi mi o jednokładność
A powiedzcie mi jeszcze czy w stereometrii
jak miałem normalnie na podstawie u siebie i dosyć solidnie przerobilem, ponadto zdaje mi się
że z planimetrii też w miarę daje radę to będę musiał jeszcze bardzo dużo nadrabiać?
A tak
poza to sorry, bo nawet nie zacząłem od "Cześć"
Więc nadrabiam zaległości i
Witam
wszystkich
2 sty 17:06
ZKS:
Masz jeszcze jakieś
Basiek?
2 sty 17:08
Basiek: Zadań?
No mam kilkadziesiąt do przerobienia jak mam być szczera. I owszem, jestem "czasowa",
bo zamiast coś robić, to się obijam
Cześć Pepsi
Analityczna −> ogarnięta
Także spoko.
stereometria− powinno Ci wystarczyć, dla mnie to niestety czarna magia
A planimetria− to
sobie lepiej poćwiczyć tw. sinusów i cosinusów
Tyle w zasadzie
2 sty 17:12
ZKS:
To jak jakieś będzie ciekawe to możesz wrzucić.
2 sty 17:16
Pepsi2092: Basiek pisząc że jesteś czasowa miałem na myśli że dużo czasu spędzasz na tym forum
A
to forum to jest chyba najlepsza rzecz jaka mogła nas spotkać bo dzięki niemu lepiej
przygotujemy się do matury
Ja w stereometrii to najbardziej boje się tych brył wpisanych w
kule i innych różnych tak na pierwszy rzut oka
Ale jakoś pójdzie mam nadzieję
2 sty 17:17
Basiek: Mam takie zadanko...
| | x2−3x−9 | |
Ze zbioru Z={x∊C: x<5 ⋀log( |
| )≥0} losujemy kolejno bez zwracania dwie liczby a, |
| | x−4 | |
b, które traktujemy jako współrzędne punktu P(a,b). Oblicz prawdop., że punkt P należy do
wykresy funkcji y=Ix−1I.
| | 1 | | 1 | |
No i mnie wyszło P(A)= |
| a ma być P(A)= |
| |
| | 5 | | 4 | |
stąd...
według mnie x∊<−1,0,1,2,3>
Ω− wariacją bez powtórzeń, czyli IΩI=25
no a ten P ={(−1,2)(0,1)(1,0)(2,1)(3,2)} <− 5 możliwości
Widzicie jakiś okrooopny błąd?
Wydaje mi się, że musiałam coś nie tak z tym zbiorem wyliczyć , bo dla 4 elementów już by
wyszło
2 sty 17:18
Basiek: Pepsi moja matura z matmy na pewno będzie dzięki temu prostsza. Ale angielski? − będzie
rzeźnia.
Szukam samomotywacji. Albo w ogóle jakiejkolwiek motywacji
2 sty 17:23
ZKS:
| | x2 − 3x − 9 | |
A jak obliczyłaś log( |
| ) ≥ 0 ? |
| | x − 4 | |
2 sty 17:23
Basiek: hm...
(może źle pamiętałam, ale...) to jako współczynnik b>0, sobie liczyłam z twierdzenia o
signum... wyliczyłam pierwiastki i bla bla blaaa, wyszło mi to, co wyszło?
2 sty 17:24
ZKS:
| | | | | |
Ω = | * | mi się wydaje że tyle wynosi moc Ω. |
| | | |
2 sty 17:29
ZKS:
Pierwsza liczbę wybieramy spośród 5 następnie kolejną spośród 4.
2 sty 17:31
Basiek: Już wiem, co zrobiłam źle
Co prawda dalej nie ogarniam tego, co napisałeś powyżej, ale fakt,
chociażby z reguły mnożenia IΩI=5*4=20
I znalazłam błąd u siebie (jak zawsze− idiotyczny)− napisałam sobie ładnie, że wariacja bez
powtórzeń i w ogóle wszystko, a obok policzyłam wzorem wariacji z powtórzeniami ...
2 sty 17:35
Basiek: Dobra, dzięki
ZKS, jesteś naprawdę niezastąpiony
Idę się edukować (tj. wkuwać)
angielski− jak się nauczę tych 500? 600? słówek, to pewnie znów Was nawiedzę, żeby o coś
zapytać
2 sty 17:57
Godzio: Macie zrobić zadanie ode mnie
2 sty 18:36
Basiek: Kto?
I eee, te liczby a, b, c, d są
kolejnymi cyframi tego n?
I
Godzio? Nie gorączkuj się tak.
2 sty 18:41
2 sty 19:20
Krzyś: ja mam dla ciebie zadanko
1.Wykaż, że dany ciąg an= 3n/14, gdzie n∊N+ jest ciągiem geometrycznym
2 sty 19:24
ZKS:
Macie zrobić zadnie które podał
Godzio.
2 sty 20:21
Basiek: Faceci....
Ja zadałam powyżej konstruktywne pytanie i proszę o odpowiedź
W innym wypadku nawet tego na
kartkę nie przepisuję
2 sty 20:30
ZKS:
Kobieta ...
To przyjmij sobie że są kolejnymi cyframi.
2 sty 20:39
Basiek: To może potem?
Może jednak poczekam na odp. samego Godzia. Ale najlepiej, żeby nie
odpowiadał tak od razu.
Mam jeszcze duuużo nauki.
2 sty 20:41
ZKS:
Nie ma potem jest tylko teraz.
To ja Ci napiszę to są kolejne cyfry tego n lepiej?
2 sty 20:44
Basiek: A, jeśli mi tak powiesz, to ja Ci odpowiem, że będę mieć czas w środę po południu.
2 sty 20:47
ZKS:
Ojj tam
Basiek zrób teraz.
Dostaniesz
.
2 sty 20:51
Basiek: Ostatnio miałam uczulenie na jabłka
Już ich nie jem
2 sty 20:52
ZKS:
To szkoda.
2 sty 20:54
Basiek: Pamiętaj: jabłka są zbyt zdrowe i zbyt dietetyczne.
A tak serio− dziś śpię nad książkami
A na te Godzia tortury nie mam ani sił, ani pomysłu.
Gdzie jest
Kylo?
On uwielbia robić zadania od Godzia!
2 sty 20:56
2 sty 20:58
Basiek: Gdyby chodziło o gary, to bym jeszcze zrozumiała...
ICSP , weź, pomóż koledze, a nie
Na
mnie zwalać
2 sty 21:00
ICSP: Ja już zdałem maturę
Ty musisz ćwiczyć
2 sty 21:00
Basiek: Chyba na wfie...
2 sty 21:01
ZKS:
Wystarczy zapisać tą liczbę n w postaci a , b , c , d.
2 sty 21:06
Basiek: Udowodnij nierówność a * b * c * d < n gdzie a,b,c,d są cyframi liczby czterocyfrowej n
2 sty 21:09
Basiek: Dobra, teraz widzę
Okej, toż wiem, że trzeba rozpisać... po to pytałam o to, czy są
kolejne
abcd<1000a+100b+10c+d
Ale dalej to ja już nie wiem
2 sty 21:10
ZKS:
No to do pracy zadanie jest fajne.
2 sty 21:11
Basiek: Kiedy ja mam zrobić jeszcze 35 zad. na matematykę. + mam 2 spr
I dowiedziałam się, że mam na
jutro przeczytać Przedwiośnie...
A takie myślenie, to pracochłonne jest
2 sty 21:13
ZKS:
Podziel obustronnie przez abcd i wyciągnij wnioski.
2 sty 21:15
Basiek: Mnożyłam, dzieliłam.., ale hm
Da się w ogóle coś takiego wywnioskować z tej postaci?
2 sty 21:18
ZKS:
Rozdziel lewą stronę na 4 ułamki wtedy na pewno coś wywnioskujesz.
2 sty 21:21
Godzio:
Byłem na uczelni i tylko wszedłem zobaczyć czy ktoś zrobił zadanie ode mnie
Co do zadania, chyba nawet nie trzeba dzielić
2 sty 21:21
ZKS:
Oczywiście że nie trzeba ale to już trzeba być naprawdę spostrzegawczym aby od razu zauważyć
więc poradziłem aby podzielić i wyciągać wnioski.
2 sty 21:23
Godzio:
E tam, nie aż tak spostrzegawczym
2 sty 21:24
Basiek: Buuu. Rozumiem. Faktycznie się zgadza. Gdybym nie była sobą, to poszłabym płakać w poduszkę nad
własną głupotą, ale chyba zamiast tego się pośmieję.
2 sty 21:24
Basiek: I no, w zasadzie z tej postaci też można wywnioskować bez dzielenia, bo dla liczb a,b,c,d=9
(wartość max mianownika)
całość jest równa= U{9999/6561} >1 suma... bla bla
cnu. ^^
2 sty 21:26
Godzio:
No to tak elegancko:
abcd ≤ a * 9 * 9 * 9 < 10 * 10 * 10a = 1000a < 1000a + 100b + 10c + d
2 sty 21:28
Basiek: Czy można popaść w kompleksy przez zadanie z matematyki? − Cóż, widać można.
2 sty 21:31
Godzio: | | ab | |
Wykaż, że jeśli a > 2 i b < 4, to |
| + 4 < b + 2a |
| | 2 | |
Myślę, że nie jest z działu super trudne
2 sty 21:39
Basiek: Myślę, że czekamy na
Kylo
2 sty 21:40
Godzio:
Rób, nie ma co
mam jeszcze parę zadanek
2 sty 21:40
Godzio:
Ale wiesz co, jeszcze nie wiesz co to są trudne zadania
Miałem już 2 zadania takie na prawdę
trudne, jedno zajęło mi 1,5 A4, a drugie 4 A4
czasowo nie mówię bo się załamiesz
2 sty 21:42
Basiek: Ja też, dokładnie 37.
A moja paaani od matematyki nie jest tak miła jak Ty, więc wolę zrobić
te jej
2 sty 21:42
ZKS:
Godzio fajne zadnie.
Basiek spróbuj zrobić.
2 sty 21:57
Eta:
2 sty 21:59
Basiek: ZKS Ciebie też się nie boję
2 sty 22:02
ZKS:
Bo Cie za szantażuje i nie pójdę na Twój ślub.
2 sty 22:04
Basiek: Ojej, no weź, mocny argument. Przemyślę to. Mogę wysłać odpowiedź pocztą?
2 sty 22:06
ZKS:
Wolę tutaj rozwiązanie ale zaproszenie możesz wysłać pocztą.
2 sty 22:11
Basiek: Mówił Wam już ktoś, że jesteście niemożliwi?
Nie?
2 sty 22:12
ZKS:
Hmmm musiałbym się zastanowić.
2 sty 22:14
ZKS:
Tytuł postu w końcu musi być adekwatny prawda.
2 sty 22:17
kylo1303: Witam. Nie chce mi sie czytac wszystkiego wiec mozecie dac ponownie (albo podac godzine) to
moge cos poprobowac
2 sty 22:19
ZKS:
Oczywiście tematu nie postu hehe.
Dobra idę jeszcze się pouczyć na jutro niestety. Miłego
wieczoru życzę aby dobrze się zadanka rozwiązywało.
2 sty 22:19
Basiek: Dzięęęki, wzajemnie.
Dobranoc.
2 sty 22:21
Basiek: 21:39, Kylo
2 sty 22:21
kylo1303: ab+8<2b+4a
ab−4a − 2b+8<0
a (b−4) − 2(b−4)<0
(b−4)(a−2)<0 i a > 2 i b < 4
a−2>0
b−4<0
+ * − daje minus
2 sty 22:22
Godzio:
Ok
2 sty 22:26
Godzio:
W trójkącie ABC długości boków wynoszą:
|AB| = c, |AC| = b, |BC| = a, gdzie 0 < a < b < c.
Pole tego trójkąta wynosi 3. Wykaż, że |AC| > √6.
2 sty 22:27
kylo1303: Apropo tego zadania abcd>n, to czy moznaby zrobic cos na takiej zasadzie:
Maksymalny iloczyn =94=6561, wiec a≤6, a wtedy maksymalny iloczyn wynosilby juz 6*93=4374 itd
(az dojdziemy do jedynki i wyjdzie ze iloczyn nie moze byc wiekszy). Wiem ze to myslenie ma
jedna luke, nie zwracam uwagi na b,c,d (przyjmuje ze sa to 9tki a oczywiscie tez sa
ograniczenia, ale stosuje zasade ze jesli wieksza liczba jest mniejsza to i mniejsza tez
bedzie mniejsza− to sie chyba nazywa po lacinie "a maiori ad minus" ale nie wiem czy dobrze
uzylem tej "sentencji")
2 sty 22:34
kylo1303: Jeszcze jedno, zanim zaczna robic zadanie, czym sie rozni Aksjomat czarny od czerwonego?
2 sty 22:37
Godzio:
No tak, ale to chyba się sprawdzi jeśli sprawdzisz wszystkie przypadki, po za tym ja w
rozwiązaniu wykorzystałem to maksymalne ograniczenie, więc raczej nie ma sensu bawić się w
mnożenie itd.
2 sty 22:38
kylo1303: Tzn wiem ze twoje rozwiazanie jest duzo lepsze, ale tak z ciekawosci spytalem. Teraz musze
poszukac wszystkich wzorow na pole trojkata bo pamiec juz zawodzi
2 sty 22:40
Eta:
Widzę moje zadanie
bla bla .. |AC| >
√6
2 sty 22:42
Godzio:
@
Eta zdaje się, że kiedyś nie umiałem go zrobić
| | ah | |
kylo wydaje mi się, że starczy wzór P = |
| |
| | 2 | |
2 sty 22:48
Eta:
2 sty 22:49
Eta:
Dobiłam Wam post nr
700 
Poczekam na
1000
2 sty 22:51
kylo1303: | | 1 | |
w zasadzie to chcialem znalezc (sprawdzic czy sie nie myle) wzor P= |
| ab*sinα. Jak na razie |
| | 2 | |
mam jedna koncepcje ale wydaje mi sie ze zbyt skomplikowana, musialbym zamieniac sinusy na
cosinusy i potem z twierdzenia cosinusow cos probowac, a zapewne wyjdzie z tego przyslowiowa
kupa.
2 sty 22:52
kylo1303: Jak zwykle wszystkie laury wedruja do
Eta. Gratulacje
2 sty 22:53
Eta:
kylo ......... główkuj bez sinusów
2 sty 22:57
Vax: Idzie bardzo szybko z sinusów
2 sty 22:58
Eta:
Bez ......... też
2 sty 22:59
kylo1303: aha, czyli utwierdzacie mnie w przekonaniu ze z planimetrii kuleje
zaraz moze cos zauwaze,
pokombinuje z wysokosciami (moj najgorszy dzial
)
2 sty 23:00
kylo1303: Zrobilem (jupii). Po wykonaniu 6 rysunku wpadlem na to zeby wysokosc poprowadzic z B a
nie z C (tak bylo fajniej rysowac) i dalej jakos poszlo.
2 sty 23:13
2 sty 23:15
Eta:
2 sty 23:15
kylo1303: No to twoje rozwiazanie to wiem, ale tak rozkminialem ten sposob Beztroskiego, w sumie nie
wiem jak skomplikowane byly te jego przeksztalcenia.
2 sty 23:23
3 sty 16:18
kylo1303: Dobra, odswieze stary temat swoimi pytankami:
Napisz rownanie kwadratowe postaci x
2+bx+c=0 ktore ma dwa rozne pierwiastki x
1,x
2, takie ze
ich iloczyn jest rowny 6 oraz bla bla bla
W rozwiazaniu zadania to problemow nie ma, chodzi mi bardziej o kwestie zapisu, a dokladnie o
delte. Jest powiedziane ze maja byc 2 pierw. , wiec Δ>0. Pytanie brzmi czy moge zalozyc ze
jest wieksza, znalezc dane wspolczynniki i potem najwyzej sprawdzic? Czy raczej musze na
wstepie cos orkeslac, pisac zaleznosci b od c itd
I drugie, tu tez pytanie typu "czy tak moze byc":
Mam wykazac ze rownanie nie ma rozwiazan calkowitych:
Doprowadzam do postaci:
| | W(x) | |
I teraz okreslam sobie to jako |
| . Zeby wyszla liczba calkowita to wielomian W(x) |
| | P(x) | |
musi sie dzielic przez P(x), wiec W(−1)=0, sprawdzam licznik i wyjdzie ze W(−1)=−1 . Czy to
juz jest udowodnione (sadze ze tak)?
Inna forma zapisu moze byc: x(x−
√2)(x+
√2)=−(x+1)
4 sty 19:03
Basiek: Hej
Kylo, wtrącę się, bo lubię
Przy takich założeniach, ze masz tylko to podane w zadaniu, to najlepiej pewnie napisać
Δ=b
2−4c i Δ≥0 ⇒ b
2−4c≥0, b
2≥4c .Jest masa takich czepialskich
a nigdy nie wiadomo, kto
się trafi, a to tylko minuta roboty
A na koniec rozwiązania i tak musisz sprawdzić z tym
założeniem. Tak powinno być chyba optymalnie.
4 sty 19:15
kylo1303: Ogolnie to tak tez zrobilem, pytalem z czystej ciekawosci. Wazniejsze jest to drugie, bo tutaj
to juz kwestia czy zadanie jest skonczone czy nie.
4 sty 20:47
Basiek: Jeśli powołasz się na twierdzenie Bezout, to nie masz innej opcji
Zostało udowodnione
Ale zostałabym przy tym twierdzeniu, bo chyba zapis późniejszy niewiele wnosi do sprawy
4 sty 20:49
ZKS:
Piszesz że Δ > 0 ⇒ b2 − 4c > 0 ⇒ b2 > 4c ponieważ trzeba założyć że ma dwa różne pierwiastki
i musi być spełniony taki warunek. Później kiedy rozwiążesz sprawdzasz czy wyniki spełniają
założenie.
Co do drugiego pytania zakładamy że x ≠ −1 i możemy teraz pomnożyć obydwie strony przez x + 1
dostajemy:
x3 + 1 = x ⇒ x3 − x + 1 = 0 I aby to równanie miało pierwiastki całkowite dzielniki wyrazu
wolnego muszą wyzerować ten wielomian (twierdzenie Bezouta) jedynymi dzielnikami wyrazu
wolnego jest ±1 więc sprawdzamy tylko W(1) ponieważ D = ℛ \ {−1} okazuje się że nasz
wielomian się nie zeruje więc wielomian nie posiada pierwiastków całkowitych.
4 sty 20:50
Basiek: ZKS wypowiada się jako autorytet od spraw wykazywania.
4 sty 20:52
Godzio:
Ale po co tak kombinować
?
x ≠ − 1
(x
2 − x + 1)(x + 1) = x [zauważamy wzór skróconego mnożenia]
x
3 + 1 = x
x
3 − x + 1 = 0
Z tw. o pierwiastkach wymiernych mamy, że jedynymi kandydatami na pierwiastki wymierne jest 1 i
−1, z tym, że −1 nie należy do D więc sprawdzamy tylko 1:
W(x) = x
3 − x − 1
W(1) = 1 − 1 + 1 = 1 ≠ 0, zatem równanie nie ma rozwiązań całkowitych, ba wymiernych nawet
4 sty 20:53
Godzio:
No spóźniłem się
4 sty 20:53
Basiek: Następny...
Może wymyślicie jeszcze jakichś kilka możliwości?
To może być ciekawa zabawa.
4 sty 20:54
ZKS:
Chyba pierwszy raz jestem pierwszy od
Godzia.
4 sty 20:55
McJntoshka: Witam, przepraszam ze tu pisze (w nieodpowiednim miejscu) ale jak mam sie zarejestrowac i dodac
nowe zadanko do rozwiazania ? Dziekuje z gory.
4 sty 20:58
Godzio:
Basiek a co Ty na to na takie rozwiązanie:
| | x | |
Całkowite rozwiązania mogą istnieć tylko wtedy gdy |
| jest liczbą całkowitą, |
| | x − 1 | |
(dlaczego? ano dlatego, że dla całkowitych x lewa jest zawsze całkowita, zatem prawa też musi)
| x | | x − 1 | | 1 | | 1 | |
| = |
| + |
| = 1 + |
| Jest to liczba całkowita tylko |
| x − 1 | | x − 1 | | x − 1 | | x − 1 | |
dla x = 0, sprawdzamy czy równość zachodzi:
x = 0
L = 1, P = 1 − 1 = 0
Nie zachodzi, więc nie ma rozwiązań całkowitych
hmm
?
4 sty 20:59
Basiek: Na tym głównym panelu forum, masz fioletowy napisz "Dodaj nowe zadanie"
4 sty 20:59
Godzio:
@McJntoshka
Kliknij w "dodaj nowe zadanie" na głównej stronie
4 sty 21:00
ZKS:
Basiek hmm słyszałem że dzisiaj robisz zadania z Aksjomatu to prawda?
4 sty 21:00
Basiek: Godzio, że brzmi mądrze.
(Cyferki opuściłam wzrokiem). Wiesz, przyjmuję za prawdziwe
wszystkie Twoje rozwiązania, chyba niebezpodstawnie.
4 sty 21:00
Basiek: ZKS Basiek hmm słyszałem że dzisiaj robisz zadania z Aksjomatu to prawda? sens logiczny:
0.
Idę spać
4 sty 21:01
Godzio:
To może zadanie od Godzia
?
4 sty 21:02
edeas: Hm jak ustalic liczbe rozwiazan dla rownania
cosx=x2+1
4 sty 21:04
Godzio:
Basiek wybieraj:
Zestaw: 1 lub 2
Zadanie: Od do 6
4 sty 21:05
Godzio: Od 1 do 6 *
4 sty 21:05
Godzio: @
edeas załóż swój temat a ktoś pomoże, nie wykluczam, że nawet ja
4 sty 21:05
McJntoshka: Godzio, dziekuje, wczesniej tego tam nie bylo i nie wiem jakim cudem ")
4 sty 21:06
4 sty 21:06
kylo1303: Jesli chodzi o Aksjomat to jestem w trakcie przerabiania (dzisiaj chyba ukonczylem 8 test, w
kadzym badz razei przede mna fukncje). A zadanie mozesz dac, i tak sie nudze a nie chce mi sie
robic juz z ksiazki.
4 sty 21:08
Godzio:
To wybieraj [P[kylo] zestaw i zadanie
4 sty 21:10
kylo1303: I dzieki za zadanko, do tego akurat doszedlem ze dzielic sie moze tylko przez 1 i −1 i takie
tam, ale nie wiem gdzie mi 1 uciekla. Zadankoa to najlepiej z "wyrazen algebraicznych", ale
moze byc inne.
4 sty 21:10
kylo1303: Zestaw 1 zadanie 4
4 sty 21:10
Basiek: A ja idę spać
W ciągu ostatnich dwóch dni łącznie ok. 6h. Poruszam kończynami jedynie dzięki
kawie.
Dobranoc
4 sty 21:11
Godzio:
Proste wybrałeś
Rozwiązać równanie
No ale zobaczymy czy poprawnie wszystko obliczysz
Takie typowo maturalne
4 sty 21:13
kylo1303: Czy wynik to:
| | π | | 5π | |
x= |
| +2kπ v x= |
| +2kπ , k∊C |
| | 6 | | 6 | |
4 sty 21:25
kylo1303: Jak cos to moge podac rozwiazanie, dziedzina to x≠kπ gdzie k∊C.
4 sty 21:26
Święty: Zrobiliście ludziom taką chętkę tym Aksjomatem, że sam postanowiłem zajrzeć do tej czerwonej
książeczki
4 sty 21:29
Godzio:
Zadanie zrobione ok, wybieraj dalej (proponuję zestaw 2)
1 − podstawa
2 − rozszerzenie
4 sty 21:30
kylo1303: Zestaw 2 (niech juz ci bedzie) i zadanie 3
4 sty 21:31
kylo1303: (i juz nie bedzie kolorowych napisow bo pewnie z zadaniami kolorowo tez nie bedzie xD)
Leca jeszcze nastepne pytania: Czym sie rozni Aksjomat czarny od czerwonego (ja mam kserowany
wiec nie mam pojecia nawet ktora to czesc− wiem ze dla rozszerzenia).
I drugie (to do studentow bardziej): czy jest jakis dzial/temat/wzory wykraczajace poza
material liceum, ale ktore spokojnie da sie samemu opanowac oraz ktore moga sie przydac w
zadaniach maturalnych. Chodzi mi o to ze czasem dobrze miec alternatywny sposob rozwiazania.
4 sty 21:33
Godzio: Trójkąt równoboczny ABC o boku a wpisano w okrąg. Na łuku BC wybrano punkt
D tak, że proste AB i CD przecinają się w punkcie E i |BE| = 2a. Obliczyć pole S
| | 1 | |
czworokąta ABCD i wykazać, że S = |
| (|BD| + |CD|)2√3 |
| | 4 | |
4 sty 21:37
kylo1303: Tylko nie to... powiem szczerze ze nie mam ochoty na planimetrie
No ale zaraz zobacze
co da sie zrobic
4 sty 21:42
Godzio:
Dodam, bardzo ambitne zadanie
4 sty 21:48
kylo1303: Domyslam sie... jak na razie sporzadzilem odreczny rysunek bo nie chcialo mi sie wstawac po
cyrkiel czy linijke, ale wyszlo znosnie, da sie co nieco rozczytac xD
4 sty 21:50
kylo1303: Mam tylko takie pytanie bo sam sie zaczynam gubic: Czy DB=CD=r ? (tak by mi wychodzilo ale
jakos tak nie do konca jestem przekonany, a nie chce brnac dalej)
4 sty 22:07
Godzio:
No ja też nie jestem przekonany, jak mi to pokażesz, że tak jest to uwierzę
4 sty 22:09
kylo1303:
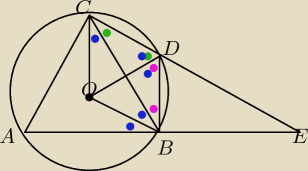
kropka niebieska=30
0
kropka zielona= α
kropka fioletowa=β
trojkat CDO jest (conajmniej) rownoramienny, ramiona to promienie. Kąt C jes trowny 30+α wiec i
kat D to 30+α (u mnie zielona + niebieska). Tak samo robie z trojaktem OBD tyle ze wstawiam
tam β.
W trojkacie BCD:
Laczna suma katow to 60 (2 niebieskie) +2*(α+β)180 czyli (α+β)=60. Dzieki temu wiem ze kąt
D=120. Kat BOD=2α (bo 2 pozostale katy to 30+β).
Dodatkowo wiem ze kat E=β, kat EBD=α+60 i kat BDE=60
Zaraz bede kontynuowal, ale cos mi ucieklo juz z glowy bo z tego nei wynika ze sa rowne te boki
co podalem. Ale widocznie sa xD
4 sty 22:27
kylo1303: Po 10min symulacji doszedlem do wniosku ze jednak CD nie rowna sie BD i to nei jest promien
Teraz moge kontynuowac zadanie z czystym sumieniem (rysunek mam strasznie mylacy).
Tylko zeby sie nie okazalo ze tak jest naprawde
4 sty 22:39
Basiek: Wiecie co?
Nie mogę spać.
Wezmę jedno zadanko, ale tak z funkcji, analitycznej lub ew. coś z ciągów, co?
4 sty 22:40
kylo1303: zapraszam do zabawy z tym xD
4 sty 22:46
Basiek: Planimetrię i stereo to ja muszę zacząć od podstawy przerabiać
4 sty 22:48
kylo1303: Robilem wszystkiego aby tego uniknac ale chyba zaczne kombinowac z trygonometria...
4 sty 22:49
kylo1303: W tym rzecz ze ja tez, moj slaby punkt a ty Godzio mnie napastuje "latwymi" zadaniami. To
co dal z podstawy to spokojnie mogloby byc na rozszerzeniu xD
4 sty 22:50
Basiek: "Seeeercem jestem przy Tobieeee"
Powodzenia.
4 sty 22:50
Basiek: No
Godzio albo ktoś.
Ja tu przychodzę normalnie pełna wiary w możliwość zrobienia
jakiegoś zadanka to nikt nie reaguje. A jak nie mam sił, to wszyscy mi podsyłają jakieś
zadania.
4 sty 22:54
kylo1303: To ja ci dam:
Wyznacz wszystkie wart. parametru a dla ktorych nierwonosc:
(a−1)x2−(a+1)x+a+1>0
jest spelniona przez kazda liczbe rzeczywista.
4 sty 22:56
kylo1303: Z zadaniem posunalem sie do przodu, β wyjdzie tak okolo 16 stopni xD Wniosek z tego taki ze nie
ma sensu liczyc katow, wiec zmarnowalem szmat czasu na niepotrzebne rzeczy xD
4 sty 22:58
Basiek: To jest jakieś zad. z Aksjomatu?
Planuję sobie coś z tego odznaczać
4 sty 23:02
kylo1303: Tak, robilem 2 prawie identyczne zadania i to costam mi nei wyszlo, musialem sie gdzies machnac
w obliczeniach wiec daje tobie zeby mi bylo prosciej (tak, wykorzystuje Cie)
na oslode. Jak
zrobisz to powiem z ktorego dzialu/testu/strony zadanie
4 sty 23:05
Basiek: eee, nie wiesz co to znaczy "wykorzystywać"
Ktoś Cię będzie musiał nauczyć
wyszło mi coś hm, dziwnego
Idę o zakład, że źle
4 sty 23:09
Godzio:
Takie warunki muszą zostać spełnione
4 sty 23:15
Godzio:
Basiek z ciągów powiadasz hmmm
4 sty 23:15
Basiek: ej
ej!
EJ. No ukatrupię, właśnie stwierdziłam, że muszę dać założenie do a−1 , odświeżam,a tu
Godzio to napisał. Blech.
Jesteś nie w porę. Gratulacje.
4 sty 23:16
Godzio: Podstawy czterech logarytmów liczby x tworzą˛ ciąg geometryczny o ilorazie x. Wyznacz
pierwszy z tych logarytmów jeśli jest on mniejszy od −1 oraz suma dwóch pierwszych logarytmów
jest równa sumie dwóch pozostałych
4 sty 23:19
Godzio:
4 sty 23:20
kylo1303: | | 10 | |
Wynik wyszedlby ci dobry. Mi wychodzilo |
| , ale to beznadziejnie glupie przeoczenie:
|
| | 3 | |
| | 5 | | 10 | |
Wyliczylem a1=−1 a2= |
| , a na osi zaznaczam |
| ... |
| | 3 | | 3 | |
4 sty 23:25
Basiek: Czekaj!
Jest problem z tym wcześniejszym.
Znajdź błąd, co?
1) a−1>0 => a>1 (to sobie zostawiam w spokoju)
2) Δ<0
(a+1)
2−4(a−1)(a+1)<0
−3a
2+2a+5<0
√Δa= 8
a
1=−1
=>
{a>1
| | 5 | |
ostatecznie: a∊( |
| , + ∞), co nijak ma się do odpowiedzi |
| | 3 | |
No i ten− pytanie z serii "poziom podstawowy" − tam jak mam przed b minus, to jak liczę deltę
to mogę (−b)
2=b
2 i po prostu ten minus pominąć?
4 sty 23:25
Basiek: A jednak, wyszło mi O.o
Aczkolwiek pytanie powyżej dalej aktualne.
4 sty 23:27
Godzio:
A jaka jest niby odpowiedź
?
4 sty 23:28
Godzio:
Możesz pominąć: )
4 sty 23:29
Basiek: Hm, cóż, ja z góry zakładam, że odp. jest zła, więc nie sprawdziłam. Moja wina.
4 sty 23:29
Basiek: W ogóle, ciągi są ok. Ale logarytmów nie znoszę
4 sty 23:32
kylo1303: Odpowiedz jest dobra przeciez.
Godzio − teraz zrobilem sobie przerwe ale zaraz robie drugie podejscie z dorbym rysunkiem
ktory nie bedzie mnie mylil, jesli to nie wypali, a pewnie nie wypali, to dasz
podpowiedz/rozwiazanie zebym mogl spokojnie zasnac. Jestem cienki jak barszcz (czy jak costam)
praktycznie z calej geometrii...
4 sty 23:33
Godzio:
Jasne
robiłem to zadanie kilka dni
4 sty 23:34
Basiek: Kylo nie śpisz przez następnych kilka dni
4 sty 23:36
Godzio:
Nie wiem czy mam gdzieś rozwiązanie, jeśli miałbym się od nowa brać to też myślę, że kilka
dobrych godzin by zajęło
4 sty 23:37
kylo1303: Chyba sobie kpisz....
4 sty 23:39
Basiek: Chciałabym zobaczyć Twoją minę Kylo, może jakaś słit focia, żebym mogła umrzeć
szczęśliwie...
4 sty 23:41
Godzio:
Haha, aż tak przeraziłem
4 sty 23:42
kylo1303: taa... w kazdym badz razie konsekwencje z tego "milego" doswiadczenia sa nastepujace:
1. Jesli
Godzio mowi ze zadanie jest ambitne, to na jezyk polski znaczy:
Trzymaj się od tego z daleka
2. Straciłem jakąś godzinke czy może poltorej, moglbym zrobic z 10 zadan z tego samego dzialu
ale na normalnym poziomie
3. Nie bedzie mnie dreczyla mysl ze nie zrboilem zadania
4 sty 23:46
kylo1303: Wiec mozna by rzec ze jest jeden plus, jeden minus i przestroga, wiec w sumie wychodzi na
+
4 sty 23:47
Basiek: A co do tego mojego śmiesznego logarytmowego
ciąg: a, ax, ax2, ax3
y− nasza logarytmowana liczba
logay≥1 (kompletnie nie wiem, jak zastosować, póki co)
logay+logaxy=logax2y+ logax3y
Powinnam zmienić podstawy logarytmów na jakąś wspólną, tak?
4 sty 23:48
Godzio:
Chodzi o to, żeby siedzieć nad zadaniem, korzystać z różnych metod (przez to lepiej się je
pamięta i wie gdzie można zastosować). Na tym polega robienie trudnych zadań, na pomysł się
chop siup nie wpadnie, pamiętaj ! A to nie była stracona godzina, jeśli miałbyś zrobić jakieś
beznadziejne zadania, które robi się schematycznie, to nie było by dla Ciebie korzyści, a tak
kombinujesz, liczysz, a nóż zauważysz jakąś własność
4 sty 23:48
Godzio:
Przeczytaj dobrze zadanie
4 sty 23:50
kylo1303: Spokojnie, ogolnie to i tak planuje jutro do szkoly wziac moj wypasiony rysunek i tam
poprobowac. Jak to nie wyjdzie to mam inny pomysl: wezme papier milimetrowy, narysuje wszytsko
jak najdokladniej, policze "recznie" katy i dlugosci i posprawdzam. Dzieki temu moze wpadne na
jakies zaleznosci.
P.S. "lepiej sie je pamieta" − powiedziala osoba co nie pamieta zadania xD
4 sty 23:51
Basiek: Mówiłam już, że nigdy nie czytam poleceń?
4 sty 23:51
Godzio:
Zadanie robiłem raz w życiu jakieś półtora roku temu
Ale za to znam wszystkie wzory na pamięć, zależności w figurach geometrycznych, zwłaszcza te
ciekawsze
4 sty 23:53
Godzio: Więc ślęczenie nad ciekawymi zadań to podstawa bardzo dobrze zdanej matury !
4 sty 23:54
Godzio:
Basiek i jak ta z tym "banałem"
4 sty 23:59
Basiek: Ano wiesz... nijak. Poprawiłam dane.
To zawsze coś.
5 sty 00:00
Godzio:
log
ax < − 1
log
ax + log
axx = log
ax2x + log
ax3x
Teraz do wspólnej podstawy (jakiej ?) i dalej już z górki
5 sty 00:04
5 sty 00:05
Trivial:
Osiemsetny post! Dalej, dalej − do tysiąca!
5 sty 00:05
Godzio:
Nie udało się
Trivial spóźniłeś się
5 sty 00:06
Trivial: Te posty nigdy się nie udają.
5 sty 00:07
Trivial: ... I właśnie to w nich najlepsze.
5 sty 00:07
Tragos: wg mnie wynik: logax = 0
5 sty 00:07
kylo1303: Wow, i to mnie kopnal zaszczyt dodania tego jakże zacnego, osiemsetnego postu
Teraz ludzie
beda mnie szanowac, a dzieci opowiadac wnukom!
5 sty 00:08
Godzio:
kylo Prawie dobry wynik
5 sty 00:09
Godzio:
Tragos, założenie jest
log
ax < − 1 więc Twoja odpowiedź nijak się ma do tego
5 sty 00:10
Trivial: A tak właściwie, to co dzieje się w tym wątku, że aż tyle odpowiedzi ma?
5 sty 00:10
kylo1303: Co prawie!? Zapisac w innej formie czy gdzies maly blad?
| | −(6+2√3) | |
logxa= |
| a dalej chyba sie nie pomylilem Przejrze jeszcze raz .
|
| | 4 | |
Chyba ze chodzi o to ze musze dodac
x≠a
5 sty 00:11
Tragos: no właśnie teraz zauważyłem, że jeszcze to jest
hym myślę dalej
5 sty 00:11
Godzio:
Nie wiem
Basiek spamuje
A tak ogólnie to my wsadzamy zadania, a maturzyści je robią
5 sty 00:11
Godzio:
Nie zjadłeś nigdzie ?
5 sty 00:12
Basiek: Ja nie spamuję....
5 sty 00:13
kylo1303: Rownanie kwadratowe wyszlo mi takie:
2t
2+6t+3=0 gdzie t=log
xa
Δ=12 ⇒
√Δ=
√12=2
√3
| | −6−2√3 | |
t1= |
| , t2 nie jest mniejsze od −1 |
| | 4 | |
5 sty 00:15
Basiek: Ych, dlatego mi głupoty wychodzą! Delty nie spierwiastkowałam przy liczeniu −−
5 sty 00:16
Godzio:
No to dobrze Ci wyszło
, widocznie źle policzyłeś liczbę odwrotną
5 sty 00:17
kylo1303: Ale ty masz rozwiazanie w jakiejs ksiazce czy sam liczyles? Bo moze zamiast t1 wziales t2?
Zaraz sprawdze ponownie
5 sty 00:18
Basiek: To mam pytanie, jak już dowlekłam się do logxa, to jak obliczyć logax ?
5 sty 00:19
Godzio:
Ja liczę wszystko w wolframie
Nie chce mi się, a przy tym nie robię błędów
5 sty 00:19
kylo1303: ... a ja licze wszystko recznie, zaraz wrzuce do tego wolframa to sobie sprawdze
5 sty 00:20
5 sty 00:20
Basiek: Dooobra, dotarło, dzięki. Z tego korzystałam przy zamianie podstawy. Cudnie. Idę szukać klamki
5 sty 00:21
kylo1303: no to wolfram mowi to co ja:
| | 1 | | 1 | |
t= |
| (−3−√3) czyli − |
| (3+√3) (potem musze pozbywac sie niewymiernosci i dlatego |
| | 2 | | 2 | |
mnoze przez 3−
√3
5 sty 00:22
Godzio:
Hmmm
w takim razie ok, ja chyba coś źle popatrzyłem, sorki za mieszanie
5 sty 00:23
Trivial:
Czyli
f(x) = 2
√x + c.
5 sty 00:24
Godzio:
Po prostu ?
Tak to zapisałem, ale stwierdziłem, że po pierwsze za proste, po drugie trzeba to jakoś
wykazać
5 sty 00:25
Trivial: Aha.
5 sty 00:27
Basiek: Dobranoc.
Do jutra, tj. dzisiaj
5 sty 00:56
Godzio:
Hehe, dla mnie do jutra
Dzisiaj mamy nockę z analizą ze znajomymi
5 sty 01:11
Basiek: Ma ktoś może czerwony Aksjomat i może mi "zarzucić" jakimś zadaniem?
Coś bym zrobiła, ale
sama wybieram te, które umiem/ nie muszę nad nimi myśleć
5 sty 21:37
5 sty 21:55
Basiek: Ojejjjj
To chyba moje pierwsze jabłko od Ciebie. Cóż, czuję się zaszczycona
, dziękuję
Eta
5 sty 21:57
5 sty 22:04
Basiek: Nie wiem, czy wspominałam, ale mam uczulenia na jabłka.
Teraz zaczęłam się martwić, że to w
ramach pozbycia się mnie, te jabłka
5 sty 22:05
Eta:
Ależ nie! ........to za określenie,że "jestem niedobra"
5 sty 22:07
Basiek: Prawdopodobnie nie doczytałaś ostatniego postu
Udowodniłabym, aczkolwiek wątku znaleźć nie
potrafię
5 sty 22:09
ZKS:
Chcesz jakieś zadanie z Aksjomatu?
To proszę:
f(x) = |x
2 − 6x + 8| + |x
2 − 6x + 5|
Podaj liczbę pierwiastków f(x) = m w zależności od parametru m.
6 sty 01:05
kylo1303: Zadam swoje 2 pytania poraz 3ci, i jedno poraz pierwszy moze teraz ktos odpowie (licze na
ciebie ZKS):
1. Czym rozni sie Aksjomat czerwony od czarnego
2. (to do studentow bardziej): czy jest jakis dzial/temat/wzory wykraczajace poza
material liceum, ale ktore spokojnie da sie samemu opanowac oraz ktore moga sie przydac w
zadaniach maturalnych. Chodzi mi o to ze czasem dobrze miec alternatywny sposob rozwiazania. Z
tego co slyszalem to sa jakies dzialania na macierzach dzieki ktorym mozna liczyc rownania z
3ma niewiadomymi.
3. Czasami spotykam sie na forum z rozwiazaniami ktore zawieraja moduły(?) "mod".
Probowalem sobie to ogarnac patrzac na zadanie (to bylo udowadnianie czegos tam) ale nie
bardzo dalo sie cos logicznie wywnioskowac. Czy ktos mi powie co to za metody/dzial?
6 sty 01:15
Godzio:
1. Czerwony ma tylko zadania rozszerzone, czarny podstawowe
2. Może macierze nie, ale wyznaczniki − do układu równań z parametrem, ale to chyba znasz
dobrze myślę ? Do matury raczej nie potrzeba większej znajomości studiów
6 sty 01:27
wójt:
1. kolorem okładki i treścią, czarny − poziom podstawowy, czerwony − poziom rozszerzony.
2. analiza matematyczna, rachunek wektorowy, wyznaczniki;
3. moduł to żargonowe określenie wartości bezwzględnej, ale pewnie chodzi Ci o "modulo".
6 sty 01:28
ZKS:
1
o Czerwony Aksjomat to poziom rozszerzony natomiast czarny podstawowy.
2
o Nie sądzę aby do matury coś ze studiów było aż tak potrzebne. Trzeba robić dużo zadań aby
złapać smykałkę (patrz
Godzio ,
ICSP ,
Vax itd.) wtedy bardziej jest
prawdopodobne że zauważysz coś co od razu Ci pomoże rozwiązać zadanie i będziesz wiedział jak
do niektórych poleceń podchodzić.
3
o mod oznacza modulo dział to chyba kongruencja jeżeli się nie mylę (algebra). Używane jest
to tak mi się wydaję do udowadniania podzielności liczb ale nie jestem pewnie musiałbyś się
spytać
Vaxa on wie o co w tym chodzi.
6 sty 01:28
6 sty 01:30
Godzio:
ZKS jest skromny, ale w nawiasie powinien siebie dopisać także
6 sty 01:35
ZKS:
Nie jestem skromny
Godzio tylko widzę co wy potraficie a co ja więc mogę tylko bić
dla was za wiedzę którą posiadacie z matematyki i oczywiście się uczyć od was.
6 sty 01:38
Godzio:
Proszę Cię
Jesteś na takim samym poziomie co my, i sobie nie zaniżaj
6 sty 01:42
ZKS:
Na tym samym poziomie wiekowym owszem ale wiedzy już niekoniecznie.
Jak tam nauka ogółem w styczniu idzie ciężko?
6 sty 01:45
Godzio:
A praktycznie 0 nauki ... obiecałem sobie, że w nowym roku siadam i wkuwam codziennie, a jak
narazie to więcej gram niż się uczę, a lada moment kolokwia i egzaminy
6 sty 01:46
ZKS:
No niestety sesja już się zbliża a teraz kolokwiami zaczynają sypać oby wszystko pozaliczać i
mieć spokój.
6 sty 01:54
Godzio: Właśnie, oby pozaliczać
6 sty 02:09
ZKS:
Pozalicza się bez problemu.
Lecę na spanie. Dobranoc
Godzio.
6 sty 02:21
Godzio: Dobranoc
6 sty 02:22
Pepsi2092: Siemano wszystkim
Możecie mi podrzucić jakiegoś linka do zadanek z jednokładnością
Takie
bardziej wprowadzające, bo dopiero zaczynam to cudo i chciałbym lepiej zrozumieć poprzez
rozwiązanie kilku zadań
6 sty 03:55
krytyk: up
6 sty 18:02
kylo1303: Apropo, dam rozwiazanie zadania od
ZKS Bo
Basiek cos sie nie garnie zeby rozwiazac
(moze nie wie)
1
o Dla m∊(−∞,3)
0 rozw.
2
o Dla m=3
nieskonczenie wiele rozw.
3
o Dla m∊(3,5)
4 rozw.
4
o Dla m=5
3 rozw.
5
o Dla m>5
2 rozw.
6 sty 18:11
Basiek: Kylo− ej, no nie widziałam tego. Czuję się okradziona −
− serio.
Pepsi− a z jakich zbiorów korzystasz, bo w ramach "dnia dobroci dla świata" ew. mogę Ci
coś zeskanować?
6 sty 18:46
ZKS:
Wszystko się zgadza
kylo1303.
6 sty 19:01
Basiek: Cholera, strasznie dużo liczenia
Ale wyszło mi. Pytanie tylko, dlaczego w tym przypadku nie liczy się dziedzina? Zachodzę w
głowę... Gdyby sprawdzać, czy coś należy/ nie należy, to rozwiązań by zdaje się nie było. Any
idea?
6 sty 19:40
ZKS:
Chodzi Ci o dziedzinę funkcji f(x) = |x
2 − 6x + 8| + |x
2 − 6x + 5|?
6 sty 19:49
Basiek: Nie, chodzi mi o dziedziny dla poszczególnych przedziałów, przy tych 5ciu przypadkach przy
rozpatrywaniu
np. dla przedziału x∊(4,5> rozwiązaniem jest x=3 co nie należy do danego przedziału, tak?
6 sty 19:52
Basiek: Dziedziną powyższej funkcji są liczby rzeczywiste, o ile się nie mylę. Możesz ze mnie nie robić
idiotki.
Dzięki wielkie
6 sty 19:53
ZKS:
Dla x ∊ (1 ; 2> ∪ <4 ; 5) wykres funkcji jest y = 3 czyli dla m = 3 mamy nieskończenie wiele
rozwiązań z przedziału x ∊ (1 ; 2> ∪ <4 ; 5).
6 sty 19:58
Basiek: Nooo, wiem
Tylko hm, chyba się nie rozumiemy. Nie wiem, czy to będzie zrozumiałe, ale
normalnie jak były jakieś funkcje, przy wszystkich wcześniejszych zadaniach jakie w życiu
robiłam, było coś takiego, że
dzieliłam na przedziały np. (−
∞,2> i x wychodził mi np. x=3 , wtedy ten x nie należał do
rozwiązania i ogólnie był pomijany.
I moje pytanie właśnie hm... bo w zasadzie wszystko mi wyszło łącznie z wykresem. Chodzi o to,
że wyliczyłam y w tych wszystkich przedziałach, a nie x? I dlatego nie sprawdzam z dziedziną?
6 sty 20:05
ZKS:
Bo Ty masz funkcję g(x) = m dla tego x nie sprawdzasz g(x) to funkcja pozioma weź sobie
długopis i ołówek lub coś innego i sprawdzasz nim ile razy Ci on przetnie wykres funkcji f(x)
(zaczynasz od dołu do góry jechać) i tak właśnie się zachowuje funkcja g(x) która będzie
jeździła dla różnych m w górę i w dół.
6 sty 20:14
Godzio:
Tak odchodząc od tematu, nie gra ktoś z was w Batelfielda 3
?
6 sty 20:16
Basiek: Łapię chyba.
Tylko, że najpierw wyliczyliśmy funkcję f(x),a potem na jej podstawie rozpatrywaliśmy g(x)=m ,
ilość rozwiązań...
Ale nieważne
6 sty 20:16
ZKS:
Ale masz oryginalnego Battelfielda 3 czy pirata?
6 sty 20:19
Godzio: Oryginalnego
6 sty 20:20
ZKS:
Bo najpierw rysujesz wykres funkcji f(x) czyli rozpatrujesz ją dla poszczególnych przedziałów
kiedy ją narysujesz wtedy sprawdzasz ile i kiedy Ci funkcja g(x) przecina f(x) tak się
sprawdza ile ma rozwiązań dane równanie.
6 sty 20:21
Basiek: Wiesz co?
My się nie dogadamy dziś
Ale i tak dzięki
6 sty 20:23
ZKS:
To dlatego możesz grać przez internet ja sobie może ściągnę najpierw a dopiero wtedy bym się
zdecydował na zakup.
6 sty 20:23
ZKS:
No niestety skoro tak mówisz to widocznie się nie dogadamy.
6 sty 20:24
Godzio:
No to jak by Ci się chciało
, z kolegami bym pograł, tylko sęk w tym, że ta gra ma wymagania
sporawe, a oni nie za bardzo mają dobre kompy/lapki, a do nowego się coś nie przykładają
6 sty 20:26
Basiek: Burzycie mit biednego, głodującego studenciny.
Idę poczytać Przedwiośnie, do potem? Lub kiedy indziej
pa
6 sty 20:28
ZKS:
Mój brat ma w miarę lapka więc dzisiaj w nocy sobie ściągnę i sprawdzę bo grałem w
Battelfielda 2 i to była naprawdę fajna gierka.
6 sty 20:32
Godzio: Też grałem w 2, dlatego i 3 kupiłem i się bardzo wciągnąłem
Fajne jest to, że jest bardzo
rzeczywista, zawsze w CoD−a grałem, ale to już przeszło
6 sty 20:34
ZKS:
MoH i CoD dobre gierki.
Ja jeszcze grałem w Battelfield Bad Company i to mnie najbardziej
wciągnęło.
6 sty 20:41
Godzio: Też dobre
W ogóle seria Batllefielda była fajna
6 sty 20:43
ZKS:
Kurde gdybym miał wcześniej trochę imieniny to już bym sobie kupił hehe.
6 sty 20:47
Godzio:
Nie ma co się spieszyć
Po sesji
6 sty 20:53
ZKS:
Po sesji to już nie będę studentem bo mnie wywalą hehe.
6 sty 20:58
Godzio:
Podobnie jak ja mówisz
To tym bardziej, będzie więcej czasu na grę hehe
6 sty 21:00
ZKS:
Dokładnie to nawet sensu nie ma żeby zaczynać się uczyć od razu można pograć.
6 sty 21:04
Godzio: Haha
W takim razie jakbyś kupił to daj znać, to się jakoś zgadamy, a ja już uciekam (pograć
sobie
)
6 sty 21:05
ZKS:
Okej jak coś to pochwalę się zakupem.
Miłego grania życzę i dużo fragów zdobytych.
6 sty 21:09
kylo1303: No coz, nawiaze do watpliwosci Basiek, moze zdolam to jakos wytluamczyc bo ewidentnie nie
rozumiesz "sedna" tego co masz wykonac (albo po prostu sie nie rozumiemy). Jak juz narysowac
wykres, to masz napisac ile rozwiazan ma f(x)=m. Czyli rozpatrujesz y (tak jakby to m,
rozpatrujemy "pionowo") i patrzysz ile "iksow" (x) spelnia danego "igreka" (y).
Bede posilkowal sie tym zadaniem:
dla m<3 (czyli tak jakby y<3)− nie ma takiego x zeby y<3 wiec nie ma rozwiazan
dla m=3 (y=3) masz w 2och przedzialach linie pozioma, czyli jest nieskonczenie rozwiazan (bo w
koncu w przedziale (1,2) mozna wybrac nieskonczenie wiele "iksow").
Dla m∊(3,5): zauwaz ze mozna wybrac 4 "iksy" zeby nasze y zawieralo sie w tym przedziale.
dla m=5 mozemy wybrac juz tylko 3 iksy.
no i dalej to tylko dwa.
Nie wiem czy rozwialem watpliwosci, ale moze przynajmniej naprowadze na rozwiazanie problemu.
6 sty 21:50
kylo1303: I jeszcze jedno:
Tam sa 3 przypadki, i niewiele liczenia xD Jesli juz to bardziej pisania bo w koncu trzeba
pisac o tych "em−ach"
6 sty 21:52
Basiek: Hm, jeszcze raz− umiem odczytać z wykresu ilość rozwiązań, naprawdę.
Problem sprawiło mi narysowanie tego wykresu na podstawie wyliczeń poszczególnych przedziałów.
6 sty 21:52
Basiek: Wiesz co?
Napiszę to łopatologicznie na kartce, o co mi chodzi i zeskanuję, ok?
6 sty 21:56
ZKS:
To czemu od razu nie pisałaś że nie wiesz jak narysować wykres?
6 sty 21:57
Basiek: Umiem
6 sty 21:58
ZKS:
Ale napisałaś że problem Ci sprawiło narysowanie tego wykresu więc o co chodzi?
6 sty 22:02
Basiek: Zaraz wrzucę skana, okej?
I wybaczcie pismo, takie mam od urodzenia niemalże
6 sty 22:02
kylo1303: AHa, to trzeba bylo tak od razu:
Wychodza ci przedzialy oraz odpowiednia wartosc f(x)
Dla x∊(−∞,1>u<5,∞) f(x)=2x2−12x+13
Dla x∊(1,2>u<4,5) f(x)=3
Dla x∊(2,4) f(x)=−2x2+12x−13
I masz normalne rysowanie wykresow. Mozesz narysowac cale parabole ale do naszego "wykresu
glownego" bedzie nalezala tylko czesc z podanych przedzialow. Osobiscie policyzlem tylko
punkty skrajne a dalej to "odrecznie".
6 sty 22:04
kylo1303: No coż, nasuwa mi sie jedynie tekst: "z kobieta to sie nie dogadasz" . Przykro mi to stwierdzic
ale w roznych momentach mowisz rozne rzeczy. I to nie problem tego ze "my sie nie rozumiemy"
tylko raczej ze ciezko u ciebie z jasnym stwierdzeniem problemu
No ale poczekajmy na scan,
moze nas wszystkich oswiecisz
6 sty 22:08
6 sty 22:08
Godzio:
Basiek przygotuj się za jakieś 1,5h zaczynamy zabawę z ciekawymi zadankami (ciekawe czyt.
nietypowe
)
6 sty 22:13
Basiek: Godzio, a może Aksjomat, co?
Muszę w końcu poprzerabiać to coś −
−
6 sty 22:14
Godzio:
Aksjomat we własnym zakresie, a z problemami zwracaj się do nas
Wracam i lecimy
6 sty 22:16
Basiek: Ech... świetnie.
Okej.
6 sty 22:16
Eta:
900 mój
6 sty 22:17
Basiek: Nie,
900 jest
Basiny
Eta się spóźniła
6 sty 22:17
Eta:
Ech .........
Basiek
6 sty 22:18
Basiek: Wiem, wiem, popsułam całą zabawę
Cała ja.
6 sty 22:18
Eta:
Dopilnuję
1000
6 sty 22:18
Basiek: Zapraszam
Tylko żeby w ogóle 1000 się pojawił
6 sty 22:19
ZKS:
Basiek ale dla x ∊ (−
∞ ; 1> ∪ <5 ;
∞) masz takie coś :
2x
2 − 12x + 13 = m.
6 sty 22:20
Basiek: No, mam?
6 sty 22:22
ZKS:
Czyli rozwiązania będą zależały od m a nie od x.
6 sty 22:23
Basiek: ale tam po prawej stronie kartki rozwiązujemy nie g(x)=m , a jedynie upraszczamy f(x), która
niewiele ma wspólnego z m na razie.
Albo ja już kompletnie nic nie rozumiem xD
6 sty 22:24
kylo1303: "f(x)=3" to "3" to jest y a nie x.
Co do pierwszego od gory:
x nalezy do (−∞,1> − dla takiego przedzialu funkcja f(x)=|x2 − 6x + 8| + |x2 − 6x + 5|
sprowadza sie do postaci: f(x)=2x2−12x+13 . Wiec te twoje miejsca zerowe nie naleza do
dziedziny. Bo gdyby x1=1,4 to juz nasza f(x)=|x2 − 6x + 8| + |x2 − 6x + 5| mialaby calkiem
inna postac.
6 sty 22:28
Basiek: Godz. 20:05
"I moje pytanie właśnie hm... bo w zasadzie wszystko mi wyszło łącznie z wykresem. Chodzi o to,
że wyliczyłam y w tych wszystkich przedziałach, a nie x? I dlatego nie sprawdzam z dziedziną?"
Godz. 22:28
" "f(x)=3" to "3" to jest y a nie x."
Dziękuję, o to mi tu chodziło.
6 sty 22:31
ZKS:
Najpierw rysujesz wykres f(x) tak jak na rysunku swoim następnie musisz sprawdzić ile i kiedy
masz rozwiązania dla f(x) = m (dla jakich
m) więc jak narysujesz wykres funkcji f(x) to
sprawdzasz ile i kiedy Ci się funkcja f(x) przetnie z wykresem funkcji y = m jak Ci pisałem
jest to wykres poziomy który będzie jeździł z dołu na górę.
Rozumiesz?
6 sty 22:31
Basiek: Od zawsze tak mam, że ja rozumiem wszystkich, a mnie to już nikt....
Cóż, trudno.
W każdym razie
dziękuję obu Jesteście genialni.
6 sty 22:32
kylo1303: Jeszcze jedno: wspomnialas ze duzo liczenia: nie trzeba bylo za kazdym razem mnozyc, zauwaz ze
oryginalnie masz juz postac "wymnozona". Przy rozpatrywaiu przedzialow trzeba bylo sobie
rozlozyc na czynniki, ale potem to juz korzystac z postaci oryginalnej.
6 sty 22:35
kylo1303: A czego w pierwszym masz "brak rozwiazan" ? Chodzi ci ze dla m∊(−∞,3) jest 0 rozwiazan?
6 sty 22:36
kylo1303: Tzn skad to wzielas.
6 sty 22:36
Basiek: Chodzi Ci o to, że narysować na jednym wykresie te dwie kwadratowe i na tej podstawie robić?
6 sty 22:36
Basiek: No, ponieważ na wykresie brak jest rozwiązań dla tego przedziału? Oo
6 sty 22:37
kylo1303: Czyzby? Przykladowo dla x=1 jest 3, dla x=0 13, dla x=−1 → 27. Wiec rozwiazania sa nawet na tym
wykresie. ale dla y∊(−∞,1) to juz sie zgodze.
6 sty 22:41
Godzio: Eta nabijemy tysiaka w nocy jak Ciebie nie będzie
6 sty 22:42
Basiek: Aaaaaaaaaa, widzę o co Ci chodzi
tam, gdzie jest g(m) poprawiłam na m= , a w tej klamrze faktycznie, tam gdzie pisze m, ma być
x
Od dziś literki będą mnie prześladować
6 sty 22:44
kylo1303: Hmmm... wydaje mi sie ze wlasnei zmienilas na zle. W tej klamrze po lewej na dole ma byc
m
a nie x. Jakby byl x to by ci glupoty wyszly.
6 sty 22:47
kylo1303: Dobra, ja juz koncze o tym. Jesli chcesz to pytaj, ale sam nic nie bede nawiazywal.
6 sty 22:48
Godzio:
Dobra jak skończycie to denne zadanie to dajcie znać, dam coś ciekawszego (
kylo nie bój
się, to nie będzie zadanie kilkudniowe
)
6 sty 22:48
Basiek: Kylo, szczerze to mam teraz "lekki" mętlik z tymi oznaczeniami.
trudno. Może po
weekendzie dopadnę matematyczkę, czy coś
6 sty 22:52
Godzio: 1. Niech a i b będą liczbami rzeczywistymi. Udowodnij, ze jeśli ax2−ax−b < 0 dla każdego
rzeczywistego x, to również |x − a| + b > 0 dla każdego x ∊2 R.
6 sty 22:55
ZKS:
Zrobiłem.
6 sty 23:03
Godzio:
Eee Ty się nie liczysz
6 sty 23:03
Basiek: Poddałam się?
6 sty 23:04
Godzio: ZKS co masz teraz na analizie ? Zarzucę Ci czymś bardziej matematycznym
6 sty 23:05
kylo1303: Dobra, chwile mnie nie bylo ale zaraz biore sie do roboty. Dzieki ze mnie uspokoiles z tym
zadaniem xD
6 sty 23:08
kylo1303: eee co oznacza x∊2R ?
6 sty 23:09
Godzio: 2 się tam sama wkradła, nie powinno jej tam być
6 sty 23:10
Basiek: Ja założyłam, że nie trafił w klawiaturę..
6 sty 23:10
ZKS:
Ja już się całkuję.
Dzisiaj mnie cała noc czeka z kreską ale jakieś łatwiutkie zadanie
mógłbyś podać to w między czasie będę sobie robił.
6 sty 23:10
kylo1303: No to dam pierwsza czesc:
jesli a=0 to jest bannal bo b>0 i |x−a|≥0 . Teraz jeszcze dla a<0
6 sty 23:13
Godzio: Niech funkcja f(x) będzie monotoniczną funkcją różniczkowalną, a f
−1(x) jej funkcją
odwrotną. Dowieść, że jeżeli
∫f(x)dx = F(x) + C, to
∫f
−1(x)dx = xf
−1(x) − F(f
−1(x)) + C.
Akurat może mi zrobisz zadanie z listy
6 sty 23:14
ZKS:
kylo1303 przecież z tego ax
2 − ax − b < 0 wiadomo że a < 0 i właśnie wystarczyło
udowodnić że b > 0.
6 sty 23:15
Basiek: Tylko tyle, to przecież z delty wyszło na początku−− Żadnych przekształceń, wyliczania x?
Przekształcania, podnoszenia do kwadratu?!
6 sty 23:17
ZKS:
Godzio znaczy chciałem powiedzieć że ja nie dawno zespolone zacząłem.
Oczywiście
zobaczę czy coś w ogóle uda mi się z tym zrobić.
6 sty 23:20
kylo1303: No to wiem przeciez. Teraz staram sie to udowodnic.
6 sty 23:20
Basiek: a2+4ab<0
a(a+4b)<0⇔
a+4b>0, bo wiemy, że a<0
4b>−a , a <0, stąd −a>0, więc b>0
cnu.
6 sty 23:23
Godzio:
f(0) = − b < 0 ⇒ b > 0, zatem |x − a| + b > 0 c.n.d
6 sty 23:25
ZKS:
Ale już zrobiłeś to zadanie udowodniłeś to co trzeba było.
6 sty 23:25
Basiek: Godzio.... no ładnie tak w jednej linijce , ech. Też tak chcę.
6 sty 23:26
ZKS:
Rób dużo zadań a będziesz robiła.
6 sty 23:27
kylo1303: Widze ze zostalem wyprzedzony. Teoretycznie zrobilem jak Basiek, ale jak patrze na to co
napisal Godzio to pukam sobie w glowe. x=0 (z reszta tak samo jak x=1) sprawdzilem na
samym poczatku, oczywiscie wyszlo mi b>0 ale jakos uznalem ze b jest zmienna i moze przyjmowac
rozne wartosci dla roznych x....
6 sty 23:28
Basiek: Jasne.
Równie dobrze mogę Ci powiedzieć, żebyś nauczył się fruwać. Powodzenia.
6 sty 23:28
Godzio: No to podobne:
Niech a i b beda liczbami rzeczywistymi. Udowodnij, że jeśli ax2−ax−b < 0 dla kazdego
rzeczywistego x, to również
x2 + 3 + 3a2b|x| > 33√2x2
dla każdego x ∊ R
6 sty 23:29
Godzio:
kylo jasne, że b przyjmuje różne wartości, ale nas interesuje, że jest dodatnie
6 sty 23:30
kylo1303: "kylo1303 przecież z tego ax2 − ax − b < 0 wiadomo że a < 0 i właśnie wystarczyło
udowodnić że b > 0."
A co do tego: jesli wykazesz ze b>0 to tak. Ale jako ze zaczlem rozpatrywac "a" to mialem 2
mozliwosci: funkcje kwadratowa o a<0 i Δ<0 lub funkcje liniowa stala o (−b)<0.
6 sty 23:30
kylo1303: No tak, ale "b" nie jest zmienna w tym rownaniu, a tak mi sie zakodowalo w glowce.
6 sty 23:31
Godzio:
Chyba, że tak
6 sty 23:32
ZKS:
Godzio chcesz jedno zadanie z kreski (jedno z pierwszych jakie mieliśmy do kreślenia)?
6 sty 23:35
Godzio:
Nie nie
Wiem co to jest, widziałem jak kolega to kreślił, teraz robił przez 5 h jakiegoś
torusa
, wole bardziej matematyczne zadania
6 sty 23:36
ZKS:
Dam Ci akurat takie matematyczne związane ze stereometrią.
A matematyczne jakąś nierówność
Ci mogę dać do udowodnienia.
6 sty 23:39
Godzio: No to dawaj
6 sty 23:39
kylo1303: No to jesli chodzi o tamto zadanie to b>0. Podnosze do 3, po rozpisaniu bede mogl skrocic
54x2 wiec wyjdzie mi L>0 (a wszystko jest dodatnie). Jeszcze ewentualnie sprawdze dla zer.
6 sty 23:41
kylo1303: Sory, tam jest 3 wiec nie musze jednak sprawdzac.
6 sty 23:42
ZKS:
Z kreski chcesz czy nierówność?
6 sty 23:43
Godzio: No nie wiem z czego sobie skrócisz 54x
2
6 sty 23:43
Godzio:
@ZKS
I to i to
6 sty 23:43
kylo1303: Jednak skroce tylko 27 xD Zastanawiam sie czy rozpisywanie to dobra droga, bo chyba nie
6 sty 23:47
Godzio:
Podpowiem, że w rozwiązaniu nie trzeba nic podnosić do kwadratu
6 sty 23:47
ZKS:
Geometria:
Wykreślić trzy rzuty sześcianu ABCDA
1B
1C
1D
1 o boku a = 4 cm, którego
przekątna AC
1 jest prostopadła do rzutni poziomej π
1 zaś przekątna ściany
bocznej CB
1 tworzy z rzutnią π
2 kąt α = 15
o.
Nierówność:
a , b , x , y ∊ R
+ ∧ a
5 + b
5 ≤ 1 ∧ x
5 + y
5 ≤ 1 to a
2x
3 + b
2y
3 ≤ 1.
6 sty 23:48
Godzio:
Biorę karteczkę i robię nierówność, to z geometrii chyba nie na mój poziom
6 sty 23:51
kylo1303: To moe troche inaczej to zrobic:
Jesli x∊(−1,1) to wtedy xn jest zawsze mniejszy od 1. Wtedy moge wykazac ze jedno jest wieksze
od 0 bo jest 3jka (dodam ze n jest zawsze parzyste w tym wypadku lub gdy jest nieparzyste to
podstawa jest dodatnia).
jesli |x|>1 to wtedy xn jest wiekszy od xn−1 i wtedy przykladowo gdybym mial 27x6>27x2 xD
Mogloby byc czy za duzo kombinowania?
6 sty 23:52
Godzio:
Za dużo, pomijając, że mało z tego rozumiem
6 sty 23:53
Pepsi2092: Hello my friend
Basiek już sobie ogarnałem tą jednokładność zaczynając od zera i od
podstawowych zadań ze zbioru A.Kiełbasy, teraz przechodzę do aksjomatu więc zobaczymy na ile
się wyumiałem
Dlatego wielkie dzięki i nie musisz nic skanować
6 sty 23:54
Basiek: Zgubiłeś 's'
Ponadto cieszę się, szczerze
6 sty 23:56
ZKS:
To weź też drugą do robienia kresek.
6 sty 23:57
Pepsi2092: Faktycznie wybaczcie
Tym bardziej nie chcę podpaść dzisiaj chłopakom bo wiem, że mają dla
mnie jakiś ciekawy przykład z wykazywaniem
6 sty 23:59
Basiek: Jestem przekonana, że owszem.
Ja się dystansuję, czytam "Przedwiośnie"− swoją drogą,
genialne
7 sty 00:01
ZKS:
Ach pamiętam Cezary Baryka i spółka.
7 sty 00:03
Basiek: Póki co bez spółki, jedynie z Hipolitem
7 sty 00:05
kylo1303: Dobra Godzio, chyba wezme sie za wlasne zadanka. Stwierdzilem ze moje myslenie nad
zadaniem jest po prostu zle i wszystkie sposoby rozwiazywania ktore podejmuje koncza sie na
rozpisywaniu na przypadki, co zapewne jest bledne. Jako ze za twoja wskazowka do potegi nie
bede podnosil wiec skonczyly mi sie koncepcje. Moze bledne jest tez to ze z zalozenia w ogole
nie korzystalem (oprocz tego ze b>0), jak ktos rozwiaze to sobie zobacze.
7 sty 00:09
Godzio:
Pokazać rozwiązanie ?
7 sty 00:10
kylo1303: Kwestia innych, mnie to wisi bo juz dzisiaj do tego nie siadam bo mi sie nie chce.
7 sty 00:12
Basiek: Daaaaj.
7 sty 00:13
Godzio: @
ZKS naciągane rozwiązanie Twojej nierówności
a
5 + b
5 ≤ 1
x
5 + y
5 ≤ 1
a
5x
2 + a
5y
5 + b
5x
5 + b
5y
2 ≤ 1
a
5x
5 ≤ 1 − (a
5y
5 + b
5x
5 + b
5y
2)
| | 1 | |
a2x3 + b2y3 = |
| * a5x5 + b2y3 ≤ |
| | a3x2 | |
| 1 | |
| (1 − (a5y5 + b5x5 + b5y2) ) + b2y3 = |
| a3x2 | |
| 1 | | y5 | |
| (1 − b5x5) − |
| (a5 + b5) + b2y3 ≤ 1, wytłumaczenie: |
| a3x2 | | x2x3 | |
Z początkowych warunków wiemy, że a,b,x,y < 1, zatem:
1 − b
5x
2 jest ujemne, więc:
| 1 | | y5 | |
| (1 − b5x5) − |
| (a5 + b5) < 0 |
| a3x2 | | x2x3 | |
b
5y
3 < 1
Zatem suma całości musi być na pewno ≤ 1
7 sty 00:16
Godzio:
ax2 − ax − b < 0, jak słusznie zauważyłeś b > 0 (dla x = 0 widać to bardzo dobrze)
Zatem:
[korzystam ze średnia arytmetyczna ≥ geometryczna ]
x2 + 3 + 3a2b|x| = x2 + 1 + 2 + 3a2b|x| ≥ 33√x2 * 1 * 2 + 3a2b|x| =
= 33√2x2 + 3a2b|x| > 33√2x2 ponieważ, 3a2b|x| > 0
7 sty 00:18
Basiek: Ja normalnie muszę to skomentować.
"AHA"
7 sty 00:25
Basiek: A mogę ja zarzucić zadaniem?
Rozwiąż równanie w zbiorze liczb naturalnych
a
x+(2a+1)
y=(a+1)
z dla a∊N/{1} i x,y,z∊N∪{0}
Jak się domyślacie, ja nie wiem
7 sty 00:36
Godzio:
To kojarzy mi się tylko z jednym: Wielkie twierdzenie Fermata
(nie trzeba wiele liczyć,
jedynie trzeba sprawdzić przypadki jakieś, raczej mało ich będzie)
Tak mi się wydaję na pierwszy rzut oka
7 sty 00:41
Godzio:
Inaczej, z tego twierdzenie wiemy, że:
Dla: x,y,z > 2 Równanie nie zachodzi
Więc trzeba sprawdzić co się dzieje, dla x,y,z = 0, 1, 2 w różnych kombinacjach
7 sty 00:43
Basiek: dla X
n + Y
n = Z
n
brak rozwiązań w zbiorze naturalnym <− to twierdzenie... ja tu widzę podobieństwo takie, że mam
xyz, mam 3 wyrazy, 3 potęgi... i dodawanie.
7 sty 00:45
Godzio:
Hmmm, jakieś 18 przypadków trzeba sprawdzić
7 sty 00:50
Basiek: Hm, 18?
x,y,z∊{0,1,2}
czyli 3
3= 9
7 sty 00:53
Basiek: Boże...3
3= 27 <geniusz>
7 sty 00:54
wójt:
7 sty 00:57
wójt:
7 sty 00:57
wójt:
7 sty 00:57
wójt:
7 sty 00:57
wójt:
7 sty 00:57
wójt:
7 sty 00:57
wójt:
7 sty 00:57
wójt:
7 sty 00:57
wójt:
7 sty 00:57
wójt:
Mój jest tysiąc
7 sty 00:57
Basiek: Cóż, desperaci są wśród nas...
7 sty 01:00
Godzio:
1. x = 0, y = 0, z = 0
2. x = 1, y = 0, z = 0
3. x = 2, y = 0, z = 0
4. x = 0, y = 1, z = 0
5. x = 0, y = 2, z = 0
6. x = 0, y = 0, z = 1
7. x = 0, y = 0, z = 2
8. x = 1, y = 1, z = 1
9. x = 2, y = 1, z = 1
10. x = 1, y = 2, z = 1
11. x = 1, y = 1, z = 2
12. x = 2, y = 2, z = 2
No Tylko 12
7 sty 01:06
Basiek: 221 ?
201 ?
210 ?
...
7 sty 01:10
Godzio:
A no tak
Ja już se daje spokój, beznadziejne zadanie
7 sty 01:10
Basiek: 101?
012?
021?
7 sty 01:11
Godzio:
Basiek powodzenia w sprawdzaniu 27 przypadków
7 sty 01:13
7 sty 01:13
Basiek: Przynajmniej dobrze obliczyłam, że jest ich 27. Dla mnie to już jakiś sukces
7 sty 01:13
kylo1303: Odnosnie twojego zadania:
Przeanalizowalem odpowiedz i stwierdzam ze jest dobra. I to tyle co moge powiedziec. Nie bedzie
zadnego "bylem blisko" ani nawet "a myslalem zeby tak zrobic" ani zadnego z innych podobnych
stwierdzen.
7 sty 01:19
Basiek: Oj tam, Ty przynajmniej przeanalizowałeś zadanie, a ja po wyrażeniu "średnia...>średnia..."
pomyślałam "Aha, fajnie"
i odpuściłam
Kylo swoją drogą, widać, że masz gorszy dzień
7 sty 01:25
kylo1303: Az tak? Nie moge sie z tym nie zgodzic, ale nie sadzilem ze bedzie to widac
7 sty 01:35
kylo1303: Ale zaraz porobie zadanka z Aksjomatu to sie odkuje xD
7 sty 01:36
Basiek: Hm, powiedzmy, że żali mi się cały świat i wyczuwam na kilometry tego typu stan
Udzielam
świetnych porad w każdej dziedzinie podobno, jakby coś
7 sty 01:37
Godzio:
Pani psycholog
?
7 sty 01:38
Basiek: NIGDY. Boże uchowaj.
Nie mam pojęcia, mam coś takiego w sobie, że wszyscy mi wyjawiają swoje tajemnice, żalą mi
się...
a ja hm, naprawdę udzielam świetnych rad. Z pewnością, gdybym sama się do nich stosowała
moje życie byłoby idealne
7 sty 01:41
Godzio:
Przydałaby mi się osoba, która ma świetne rady
7 sty 01:42
kylo1303: Ale wyczuwam tutaj probe doszukania sie podloza emocjonalnego. A ja po prostu mam gorszy dzien.
Wstalem o 16, z czego nie bylem zadowolony, przez caly dzien gralem na komputerze... złamalem
jedno ze swoich postanowien na dzien dzisiejszy, co tez radosci mi nie sprawilo. Tak wiec
ogolnie sprowadza sie to do tego ze nie jestem zadowolony ze swoich dzialan= mam gorszy humor.
Ot cala filozofia. A do tego
Godzio sypie trudnymi zadaniami
(wiem wiem, sa banalne, a
moja definicja zadania trudnego nijak sie ma do rzeczywistosci)
7 sty 01:43
Godzio:
Hehe, nie jest najgorzej
kylo Jakie ja miałem plany, a coś ostatnio ciężko mi je
realizować
7 sty 01:44
Basiek: Godzio , jak coś, jestem do dyspozycji.
Całodobowo za wyjątkiem ranków
Kylo niezadowolenie jest stanem emocjonalnym tak w nawiasie.
I fakt faktem, wyglądasz
na rozdrażnionego, nie smutnego, ani złego. Pytanie, czy nie jesteś dla siebie zbyt surowy,
bo naprawdę ciężko pracujesz.
Po prostu należy Ci się odpoczynek. A gdyby
Twój organizm nie potrzebował spać do 16, to byś tyle nie spał, po prostu
http://komixxy.pl/1056790/Ewolucja
Na "pocieszenie"
7 sty 01:47
Godzio: Hmmm ciekawe
7 sty 01:50
kylo1303: to teraz wracajac do tematu, mam zadanie:
Narysuj wykres funkcji:
y= − |log2|x−3||+1
Jest jakis sposob oprocz podstawiania liczb oraz rozpatrywania przypadkow?
7 sty 02:01
Basiek: Wow
To wiem.
Rysujesz sobie log
2x, potem przesuwasz 3 jednostki w lewo, całość odbijasz nad oś OX, potem
całość pod oś OX, a na koniec podnosisz całą funkcję o 1 jednostkę do góry.
Tadam!
7 sty 02:03
Godzio:
Basiek, jak wiesz to popraw swoje rozwiązanie
7 sty 02:07
Basiek: * o 3 w prawo.
Myślę co innego, piszę co innego. Cała ja
7 sty 02:08
Godzio:
Tego akurat nie miałem na myśli, ale dobrze, że to też dojrzałaś
7 sty 02:09
Godzio:
Zapiszę Twoje przekształcenia:
log2x → log2(x − 3) → |log2(x − 3)| → − |log2(x − 3)| → − |log2(x − 3)| + 1
To jest to samo co końcowa ?
7 sty 02:10
Basiek: I jeszcze logarytm na prawo odbijamy ze względu na moduł przy argumencie.
Fajna funkcja
Można tu niemal wszystkie przekształcenia zastosować
7 sty 02:11
Godzio:
To wsadź to w dobre miejsce to przekształcenie
7 sty 02:12
Basiek: Już sama zauważyłam
Przekształcanie funkcji to jeden z tematów, które "raczej umiem", bo
miałam kiepską ocenę z tego ze sprawdzianu.
7 sty 02:12
Basiek: Rysujesz sobie log2x, potem przesuwasz 3 jednostki w prawo, potem odbijasz całą tę funkcję na
prawo, teraz całość odbijasz nad oś OX, potem całość pod oś OX, a na koniec podnosisz całą
funkcję o 1 jednostkę do góry.
Tadam!
7 sty 02:13
Godzio:
Dalej coś nie pasi
7 sty 02:14
Basiek: Poddaję się
7 sty 02:16
Godzio:
Taka kolejność powinna być:
log2x → log2|x| → |log2|x|| → −|log2|x|| → −|log2|x − 3|| + 1
Z tym, że przesunięcie o wektor może być rozdzielone na 2 przesunięcia, ([3,0] i [0,1] )
i |f(x)| oraz f(|x|) może być stosowane zamiennie, tzn. nie ważne które będzie pierwsze
7 sty 02:18
Basiek: No ok, a dlaczego nie mogę odbić na prawo już po przesunięciu o [3,0] ? −−
7 sty 02:19
Godzio:
Podstawa: 98
Rozszerzenie: 94
7 sty 02:20
Godzio:
Bo najpierw trzeba wsadzić wartość bezwzględną na x, a potem dopiero przesunięcie
7 sty 02:21
Basiek: Godzio bowiem jesteś moim "miszczem", wiedz to.
7 sty 02:21
kylo1303: No ogolnie to umiem przeksztalcenia. Bardziej myslalem z poczatku o rozpisaniu tego, ale spoko,
i tak dzieki.
7 sty 02:21
Basiek: Czy to wtedy nie będzie −Ilog2IxI−3I+1 ?
7 sty 02:22
Godzio:
Basiek Twoimi przekształceniami tak, warto dodać −|log2(|x| − 3)| + 1
7 sty 02:24
Godzio:
Hehe ciekawe jakby to było zorganizować zlot "fanów matematyki.pisz"
7 sty 02:25
Basiek: No to chyba jednak nie rozumiem tych przekształceń, brawo ja
7 sty 02:25
Basiek: Dziwnie!
7 sty 02:25
Godzio:
No bo jeśli masz przesunięcie o wektor (chodzi o pierwszą współrzędną) to ona włazi do x zawsze
Mamy x2 → [1,0] → (x − 1)2
|x| → [1,0] → |x − 1| itd.
Ale jeśli mamy wartość bezwzględną to jest różnica:
f(x) = x + 3 → f(|x|) → |x| + 3 → [1,0] → |x − 1| + 3
czy
f(x) = x + 3 → [1,0] → x − 1 + 3 = x + 2 → f(|x|) → |x| + 2
prawda ?
7 sty 02:27
Basiek: Ups.
ILUMINACJA i stała się światłość...
7 sty 02:30
kylo1303: Dam swoje przeksztalcenia:
log2|x|→|log2|x−3||→−|log2|x−3||→−|log2|x−3||+1
7 sty 02:32
Godzio:
Są ok
7 sty 02:32
kylo1303: 1. log2x=log2|x|
2. odbilem i przesunalem w prawo o 3
3. odbicie od osi OX i podniesienie o 1
7 sty 02:34
kylo1303: hmmm... zadanie zrobilem zle (tzn po czesci). Blad polegal w tym:
Jak mamy log2x to przeciez x>0, ale przeciez log2|x| to dziedzina jest R\{0}
7 sty 02:43
kylo1303: sory za 2x "przeciez". Blad napisalem bo moze i wy o tym zapomnieliscie.
7 sty 02:44
Godzio:
W takim razie na czym błąd polegał ? Wykres rysujemy etapami, i jedynie początek nas
interesuje, a co się potem z dziedziną dzieje, to już nie zwracamy uwagi
7 sty 02:45
Basiek: Mądra uwaga
Przy zerze trzeba wykropkować, czy jak to tam ująć
7 sty 02:47
Basiek: Pytanie: Gdyby hm... np x≠3 i wiecie no... odbiła np. na lewo, to czy musiałabym "wykropkować"
(?) wykres w tym samym miejscu po stronie odbicia? O.o
7 sty 02:48
Godzio:
No raczej, że tak
7 sty 02:49
kylo1303:
Tzn blad polegal na tym ze rysowalem tylko po prawej stronie osi OY, a trzeba bylo po obu.
(wykres oczywiscie nie odpowiada temu w zadania, ale ogolnie wiadomo o co chodzi)
7 sty 02:50
Godzio:
Mówimy o czymś takim ?
N − przed odbiciem
Z − po odbiciu
7 sty 02:51
Godzio:
Tak, bo |x| nie wymazuje nam prawej strony
7 sty 02:52
7 sty 02:52
Basiek: √x chyba też nie?
tylko Moduł na całości i minus na całości, prawda?
7 sty 02:55
Godzio:
Nie za bardzo wiem o co chodzi, może to przez to, że zasypiam
7 sty 03:00
Basiek: Nieważne
Dobranoc?
7 sty 03:02
Godzio:
No fajnie by było
7 sty 03:03
kylo1303: Ja jeszcze troche posiedze (patrzac na to ze wstalem o 16 to chyba nic dziwnego). Tyle ze
raczej zajme sie swoimi sprawami (film czeka
) Ale bede zagladal, bede jak superman (albo
polska sluzba zdrowia)− zawsze w pogotowiu!
7 sty 03:05
Godzio:
Hehe, ok, w takim razie dobranoc
7 sty 03:06
Basiek: Hahaha
Cudnie
To nie jest też moja godzina, poczytam jeszcze trochę, aczkolwiek w takim
tempie mogę nigdy nie skończyć
7 sty 03:06
Trivial: Gratuluję przekroczenia granicy tysiąca postów! Teraz już tylko 10000 zostaje.
7 sty 11:16
Basiek: Dzieci moje drogie, to może jakieś 2 zadanka z Aksjomatu? Bo póki co nie zrobiłam dziś
kompletnie NIC... Co mnie trochę martwi
7 sty 18:12
kylo1303: Tak od razu po wstaniu do zadan? xD Moge ci cos podrzucic, tylko powiedz z jakiego dzialu
7 sty 18:25
ZKS:
Wyznacz wartości parametru m ∊ ℛ dla których równanie:
(x
2 − 2x + m − 2)(|x − 1| − m + 1) = 0
ma trzy różne pierwiastki rzeczywiste. Oblicz te pierwiastki.
7 sty 18:34
Godzio:
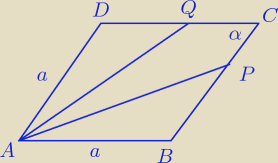
No to taki banalik do Godzia
Romb ABCD o boku długości a i kącie ostrym α podzielono na trzy części o równych polach (jak na
rysunku) Wyznacz długość AP oraz AQ
7 sty 18:36
Basiek: Dobra, ukąpałam się.
Eeeee, dzięki, wszystkim.
Kylo, wypraszam sobie, obudzono mnie gdzieś po 12
Zrobię to... za jakiś czas, znaczy postaram się dziś.
I nie dotykać, bo ugryzę!
7 sty 18:49
kylo1303: Heh, to ja wczoraj poszedlem o 7.30 spac. A ktorego ci nie ruszac? Obu?
7 sty 18:53
Basiek: Obu.
Przez Ciebie popadam w kompleksy, serio! Pewnego dnia powieszę się na klamce, a Ciebie nawet
nikt nie będzie w stanie powiadomić, żebyś miał wyrzuty sumienia
Dlatego nie ruszaj. Naprawdę gryzę
7 sty 18:56
Godzio:
To kylo nam się zanudzi, masz tutaj takie zadanie:
Ciąg arytmetyczny (an) ma 19 wyrazów. Wiedząc, że S19 = 437, oblicz:
a) środkowy wyraz
b) 8 + a9 + a10 + a11 + a12
7 sty 19:02
Godzio: Miałby być a8
7 sty 19:02
kylo1303: Spoko, zaraz zrobie. A co twojego zadania mam odpowiedz, ale nie wiem czy o taka forme
chodzilo. Podam TYLKO FORME ODPOWIEDZI:
AP=x√y gdzie x i y to jakeis liczby (znane)
7 sty 19:07
Godzio:
O taką
7 sty 19:08
kylo1303: a) 23
b) 115
7 sty 19:11
Łukasz: to może znajdzie się chętny aby rozwiązać coś takiego:
7 sty 19:11
Godzio: Szybki jesteś, może coś trudniejszego znajdę
7 sty 19:12
kylo1303: Ogolnie ciagi to raczej moja mocna strona, czego nie moge powiedziec o geometrii.
7 sty 19:13
Godzio:
Wyznacz współrzędne punktu P leżącego na wykresie funkcji y = 7x − x2 −15, dla którego
suma odległości od osi układu współrzędnych jest najmniejsza.
Nie chodzi mi o odpowiedź, a o całe rozwiązanie, bo tutaj można na wiele rzeczy nie zwrócić
uwagi,
Łukasz pisz w swoim temacie
7 sty 19:14
ZKS:
Pamiętam to zadanie.
7 sty 19:19
Godzio:
7 sty 19:20
kylo1303: Dam odpowiedz, jesli jest ok to bede pisal rozwiazanie:
Odp. P(3,−3) (x=3 y=−3
poprawne?
7 sty 19:24
Basiek: Godzio, dobrze mi się wydaje, że AP= AQ?
7 sty 19:29
kylo1303: Dobrze ci sie wydaje.
7 sty 19:30
Godzio: Poprawne
7 sty 19:30
Basiek: | | 2 | | 5 | |
wyszło mi coś takiego: hm √ |
| a2( |
| −cosα) |
| | 3 | | 3 | |
Pierwiastek jest nad całością.
7 sty 19:31
Godzio:
A wynik jest nieco inny
7 sty 19:33
Godzio:
| | a | |
Powinno być |
| √13 + 12cosα po uproszczeniu |
| | 3 | |
7 sty 19:34
Basiek: Już wiem, co mam źle...
| | 1 | |
do wzoru na pole rombu dodałam na początku |
| czyli u mnie standard |
| | 2 | |
7 sty 19:37
kylo1303: No wiec napisze krok po kroku:
1. y=−(x
2−7x+15) − znajduje x
w i rysuje sobie funkcje.
2. Latwa zauwazyc, ze dla x>x
w suma odleglosci wspolrzednych bedzie sie powiekszac. To samo
| | 1 | |
jest dla x<0. Wiec przedzial ktory mnie intereseuje to x∊<0,3 |
| > i tutaj musze szukac |
| | 2 | |
rozwiazan,
3. Funkcje S(x)=|y|+|x| (suma odleglosci). Z podpunktu 2 widze jednak ze x>0, a y<0 , zatem
moge przedstawic moja funkcje jako S(x)=x−y. Wiem rowniez ze moj punkt P(x,y) zawiera sie an
prostej y=−(x
2−7x+15).
4. Podstawiam do funkcji S(x) "y", otrzymuje S(x)=x+(x
2−7x+15)=x
2−6x+15
Aby suma |x| i |y| byla najmniejsza, wartosc funkcji S(x) musi byc najmniejsza. Funkcja ta jest
rosnaca, wiec najmniejsza wartosc przyjmuje w wierzcholku.
| | 6 | |
xw= |
| =3 wiec y=−(9−21+15)=−3 |
| | 2 | |
7 sty 19:38
kylo1303: Co do zadania z rombem to mam taki sam wynik ajk podales Godzio
7 sty 19:39
suzi: (log7 14−log log7 2√7 )(log10 1/2−log10 5)/ (log√3 1/ 27−log √2 1/ 81)=
7 sty 19:40
Basiek: | | 1 | |
Po zlikwidowaniu |
| mnie też wyszło. |
| | 2 | |
Btw. pierwszy raz
ZKS wrzucił trudniejsze zadanie od
Godzia
7 sty 19:42
Godzio:
Ok, jeśli wszystko tak byś komentował to jest dobrze.
7 sty 19:43
Godzio:
Bo non stop mnie obrzucacie błotem, że za trudne daje
7 sty 19:44
Basiek: Wiecie co? Idę po kawę.
7 sty 19:45
Godzio: Ok, 1100 jest mój
7 sty 19:45
kylo1303: No to w takim razie ja pojde cos zjem. A potem zajme sie zadaniem od ZKS. Jednak nie bede
nic pisal dopoki Basiek nie pozwoli xD
7 sty 19:48
Basiek: Zimne kakao
Dobra, pytanie:
w zad. od ZKS naprawdę muszę rozpatrywać przypadek:
a) gdy funkcja 1. ma 2 miejsca zer. , a druga 1
b) gdy obie mają po 2 miejsca zerowe
c) gdy pierwsza ma 1 miejsce zerowe, a druga 2 ?
Toż to kupa roboty jest...
7 sty 19:51
Godzio:
Zadania ciekawe:
1. Ile jest takich czterocyfrowych liczb podzielnych przez 11,których cyfrą setek i cyfrą
jedności jest 8? Podaj najmniejszą oraz największą liczbę o tej własności.
2. Uzasadnić, że jeśli liczba n nie jest podzielna przez trzy to reszta z dzielenia kwadratu
liczby n przez trzy jest równa jeden.
7 sty 19:51
Godzio:
Basiek a kto powiedział, że nie będzie roboty
Pamiętaj, mają być różne
7 sty 19:53
Basiek: Jak już wyliczę, to sobie sprawdzę jakie są...
O ile kiedykolwiek to wyliczę. Zaczynam "znielubiać" parametry.
7 sty 19:55
Basiek: Godzio− min. to będzie 7897?
7 sty 20:01
kylo1303: 1. jest 5 takich liczb. Najmniejsza to 1848 a najwieksza to 5808
7 sty 20:02
Basiek: tfu
7898
7 sty 20:02
Basiek: wow
Nie no, mam dość
7 sty 20:03
Basiek: Ale wiesz, jeśli moja spełnia warunki , a jest większa niż Twoja, to znaczy, że oboje mamy źle
7 sty 20:04
kylo1303: 2. Jesli jest niepodzielna to mam 2 mozliwosci zapisania tej liczby:
3n+1 lub 3n+2
1. 3n+1 :
(3n+1)2=9n2+6n+1=3(3n2+2n)+1
2. 3n+2
(3n+2)2=9n2+12n+4=3(3n2+4n+1)+1
7 sty 20:05
Godzio:
Nie mam do tego odpowiedzi
Ale zaraz zobaczę jak wychodzi
7 sty 20:05
Godzio: kylo w 2 właśnie o to chodziło
7 sty 20:06
kylo1303: Wedlug mnie twoja nie spelnia
7 sty 20:06
Basiek: I hm, min to będzie faktycznie 1848, max. 9878, a ile ich jest, to ja nie mam pojęcia.
7 sty 20:06
kylo1303: Aha, poprawilas juz. No i dizeki temu widze swoj blad xD
7 sty 20:06
kylo1303: Bedzie 8 liczb, najmniejza to 1848 a najwieksza to 9878
7 sty 20:08
Godzio:
A taka: 9878 ?
7 sty 20:08
Godzio:
No właśnie
7 sty 20:08
Basiek: 4 takie liczby?
7 sty 20:08
kylo1303: Tak wlasnie mi sie wydawalo ze 5808 to troche za malo bo w koncu to niewiele ponad polowa z
9999
7 sty 20:09
kylo1303: 1848
2838
3828
4818
5808
7898
8888
9878
7 sty 20:10
Basiek: To jednak nie 4
hahaha.
Kylo. jak liczyłeś?
7 sty 20:10
kylo1303: Z cechy podzielnosci przez 11
7 sty 20:11
Godzio:
Liczba 4 cyfrowa: abcd gdzie b = d = 8
a8c8 z cechy podzielności mamy, że liczba a − 8 + c − 8 musi dzielić się przez 11 zatem może
przyjmować takie wartości:
a + c − 16 = − 11
a + c − 16 = 0
a + c = 5 (1,4) (2,3) (3,2) (3,1) (5,0)
a + c = 16 (7,9) (8,8) (9,7)
Łącznie 8
7 sty 20:11
Basiek: Domyśliłam się....
(a+b)−16 podzielne przez 11
7 sty 20:11
Basiek: aha...
Godzio− dlaczego wszystko wygląda u Ciebie tak cholernie prosto?
7 sty 20:12
kylo1303: Bo akurat te 2 to byly proste. No ale tu sie zgodze, czlowiek ma obliczenia na pol kartki a
tutaj rozwiazanie w jednej linijce...
7 sty 20:15
Basiek: Boże, ja naprawdę jestem humanistką.
7 sty 20:16
Godzio:
No dobra, wszystko dzisiaj robicie, za dobrze wam idzie
Zróbcie to od
ZKS
7 sty 20:18
kylo1303: Taka poprawka:
** Proste jesli znasz ceche podzielnosci przez 11
7 sty 20:18
kylo1303: No ja ide jesc zeby z glodu nie pasc. Basiek zostawiam wszystko w twoich rekach. Nie
zawiedz nas!
7 sty 20:19
Basiek: Fajnie byłoby coś takiego dostać na maturze. 95% maturzystów by poległa
7 sty 20:19
ZKS:
To jeszcze dam jedno od siebie idę kreślić.
Zbadaj liczbę rozwiązań równania cos2x − cosx + m = 0 w zależności od parametru m ∊ ℛ.
7 sty 20:21
Basiek: Czeeekaj, ja tu biedzę się nad pierwszym !
7 sty 20:22
Basiek: To tak:
1 przyp.
m=3 x=1, x=3, x=−1
2 przyp.
m=1
x=1+√2
x=1−√2
x=1
3 przyp. m=2
ma 4 pierwiastki podwójne x=0, x=2 więc nie spełnia warunków zadania.
7 sty 20:25
Godzio: Udowodnij, że w trójkącie ABC symetralna boku BC przecina dwusieczną kąta BAC w punkcie B
leżącym na okręgu opisanym na trójkącie ABC.
Zadanie na około 1 h czasu, jak się wpadnie na pomysł to od razu mamy rozwiązanie
7 sty 20:31
Basiek: Odpadam.
7 sty 20:34
Basiek: Mogę zapytać, co mam zrobić z tym drugim zad. od
ZKS?
Dochodzę do delty ... i tam już potem zależność od m mi zaginęła
7 sty 20:36
ZKS:
Jak Ci m znika nie możliwe?
7 sty 20:50
Basiek: Nooo bowiem
2cos2−cosx+m−1=0
cosx=t
2t2−t+m−1=0
Δ=t2−8m+8
Tak, już zauważyłam, że bredziłam
czyli teraz
2 rozw. dla Δ>0
1 rozw dla Δ=0
0 rozw dla Δ<0
ale..., czyli co a=1 , b=0 , c= 8−8m
Δ=02−4(8−8m)= 32m+32
I to byłoby idiotyczne, bo wychodziłoby, że
2 rozw dla m>−1
1 rozw. dla m=−1
i 0 rozw dla m<−1
−−
7 sty 20:54
ZKS:
Jeżeli stosujesz podstawienie to musisz też pamiętać zbiór wartości cosx.
cosx = t ∊ <−1 ; 1>.
7 sty 20:59
ZKS:
Zadanie nie polega na użyciu tylko Δ. Tutaj trzeba pomyśleć jakie przypadki trzeba rozważać
dodatkowo.
7 sty 21:01
Basiek: Pamiętam... wiem.
Żeszty. Toż to są m−ki, ten y ... Masz cholerną rację.
Czyli m∊<−1,1>
stąd...
brak rozwiązań dla m<−1 i dla m>1
1 rozw dla m=−1
2 rozw dla m∊(−1,1>
7 sty 21:03
ZKS:
m ∊ ℛ nie do <−1 ; 1>! Podstawiając za cosx = t właśnie to t ∊ <−1 ; 1> nie m!
7 sty 21:08
ZKS:
Dobrze to po próbuj zrobić to zadanie jak coś wejdę później bo teraz idę już naprawdę kreślić.
7 sty 21:13
Basiek: Ja już tego nie robię. Zabij mnie, ale jestem na to za głupia. Pa , dzięki za wszystko
7 sty 21:15
Benek: Czy mógłby mi ktoś pomóc rozwiązać tę granicę?
limn→∞ = √3n + 2*4n + 5n
Z góry dziękuję.
7 sty 21:17
Basiek: Benek Obawiam się, że to nie ten temat, wybacz.
7 sty 21:19
kylo1303: Ale poki co nie dawajcie odpowiedzi. Dopiero co wrocilem wiec tak za pare minut siade i tez
sprobuje swoich sil.
7 sty 21:42
And I see a wall: Zrób to drugie, co?
CHCĘ wiedzieć, bo oszaleję.
7 sty 21:44
kylo1303: to z cosinusami?
7 sty 21:45
Basiek: Znaczy, ja chcę wiedzieć. Rób w każdym razie.
7 sty 21:45
Basiek: To samo
7 sty 21:45
gosq: 1) zbiorem rozwiązań nierówności f(x)>1 jest przedział (−∞,1) natomiast zbiorem rozwiazan
nierownosci f(x)<4 jest przedział (0,∞). Wiedząc że funkcja f jest funkcją liniową rozwiąż
nierówność: 2<f(x)<6
2) Wykaż że dla każdej funkcji f(x)=ax+b prawdziwa jest nierówność: 12 [f(x−1)+f(x+1)]=f(x)
3) Napisz wzór funkcji liniowej której wykres przechodzi przez punkt P=(−1,1) i jest: a)
równoległy b) prostopadły do wykresu funkcji y= 13 x+3
Rozwiąże mi ktoś takie zadania? Kompletnie ich nie rozumiem (tak samo jak całej f liniowej)
Zależy mi aby poznać jak moge rozwiązać podobne np. na kartkówce.
Byłabym bardzo wdzięczna.
7 sty 21:49
kylo1303: Moja odpowiedz do zadania "cos2x − cosx + m = 0"
| | 9 | |
Dla m∊<0, |
| ) 4 rozwiazania
|
| | 8 | |
Dla m∊<−2,0) 2 rozwiazania
Dla m<−2 0 rozwiazan.
Czyli podsumowujac:
| | 9 | |
0 rozwiazan dla: m∊(−∞,−2) u ( |
| ,∞)
|
| | 8 | |
| | 9 | |
2 rozwiazania dla m∊<−2,0) u { |
| }
|
| | 8 | |
| | 9 | |
4 rozwiazania dla m∊<0, |
| ) |
| | 8 | |
7 sty 22:09
Basiek: Wygląda mądrze
7 sty 22:12
kylo1303: Dzieki, ale pytanie ile w tym prawdy xD
7 sty 22:12
kylo1303: Za jakies 15min wezme sie za to wczesniejsze od ZKS
7 sty 22:13
Basiek: Stawiam na 100%
7 sty 22:13
Basiek: Możemy
krzyczeć, żeby pojawił się ktoś
kompetentny. Co Ty na to ?
7 sty 22:15
kylo1303: Nie lubie krzyczec xD Poza tym moga nie uslyszec
7 sty 22:19
Basiek: Oj tam, oj tam.
Dziewoja w opresji− POOOOOMOOOOOCY!
<nadobny krzyk Baśki>
7 sty 22:21
Basiek: O tempora, o mores!
Nikt człowiekowi już nie pomoże. Szkoda, że nie mogę użyć mojego prawdziwego głosu, od razu by
poskutkowało
7 sty 22:28
kylo1303: Jednak musze jeszcze wprowadzic mala poprawke do rozwiazania
zaraz napisze
7 sty 22:33
kylo1303: | | 9 | |
0 rozwiazan dla: m∊(−∞,−2) u ( |
| ,∞)
|
| | 8 | |
1 rozwiazanie dla m=−2
| | 9 | |
2 rozwiazania dla m∊(−2,0) u { |
| }
|
| | 8 | |
3 rozwiazania dla m=0
| | 9 | |
4 rozwiazania dla m∊(0, |
| ) |
| | 8 | |
7 sty 22:37
Godzio:
Zawsze możecie zrobić moje, a je sprawdzę, bo do
ZKS nie chce mi się robić, bo coś czuję
że można się zakopać
7 sty 22:38
Basiek: Idę po herbatę i się wypłakać xD
Potem zobaczę to Twoje.
i piszcie zadania na kolorowo, co?
7 sty 22:40
kylo1303: Mowa o tym zadaniu:
"Udowodnij, że w trójkącie ABC symetralna boku BC przecina dwusieczną kąta BAC w punkcie B
leżącym na okręgu opisanym na trójkącie ABC.
Zadanie na około 1 h czasu, jak się wpadnie na pomysł to od razu mamy rozwiązanie"
Na pierwszy rzut oka to nie pasuje mi tutaj podwojne oznaczenie "B"
7 sty 22:44
kylo1303: Moja odpowiedz do zadania ZKS:
Dla m=1
x1=1−√2
x2=1+√2
x3=1
7 sty 22:53
ZKS:
Tutaj właśnie jest taki ładny haczyk do mojego zadania ponieważ x ∊ R więc dla tych co
napisałeś że jest 2 i 4 rozwiązania tak naprawdę jest nieskończenie wiele bo funkcja cosx jest
okresowa.
Czyli jest 0 rozwiązań lub nieskończenie wiele.
7 sty 22:55
kylo1303: Aha, uznalem ze przypuscmy dla x=π+2kπ to jest jako jedno
No ale to by sie zgadzalo xD
7 sty 22:56
ZKS:
Trzeba zawsze zwracać uwagę na to.
Czyli jest tak jak napisałeś:
| | 9 | |
0 rozwiązań dla m ∊ (−∞ ; −2) ∪ ( |
| ; ∞) |
| | 8 | |
| | 9 | |
nieskończenie wiele dla m ∊ <−2 ; |
| >. |
| | 8 | |
7 sty 22:58
kylo1303: No tak, ogolnie po czesci wynikalo to z tego ze pisalem sobie "na luzie", mysle ze na maturze
bym to zauwazyl.
Bo przykladowo jak widzialem ze dla m=−2 to mam tylko x=kπ, to w glowie pojawial sie ten zapis
ale na papierze juz nie. Przez co tez nie pisalem ze k∊C i calej tej otoczki, przez co jakos
tak przegapilem. W sumei wyjdzie mi to na dobre bo teraz bede bardziej zwracal na to uwage
(juz i tak raz sie nacialem na cos podobnego, w 2/4 zadaniach w odpowiedzi nie dalem k∊C i
dostalem 4 mimo ze wszystko dobrze bylo). A to drugie okej?
7 sty 23:01
ZKS:
Powinny Ci wyjść że dla dwóch parametrów m mamy 3 różne pierwiastki rzeczywiste.
7 sty 23:06
Basiek: A mnie chociaż to jedno wyszło dobrze?
7 sty 23:09
kylo1303: A pytanie:
(x−1)2=0 to x=1 Ty to liczysz jako jeden jedyny pierwiastek, czy 2 jednakowe (jeden podwojny)?
7 sty 23:10
ZKS:
To są dwa jednakowe (podwójny).
Basiek to zadanie zrobiłaś dobrze.
7 sty 23:15
Basiek: pfff, wreszcie.
7 sty 23:15
kylo1303: Czyli odpowiedz jest ze niby m=1 v m=3 ?
7 sty 23:16
ZKS:
Dany jest wielomian W(x) = x4 + x3 − ax + b. Wiedząc że xo = 1 jest podwójnym pierwiastkiem
tego wielomianu znajdź resztę z dzielenia wielomianu W przez dwumian x + 1.
7 sty 23:17
ZKS:
Nie niby tylko dla m = 1 ∨ m = 3 mamy 3 różne pierwiastki.
7 sty 23:18
kylo1303: Dla m=3 mamy:
(x2−2x+1)(|x−1|−3+1)=0
(x−1)2(|x−1|−2)=0
x1=1
x2=1
x3=3
x4=−1
7 sty 23:23
ZKS:
Są trzy różne pierwiastki są więc jest dobrze.
7 sty 23:26
kylo1303: Ja ten przypadek odrzucilem jako ze sa 4 pierwiastki... Jest powiedziane "3 pierwiastki" to
maja byc 3 a nie 4. Nie przekonuje mnie ta odpowiedz.
A do wielomianu to W(x)=x4+x3−7x+5 W(−1)=12
7 sty 23:29
juu: wykaż że jeśli od iloczynu dwóch kolejnych liczb całkowitych odejmiemy trzykrotnosć mniejszej
z
nich to otrzymamy kwadrat liczby o jeden mniejszej od mniejszej z tych liczb pomniejszony o
jeden
7 sty 23:29
kylo1303: Zaloz oddzielny temat, zadanie wystarczy dobrze zapisac i powinno wszystko wyjsc.
7 sty 23:32
ZKS:
3
różne pierwiastki czyli jeden mógł mieć krotność nawet i 100 ale by były 3.
7 sty 23:32
ZKS:
A tego wielomianu jednak nie zrobicie.
7 sty 23:33
Basiek: Ups.
Z grubsza przysnęłam.
7 sty 23:40
kylo1303: A co niby jest zle z moim wielomianem? Nie przekonasz mnie ze polecenie jest dobrze
sprecyzowane. Tzn taka odpowiedz jest ok, ale spokojnie mozna sie tutaj z tym klocic.
7 sty 23:42
kylo1303: Nie wiem co jest nie tak z moja odpowiedzia ale wedlug mnie wszytsko sie zgadza.
W(x)=(x−1)2(x2+3x+5) (jakbys chcial inny zapis, po wymnozeniu da to samo)
7 sty 23:46
Basiek: Ja doszłam do postaci W(x)=(x−1)
2(x
2+3x+d)
Z tym, że nie mam zielonego pojęcia jak wyliczyć to d
7 sty 23:52
kylo1303: podziel dwa razy przez (x−1), reszty ma nie byc (ma byc rowna 0 ) to ci powinno wyjsc
7 sty 23:54
Basiek: Co mam Twoim zdaniem podzielić Kylo?
7 sty 23:55
ZKS:
Ale jak doszedłeś do tej postaci?
7 sty 23:55
ZKS:
A wyżej napisałeś okej.
7 sty 23:57
matematyka ;/: x3+5x2−x−5 podzielić przez x2+4x−5
jak to uprościć?
7 sty 23:57
Basiek: Dziecko drogie, OUT mi stąd, bo zrobię się niedobra!
7 sty 23:58
ZKS:
{x
2 + y
2 = 5
{log
2x + log
2y = 1
Rozwiązać układ równań.
Za chwilkę znajdę coś ciekawszego.
8 sty 00:00
matematyka ;/: spoko
/ thanks for help
8 sty 00:00
Godzio:
A moje zadanie robicie czy co ?
8 sty 00:01
Basiek: Cholera− GERUND nie INFINITIVE.
"Thanks for helpING" − jak chcemy błysnąć ironią i pokazać jakimi jesteśmy poliglotami, róbmy
to poprawnie!
8 sty 00:03
matematyka ;/: hahaha
8 sty 00:04
Basiek: Ja już nie robię NIC. Przechodzę załamanie nerwowe.
Ale Wam życzę powodzenia.
8 sty 00:06
Vax: Warto znać taką własność, że jeżeli x0 jest k−krotnym miejscem zerowym f(x) to fk−1(x0) =
0, u nas wiemy, że W(x) = x4+x3−ax+b i x0=1 jest 2−krotnym pierwiastkiem W(x), więc (W'(x)
= 4x3+3x2−a):
W'(1) = 0 ⇔ 4+3−a = 0 ⇔ a=7, czyli:
W(x) = x4+x3−7x+b, teraz znowu:
W(1) = 0 ⇔ 1+1−7+b = 0 ⇔ b = 5
Czyli W(x) = x4+x3−7x+5
8 sty 00:07
Basiek: Genialne w swej prostocie, Vax.
8 sty 00:09
ZKS:
8 sty 00:09
kylo1303: Wystarczylo podzielic Hornerem dwukrotnie przez x−1
W pierwsyzm wyjdzie ze b+2−a=0
w drugim natomiast 7−a=0
Z tego mamy a i b. Jest nawet krocej niz u Vaxa. Do tego ukladu to sie za chwile zabiore.
8 sty 00:12
ZKS:
Zrób zadanie które podał
Godzio.
8 sty 00:13
kylo1303: A poza tym srednio rozumiem ta wlasnosc xD
8 sty 00:14
ZKS:
Tutaj wykorzystujemy pochodne.
8 sty 00:18
kylo1303: Ten uklad prosty. Mnoze drugie przez 2, potem robie z x i y potegi, podstawiam pod jedno z
nich, korzystam z def. logarytmu i mam rownanie z 1 niewiadoma
8 sty 00:18
Basiek: A ja zrozumiałam, przesuwamy wszystko o jedną potęgę
A pierwiastek nadal jest pierwiastkiem
tego nowego wielomianu, tylko jednokrotnym
8 sty 00:19
kylo1303: (y2=1 x2=4) v (y2=4 x2=1) Nie chce mi sie tego rozpisywac
8 sty 00:21
kylo1303: No tak Basiek, to i ja zauwazylem. A skoro tak zrozumialas to moze powiesz dlaczego mozemy
tak zrobic ? xD
8 sty 00:22
Basiek: z założeniami, że
x>0
y>0
8 sty 00:22
Basiek: Dlatego możemy tak zrobić, że jest to własność, która wynika z pochodnych, którą byś znał,
gdyby nie okroili programu w LO?
8 sty 00:23
kylo1303: Zgadza sie, z takimi zalozeniami. A to zadanie od Godzio to chyba zostawie na jutro zeby
nie psuc sobie dobrej passy.
8 sty 00:24
kylo1303: I wszystko jasne ^^
8 sty 00:24
Basiek: Dzieci moje drogie, dzięki za wszystko dziś.
Dobranoc
8 sty 00:33
kylo1303: O kurde, to juz w pol do pierwszej jest
Mnie bedzie mozna zastac gdzies do 5tej pewnie, moze
rozrysuje sobie zadanie z trojkatem to mi pewnie pare godzin zleci.
8 sty 00:36
Basiek: Dopiero
8 sty 00:37
Joanna: Naszkicuj wykres funkcji (f) określonej w następujący sposób:
5 dla x< −4
x kwadrat + 2x−3 dla −4<x≤2
−x+7 dla 2<x≤5
a) dziedzina i przeciwdziedzina
b) wartość nax. i nim. funkcji
c) maksymalny przedział monotoniczności
d) czy funkcja jest różnowartościowa, uzasadnij
8 sty 00:38
Basiek: Będę krzyczeć.... mogę?
To powyżej wystarczy narysować− poziom 1LO. Powodzenia.
8 sty 00:40
Godzio: kylo dawaj moje robisz
zacznij nowy dzień z wielkim kopem
8 sty 00:42
Joanna: nikt mi nie pomoże z tym
8 sty 00:44
kylo1303: Poki co to sie "odstresowuje" (czyt. gram) ale potem moze siade
8 sty 00:53
Joanna: fajnie by było bo mam kolokwium z tego rano
8 sty 01:01
kylo1303: Ale czego nie umiesz? Narysowac? okreslic dzidziny?
8 sty 01:02
ZKS:
Znaleźć wszystkie n ∊ N dla których wielomian
W(x) = (x
3−5x+1)
n+(x
3 − 3x − 1)
n
| | 2 | |
daje przy dzieleniu przez (x−2) resztę |
| tg20otg40otg80o |
| | √3 | |
Godzio pamiętasz to zadanie?
8 sty 01:05
Joanna: danych do tego wykresu.. mój mózg dzisiaj już nie pracuje a od rana znowu szkoła
11h
8 sty 01:14
kylo1303: Czy ty
ZKS nie masz serca? o godzinie 1szej w nocy takie zadanie
8 sty 01:16
kylo1303: A ty Joanna nie pisz tutaj, masz swoj temat i tam reszte.
8 sty 01:16
Joanna: aha spoko..
8 sty 01:19
ZKS:
Kurde myślałem że to 11 jest.
8 sty 01:19
Godzio:
Coś mi się kojarzy
8 sty 01:46
ZKS:
Ale niestety nie chcą już tego robić.
8 sty 02:01
Godzio:
Takie fajne zadanka
8 sty 02:06
ZKS:
Nawet bardzo fajne.
Ja już się będę zbierał na spanie.
Dobranoc.
8 sty 02:16
Godzio: Dobranoc
8 sty 02:30
kylo1303: Twoje zadanie Godzio wymaga odpowiednich warunkow, w wiekszosc trojkatow to cos nie
zachodzi. Ogolnie moglbys poprawic zapis, bo tak samo uzyte jest "B" jako 2 rozne punkty.
8 sty 02:35
Basiek: Godzio? Jesteś?
8 sty 02:44
kylo1303: Odpowiedz do zadania ZKS:
Dla n parzystych.
8 sty 02:46
Godzio: Zadanie jest ok. gwarantuję
8 sty 03:57
Godzio: A czekaj
8 sty 03:59
Godzio: Udowodnij, że w trójkącie ABC symetralna boku BC przecina dwusieczną kąta BAC w punkcie F
leżącym na okręgu opisanym na trójkącie ABC.
Skopiowałem polecenie, a jak je robiłem to chyba zobaczyłem ten błąd i dałem takie oznaczenie,
więc niech tak będzie
8 sty 04:06
kylo1303: Ale ze niby to jest spelnione dla kazdego trojkata? Jesli sie nie myle (wniosek na podstawie
rysunkow w mojej wyobrazni) to trojakt musi byc rozwartokatny, bo w ostrokatnym punkt F bylby
wewnatrz trojkata...
8 sty 04:35
Vax: Zajdzie dla każdego
8 sty 13:17
Godzio:
8 sty 13:19
Basiek: Doszłam do wniosku, że potrzebne mi zmiany i motywacja.
Pewnie pojawię się za jakiś czas. Do zobaczenia.
8 sty 16:17
kylo1303:
Tak samo co by bylo z trojkatem rownoramiennym, gdzie dwusieczna pokrywa sie z wysokoscia i
symetralna? Moze chodzi o kolo a nie okrag? Albo ja czegos nie lapie w tym zadaniu.
8 sty 17:05
Godzio:
Jeśli chodzi o trójkąt równoramienny to warunek jest spełniony, jeśli zrobi się dokładnie
rysunek to zawsze wyjdzie, a to będzie zachodzi dla każdego i nie ma opcji że nie zachodzi
Więc nie szukaj kontrprzykładów tylko spróbuj to dowieść
9 sty 00:23
rumpek:
No witam wszystkich
a w szczególności
Godzia do którego piszę z interesem
Masz może jakieś zadania ze stereometrii, które mogą trafić się na maturce − takie praktyczne
(na liczbach − bo w większości takie były w ostatnich latach ) Takie z przekrojami itp.
Jakbyś miał takowe, to byłbym chętny
Oczywiście nie dzisiaj. Muszę zacząć przypominać sobie
stereometrię z gimnazjum
9 sty 00:30
Godzio:
Przypomnij się jutro koło 21, coś znajdę
9 sty 00:33
Godzio:
kylo to jak z tym zadaniem
?
9 sty 03:49
kylo1303: Poki co nijak, musze przysiasc i zrobic dobry rysunek bo na ten moment nie jestem przekonany
czy taki cos zachodzi w kazdym trojkacie xD Sprobuje dzisiaj to porobic, jesli nie wyjdzie to
dopiero w srode.
9 sty 10:13
AS: Kojarzysz mi się z Justyną Kowalczyk.
Wytrwała i zawsze do przodu.
9 sty 12:15
kylo1303: Godziu, z przykroscia informuje ze zadanie to najwczesniej w piatek. Jutro nie ma opcji
zebym znalazl czas, w czwartek tez ciezko bedzie. W piatek jesli gdzies sie wyjdzie to tez
odpadnie wiec zostanie weekend. Chyab ze na lekcjach zrobie, kwestia tego czy mi sie bedzie
chcialo xD Tak wiec cierpliwosci poki co.
10 sty 23:17
Godzio:
Czekam
Ale podzielam zdanie
ASA
11 sty 01:53
kylo1303:
Dzisiaj zrobilem malutki krok do przodu, mianowicie podczas lekcji wykonalem rysunek i
stwiedzilem ze takie cos zachodzi. Jako ze chce maksymalnie skrocic czas wykonywania zadania
(w ostatnim czasie mam male "urwanie glowy") chcialem zadac pytanie czy powinno sie to wykonac
tak jak mi sie wydaje:
Z punkt F rysuje odcinki do A i B, a nastepnie udowadniam ze ∡F+∡C=∡FAC+∡FBC=180 ?
Jesli takie cos zachodzi to wtedy na czworokatcie ABCF mozna opisac kolo, czyli pkt. F lezy na
okregu opisanym na trojkacie ABC.
Jesli nie o to tu chodzi to wolalbym zeby ktos mi napisal niz sam mialbym do tego dojsc po
straconej godzinie. Poki co zmiatam na zajecia dodatkowe, ale moze wiczorem przysiade do tego
(a na pewno zajrze czy ktos odpisal). Pozdro.
12 sty 14:57
kylo1303: Dodam jeszcze ze dla rownobocznego nie do konca zachodzi to "twierdzenie", ale tak na oko to i
dla 59 i 61 tez by pewnie nie zaszlo xD
12 sty 14:59
Anonimowy:
Dla równobocznego również zachodzi
Zauważ. że Ty korzystasz z tego co masz udowodnić, więc
nie tędy droga
12 sty 15:12
kylo1303: napisalem "nie do konca", bo w pewnym sensie one sie nie "przecinaja", aczkolwiek ten punkt F
zaawiera sie zarowno w symetralnej jak i dwusiecznej.
Jesli mialbym myslec nad innym sposobem to chyba musialbym kobinowac z promieniami cos, no w
kazdym badz razie sprobuje podejsc do tego od innej strony. Ale ta przyjemnosc zostawie sobie
na jutro.
12 sty 18:05
Godzio:
Czekam, czekam i czekam i nic
14 sty 03:13
kylo1303: Wczoraj w domu bylem tylko pomiedzy powrotem ze szkoly a wyjsciem do kina, czyli miedzy 14−18.
Nie bylo czasu. Dzisiaj pobudka o 15, zaraz znowu wychodze wiec zadanka bede robil wieczorem/w
nocy. Tylko tam nie nastawiaj sie na nie−wiadomo−co, bo jak nie wyjdzie w jakies 30min to dam
sobie spokoj bo dzisiaj chcialem dalej robic zestawy z Aksjomatu.
14 sty 17:27
mmm: {3√4}log4√2 32
Ktoś chętny do rozwiązania?
14 sty 17:46
mmm: {3√4}log4√2 32
Ktoś chętny do rozwiązania?
14 sty 17:47
mmm: {3√4}log4√2 32
Ktoś chętny do rozwiązania?
14 sty 17:50
Eta:
(4√2)2=32 to: log4√232= 2
(3√4)2=3√16= 3√8*2= 23√2
14 sty 17:51
%25253Cb%25253Emmm%25253A%25253C%25252Fb%25253E%252520%25257B%25253Csup%252520class%25253D%252522p2%252522%25253E3%25253C%25252Fsup%25253E%25253Cspan%252520class%25253D%252522p3%252522%25253E%2525E2%252588%25259A%25253C%25252Fspan%25253E%25253Cspan%252520class%25253D%252522p4%252522%25253E4%25253C%25252Fspan%25253E%25257D%25253Csup%25253Elog%25253Csub%25253E4%2525E2%252588%25259A2%25253C%25252Fsub%25253E%25252032%25253C%25252Fsup%25253E%25250A%25250AKto%2525C5%25259B%252520ch%2525C4%252599tny%252520do%252520rozwi%2525C4%252585zania%25253F%25250A%25250A
14 sty 17:51
mmm: sorki za spam ale myślałem że się nie wysłało
14 sty 17:55
Eta:
14 sty 17:57
mmm: dzięki ETA, mi innym sposobem wyszło tak samo,więc teraz mam pewność że jest dobrze
14 sty 18:01
kylo1303: Czy ktoś moglby mi dac rade do zadan z tematu "plaszczyzny i proste w przestrzeni" ? Bo dla
mnie to jakas apstrakcja....
Przyklad zadania:
Odcinek AB długosci a lezy na plaszczyznie π. Odcinek AC jest prostopadly do plaszczyzny π.
| | π | |
Odcinek BD tworzy z plaszczyzna kat o mierze |
| i jest prostopadly do odcinka AB. Ponadto |
| | 6 | |
|AC|=|BD|=b. Oblicz dlugosc odcinka CD.
15 sty 19:08
Basiek: Hm, a coś takiego jest na maturze w ogóle?
15 sty 19:09
Eta:
"a
bstrakcja" ! ......... I co z maturą z j.polskiego?
15 sty 19:14
Basiek: Eta ludzie nie lubią, jak się ich poprawia.
A co by miało być z maturą z polskiego?
15 sty 19:15
kylo1303: Ja lubie, mnie mozesz poprawiac do woli i przyjme to z godnoscia. Moj problem polega na tym ze
na komputerze inaczej sie pisze niz na papierze, piszac recznie nie zrobilbym wielu bledow
ktore robie piszac na klawiaturze (ale mimo wszystko nie popelniam takich bledow jak "z kont"
albo "wogle" )
Nie wiem czy sa, robie rysunek, powstaje czworoscian, 2 boki maja dlugosc b, jeden a oraz dwa
boki maja √a2+b2. Odpowiedz zze CD tez ma √a2+b2, ale ja jakos nie widze zeby to bylo
rownoramienne.
15 sty 19:20
kylo1303: A z matura z polskiego to ma byc 30% i wystarczy xD A tyle to spokojnie bede mial (taka mam
przynajmniej nadzieje)
15 sty 19:21
Basiek: Kylo motywujesz mnie do "nicnierobienia", to przykre.
15 sty 19:34
ktoss: Ja dorzucę od siebie kombinatorykę (rozszerzenie)
Ile liczb trzycyfrowych parzystych a ile czterocyfrowych podzielnych przez 5 można ułożyć z
cyfr: 0,1,2,4,7,8,9
15 sty 19:35
Basiek: czterocyfrowych podzielnych przez 5 : 294
trzycyfrowych parzystych: 168
?
15 sty 19:37
ktoss: A skąd to wzięłaś? Bo ja się zastanawiam, jak to zadanie zrobić
15 sty 19:39
Basiek: Czterocyfrowe bla blaaa
_
na pierwszym miejscu może być 6 liczb (0 odpada)
na drugim 7 liczb (wszystkie)
na trzecim 7 liczb (tak samo)
a na czwartym może być 5 lub 0 −> 5tki nie mamy, więc MUSI być 0, nie mamy wyboru więc−> 1
możliwość.
Wszystkie możliwości mnożymy 6*7*7*1 =....
15 sty 19:41
kylo1303: Czterocyfrowe podzielne przez 5 musza miec 0 na koncu, pozostale cyfry dowolnie. W
trzycyfrowych ostatnia musi byc parzysta a pierwsza nie moze byc 0.
15 sty 19:41
Basiek: Drugie podobnym schematem
15 sty 19:43
kylo1303: Tzn tam mala poprwka: w czterocyfrowych tez oczywiscie 0 nei moze byc na poczatku (to chyba
oczywiste). Ale z takimi zadanimi to rob wlasne tematy bo to nie jest dobre miejsce.
15 sty 19:44
ktoss: Kurde, ale skąd bierzesz te na drugim 7, na trzecim 7
15 sty 19:45
Basiek: Na drugim miejscu możesz mieć 0,1,2,4,7,8 LUB 9 −> 7 możliwości.
7 liczb... itd łapiesz?
15 sty 19:45
ktoss: Nie bardzo
Nawet nie wiem, po co na rozszerzenie szedłem...
A w tym jak będzie?
Ile liczb czterocyfrowych parzystych a ile trzycyfrowych podzielnych przez 5 można zapisać z
cyfr: 0,2,4,5,6,8,9
15 sty 19:49
ktoss: 6*7*2
15 sty 19:50
Basiek: Ile liczb czterocyfrowych parzystych a ile trzycyfrowych podzielnych przez 5 ...
6*7*7*5
15 sty 20:04
kylo1303: Trzycyfrowe zapisales dobrze. Parzyste czterocyfrowe napisala Basiek.
Powtarzam: tutaj nie jest kolko wyrownawcze tylko zadania dodatkowe dla maturzystow. Zrob
oddzielny temat.
15 sty 20:07
Basiek: W zasadzie miałam powtórkę przed jutrzejszą matmą
Ale fakt, nie ten temat
Żegnaj Ktosiu
15 sty 20:10
kylo1303: Jeszcze jakby te zadania byly na poziomie rozszerzonym... Ale nie sa one zbyt wymagajace wiec
uwazam ze to takie zasmiecanie tematu, rownie dobrze 100 innych osob mogloby pisac tutaj swoje
zadania.
Zrobilem juz 3 z 4 zadan wiec uwazam ze robie postepy, ale jeszcze jedno najgorsze.
Basiek Zaczeliscie juz stereometrie?
15 sty 20:16
Basiek: Co Ty. My dalej prawdopodobieństwo, potem dopiero statystyka, a dopiero na sam koniec
stereometria
15 sty 20:17
kylo1303: No to troche przed wami, statystyka jest do doopy, zero myslenia tylko liczenie na brzydkich
liczbach. Myslalem ze moze zdolasz pomoc, ale sam juz wszystko zrobilem. Ciekawe kiedy jakies
nowe zadanka tutaj dadza, tylko byleby nie byly z planimetrii.
15 sty 20:27
Basiek: Od kilku dni nie robię nic.
Nie mam ochoty, ani weny. Chyba potrzebne mi ferie.
A ze
stereometrii to jestem totalna noga. W gimnazjum zrobiliśmy najprostsze graniastosłupy ... a
od tego czasu NIC ze stereometrii. Nawet z podstawą mam problem
15 sty 20:29
kylo1303: No bo taki jest program nauczania w liceum, stereometria jest chyba ostatnim dzialem w 3ciej
klasie, wczesniej to tylko planimetrie i g. analityczna ktore stanowia fundamenty g.
przestrzennej.
15 sty 20:31
kylo1303: No i
1300 wedruje do mnie
15 sty 20:31
Eta:
z ΔABD |AD|
2= a
2+b
2 ⇒ |AD|=
√a2+b2
| | b | |
z ΔBED x= |
| to ΔADC jest równoramienny |AD|= |CD| |
| | 2 | |
zatem |CD|=
√a2+b2
15 sty 20:33
Basiek: Hm, analityczna już była, planimetria w 2giej klasie... , g. analityczna, kombinatoryka z
prawdopodobieństwem, statystyka i stereometria, tak to wygląda u nas
15 sty 20:33
kylo1303: Dziekuje
Eta ale jak pisalem wyzej poradzilem sobie z tym zadaniem
15 sty 20:41
kylo1303: btw. twoje rysunki zawsze sa takie przejrzyste xD Po prostu mialem problem z "przelaczeniem"
mozgu na myslenie przestrzenne.
15 sty 20:43
Basiek: Twoje
Lubię poprawiać innych.
15 sty 20:50
Eta:
Złośliwość.......... to przeważnie cecha kobiet
15 sty 21:06
Problematyczny: To nie jest list żeby pisać twoje wielką literą
15 sty 21:12
kylo1303: Dokladnie. Tak samo moglbym czepiac sie "ą" i "ę" oraz innych bledow wszelakiego rodzaju. Tylko
ze nie w tym rzecz
Jesli chodzi o "szacunek" do adresata to uwazam ze wytluszczanie nicku w
zupelnosci wystarcza.
15 sty 21:17
Basiek: Mogę być złośliwa, to dobra cecha.
Nie list, a forum, tu zwracasz się bezpośrednio do adresata, stąd zwroty "Wy" , "Ty" w mailach,
sms−ach oraz przemówieniach, a także na forum należy pisać z dużej litery.
Pozdrawiam !
15 sty 21:17
Problematyczny: Nie z dużej, tylko wielką!
Normalnie czuję się jak moja nauczycielka polskiego z gimnazjum
15 sty 21:19
Basiek: "Jedni wolą pisać dużą literą, inni wielką literą – to kwestia wyłącznie upodobań, żadnych
zakazów ani nakazów tu nie ma. Trzeba tylko pamiętać, aby nie pisać z dużej (wielkiej) litery,
gdyż wyrażenia te mają złą opinię w wydawnictwach poprawnościowych, mimo że ich frekwencja w
tekstach jest duża. Ciekawe, że wydawnictwa normatywne akceptują rzadko spotykany wariant od
dużej (wielkiej) litery. Zazwyczaj wyrażenie to spotykamy w innej funkcji, np. „Od dużej
litery E w nazwie pochodzi właśnie nazwa serii: Big – E” (CKM).
— Mirosław Bańko"
Będę teraz pisać poprawnie. Dużą literą
. Dziękuję.
15 sty 21:24
kylo1303: To jest z pewnego pisemka dla facetow? xD
15 sty 21:26
Basiek: Proszę?
15 sty 21:27
kylo1303: Skrot CKM ma kilka rozwiniec.
15 sty 21:34
Basiek: I oto masz, pierwsze skojarzenie faceta.
Thanks God, I'm a woman.
15 sty 21:37
kylo1303: Wrzuc w google to sie przekonasz co jest bardziej popularne pod tym tagiem.
15 sty 21:38
Problematyczny: Czyżby ciężki karabin maszynowy?
15 sty 21:40
Basiek: Wrzuciłam. Pierwsza strona mnie oświeciła szybko i skutecznie. Nawet nie musiałam czytać,
wystarczyły obrazki.
15 sty 21:42
kylo1303: No widzisz, wiec akurat moje skojarzenie bylo jak najbardziej na miejscu, powiedzialbym ze
nawet duzo bardziej niz twoje.
15 sty 21:53
Basiek: Jasne.
Twoje.
15 sty 21:56
kylo1303: a ja bede pisal twoje z malej
mozesz sie odwdzieczyc tym samym.
15 sty 22:03
Basiek: Nie, mój poziom kultury osobistej mi na to nie pozwala.
15 sty 22:04
kylo1303: Nie odnosilbym sie tutaj do kultury osobistej, bo akurat tej mi nie brakuje. Moglbym dodac to
na liste "glupot wymyslonych przez ludzi". To ze sobie niektorzy powymyslali pewne kanony
zachowan nie oznacza ze wszyscy musza ich przestrzegac. Rozumiem ze sa pewne normy moralne i
obyczajowe, ktorych nie nalezy lamac, ale tego bym tutaj nie zaliczyl. Jesli pisalbym list
formalny, czy nawet maila lub smsa do osoby starszej lub zwiazanej ze mna tylko relacjami
"sluzbowymi", wtedy oczywiscie pisalbym wielka litera. A jako ze pisze do
"kolegow−rowiesnikow" moge pozwolic sobie na styl nieformalny, ktory nie wymaga ode mnie
zaczynania zdania wielka litera i konczenia kropka, tak jak i uzywania znakow polskich ze
znakami diakrytycznymi itp.
15 sty 22:16
Basiek: Boże, żartowałam. Spokojnie.
15 sty 22:22
Basiek: Chciałam się tylko podrażnić, nie musisz mnie zjadać na śniadanie i uważać za idiotkę o
dziwacznych przekonaniach, która sądzi, że ma rację, mimo że jej nie ma.
15 sty 22:23
15 sty 22:23
Tragos: oo
ciekawie widzę się tu zrobiło
15 sty 22:24
kylo1303: Musze sciagnac od ciebie tekst: "Spokojnie
"
Te moje mini wywody nie mialy na celu nikogo obrazac, wyrazilem tylko swoje poglady na ten
temat i
wytlumaczylem dlaczego nie bede pisal zaimkow z wielkiej litery xD Nie bylo w tym ani troche
agresji, irytacji, ani zadnej innej negatywnej emocji.
15 sty 22:25
Basiek: Jaaasne, spokojny. Po pierwszych dwóch zdaniach stwierdziłam, że nie będę czytać tej
patetycznej odezwy, bo nie zostawisz na mnie suchej nitki.
Tragos− pojęcie względne.
15 sty 22:26
kylo1303: A co do drugiego zdania i "listy glupot wymyslonych przez ludzi" to po prostu uwazam ze sa
pewne kultywowane zwyczaje, ktore w mojej opinii sa bezsensowne. Do takich naleza wszytskie
czysto komercyjne swieta (typu walentynki) i wiele innych.
15 sty 22:28
Basiek: Mhm, mhm. Mów do mnie jeszcze
15 sty 22:30
kylo1303: Juz skonczylem, ale moze zalapiesz sie kiedys na moj inny wyklad.
15 sty 22:32
Basiek: Poproszę. Masz może w repertuarze coś wesołego?
15 sty 22:33
kylo1303: Bajki i legendy z happy endem?
15 sty 22:33
Basiek: Następny w kiepskim humorze?
A co do historii, to najlepiej, jeśli ktoś ginie. Wszyscy.
15 sty 22:34
kylo1303: oO A mialo byc cos wesolego. A humor jest jak najbardziej w porzadku. Powiem nawet
ze jestem z siebie zadowolony bo wszystkie zadanka mi wyszly, mimo ze na poczatku myslalem ze
to totalna abstrakcja i nie potrafilem zrobic rysunku. Zebys wczoraj (dzisiaj do godizny
3 rano) byla, wtedy walczylem z zadaniem od Godzio i ta walke przegralem.
15 sty 22:41
15 sty 22:43
Godzio:
15 sty 22:48
kylo1303: Nie do konca. Jestem osoba ze nawet jak mam zly humor to nie odbija sie to na innych.
"Jestem spokojny i opanowany", a ze czasami mozna mylic zarty z jakimis docinkami to nie moja
wina (w sumie to moja). Ale zadania maja wplyw na moj chwilowy nastroj. Ale tutaj to tez
trzebaby sie rozpisywac, bo samo to ze nie umiem zadania to zaden problem, gorzej jak sie
mecze dluzszy czas a potem zauwazam idiotyczny blad przez co wszystko co dalej robilem bylo
bledne. Wtedy sie wkurzam (ale tak wewnetrznie) xD
15 sty 22:49
kylo1303: Godzio a ty sie tutaj nie wtracaj ze swoimi lapami xD Poza tym przypominam ze obowiazuje
meska solidarnosc
15 sty 22:50
15 sty 22:51
Godzio:
Ok, nic nie piszę już
Też byłem wkurzony jak mi zadanie nie wyszło które robiłem tydzień po
około 3 h dziennie
15 sty 22:52
Basiek: Boże... z kim ja się zadaję.
To straszne.
Swoją drogą− kwejk krzyczy, że muszę w ten weekend dotknąć matematyki, życie jest okrutne.
15 sty 22:53
Godzio: Jak mnie lubicie to pamiętajcie ! Wtorek, godzina 15:15 trzymajcie kciuki
Zaczynam pisać
kolokwium z analizy
15 sty 22:54
Basiek: Będziemy, a każdy ma aż 2 kciuki!
15 sty 22:56
ZKS:
Godzio przetestowałem Battlefield 3 i musze powiedzieć że naprawdę fajoweee.
15 sty 22:57
Eta:
15 sty 22:57
Godzio:
No to git
Eta będziesz koło północy ?
15 sty 22:57
ZKS:
Więc będę musiał zacząć oszczędzać.
15 sty 23:04
Godzio:
Koło 100 chyba kosztuje nie ? Dostałem na urodzinki
, więc nie za bardzo się orientuje
15 sty 23:06
ZKS:
Właśnie chyba coś koło 100 może troszkę ponad ale właśnie się zastanawiałem czy sobie nie kupić
samego kodu za 50 zł.
15 sty 23:15
Basiek: Z ekonomicznego punktu widzenia.. kup kod
15 sty 23:57
Ola: Prosiłabym o pomoc w zadaniu:
Podana funkcja: y= 2x+3−2
1) Wyznacz dziedzinę i zbiór wartości funkcji. 2) Podać równanie asymptot. 3) Oblicz miejsce
zerowe. 4) Określić monotoniczność. 5) Podaj przedziały, w których funkcja przyjmuje wart.
dodatnie i ujemne.
Proszę chociaż o wskazówki, co zrobić na początku z tą funkcją. To funkcja liniowa, więc
powinna mieć równanie y=ax+b, nie wiem jak ją przekształcić. Każda odpowiedź będzie dla mnie
pomocą. Dziękuję z góry!
16 sty 00:08
Ola: źle się skopiowało, przepraszam chodziło o funkcję:
y=2x+3−2
16 sty 00:16
Basiek: Źle trafiłaś, nie ten temat, nie to miejsce, przykro mi
16 sty 00:17
Eta:
Porządek musi być
16 sty 00:21
Godzio: Eta mam dla Ciebie zagadkę
16 sty 00:22
Eta:
Hehe
jaką?
16 sty 00:23
Godzio:
Karkówki są max na 1 pkt, koło na 25
16 sty 00:24
Eta:
Zagadki dla mnie ma często moja "połówka"
16 sty 00:24
Eta:
Łatwa zagadka
suma cyfr
27
16 sty 00:28
16 sty 00:33
Godzio:
Hmmm, ale w sumie to kilka ma sumę równą 27
16 sty 00:37
Eta:
Hehe
.......... dzięki TOBIE ! Gratulacje
16 sty 00:37
Godzio: ok
16 sty 00:44
Godzio: Oj dobrze, że trafiłem na to forum
16 sty 00:49
Eta:
Zmów zdrowaśki za
Jakuba i nie tylko
16 sty 01:08
kylo1303: Godzio Wstyd, jakis twoj kolega napisalem lepiej od ciebie xD
16 sty 01:09
Eta:
Pora spać
Dobranoc
16 sty 01:29
Godzio: Aj tam
, Dobranoc
16 sty 01:57
kylo1303: Dobranoc, Tez juz zmykam.
16 sty 02:07
Basiek: Odświeżam
Może jakieś 2 zadanka z Aksjomatu na poprawę humoru?
16 sty 18:52
kylo1303: Jakis konkretny dzial?
16 sty 19:13
Basiek: Już dostałam
5 zestaw− zad. 10
17 zestaw− zad.2
16 sty 19:17
kylo1303: To pierwsze juz bylo robione, chyba nawet w tym watku.
16 sty 19:19
Basiek: Może i robiłeś... ja nie, nawet chyba w tym czasie na to nie patrzyłam
Cóż... może zacznę?
16 sty 19:22
kylo1303: Powodzenia
I to akurat nie ja robilem tylko ktorys ze studentow. Ale moze cos mi sie myli.
16 sty 19:23
Basiek: Nie wiem, przeżywam kryzys wieku średniego.
16 sty 19:40
kylo1303: Czego nie wiesz?
16 sty 19:41
Basiek: Nic.
To nic nie odnosi się póki co do zadania, ponieważ najpierw musiałabym je przeczytać.
Swoją drogą− wytłumaczysz mi potem/ jutro/ przed piątkiem kilka rzeczy z kombinatoryki? Będę
całować ziemię, po której stąpasz.
16 sty 19:42
agusz: w ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość 30 cm i tworzy z wysokością
ostrosłupa kąt o mierze 45 stopni. Oblicz objętość tego ostrosłupa.
pomożecie?
16 sty 19:44
Basiek: Agusz nie to miejsce, nie ten czas. Przykro mi. Porządek musi być.
16 sty 19:45
agusz: jestem zdesperowana
16 sty 19:46
kylo1303: Przeciez to banal... masz w podstawie kwadrat. Rysujesz wysokosc (opada na punkt przeciecia
przekatnych w kwadracie). Laczysz z krawedzia boczna i masz rownoramienny prostokatny...
16 sty 19:51
Basiek: Dla Ciebie wszystko jest banałem... czasem mam ochotę zrobić Ci krzywdę
16 sty 19:54
kylo1303: Nie wszystko, geometria to czarna magia. Ale chyba nie powiesz ze to zadanie z gimnazjum
stanowi dla Ciebie problem? Z kombinatoryki moge probowac pomoc, ale mysle ze sporo
lepszych kandydatow sie znajdzie. Nie uwazam zebym w 100% ja opanowal, ale z checia pomoge to
sam sie czegos naucze.
16 sty 20:00
Basiek: Nie, chyba nie stanowi. Aczkolwiek stereometrii nie dotykam nawet patykiem
I hm, dzięki
Za jakiś czas się zgłoszę.
16 sty 20:01
agusz: dzięki za uświadomienie, coś mi sie pogmerało i w podstawie rysowałam trójkąt <załamka> teraz
to rzeczywiście bez problemu
dzięki
P.S matma to mega udręczenie..
16 sty 20:06
ZKS:
Dla jakich wartości parametrów a jeden z pierwiastków równania jest większy od 1 a drugi
mniejszy od 1.
(2a + 1)x2 − ax + a − 2 = 0
16 sty 21:01
Basiek: Hm, odnośnie zad. 10/ zestaw V...
x
3+ax
2−75=0
przekształciłam trochę tak...
x
2(x+a)=75
i stąd widać wyraźnie, że dla x∊N+ i a∊C
x
2=25 => x=5
x+a= 3 => a=−2
to by się zgadzało... zadanie BANALNE, aczkolwiek rozpisanie chyba raczej kiepskie.
16 sty 21:11
Basiek: UP
16 sty 21:24
ZKS:
tylko trzeba właśnie wpaść na tak banalne rozwiązanie.
16 sty 21:30
Basiek: aha... czad.
16 sty 21:32
ZKS:
Widzę że umiejętności rosną tak trzymaj.
16 sty 21:38
Basiek: Im więcej "nicnierobienia", tym jest lepiej. Mogę być dumna
16 sty 21:39
Basiek: A mogę jedno z Aksjomatu, którego hm, nie umiem ani trochę?
16 sty 21:42
ZKS:
O 21 : 01 napisałem zadanie.
16 sty 21:44
Basiek: Oj, tamtego nie zrobię chyba w tym tygodniu. Ale obiecuję zapisać sobie i ładnie pomyśleć nad
tym, tylko nie dziś (spr z fizyki!− czyli czarna magia, kurs zaawansowany)
Zad. Dany jest zbiór funkcji
f: {1,2,3}→{1,2,3,4,5}
Oblicz prawdop., że wylosowana funkcja będzie różnowartościowa.
I mnie za nic nie wychodzi dobry wynik...
16 sty 21:46
Tragos: 1400!
16 sty 21:48
Basiek: Tragos brawo, nawet nie zauwazyłam
I mam tak
Ω= 5
3= 125
A= 4*4*4=4
3= 64
P(A)=64/125
Czyli bzdurny wynik.
16 sty 21:52
ZKS:
A czemu moc zbioru a jest 43? Przecież ma być różnowartościowa.
16 sty 21:54
Basiek: toteż właśnie... obawiam się, ze nie do końca rozumiem zapis i treść, bo widzę coś takiego
chyba pierwszy raz na oczy.
stwierdziłam, że f. będzie różnowartościowa, gdy 1 przekształci w 2, 3,4 lub 5 (2 opcje)
2 przekształci w 1,3,4,5.... −> 4 opcje
i to samo z 3−jką
Oświecisz mnie?
16 sty 21:56
kylo1303: ZKS Czy w twoim zadaniu pojawia sie tylko "1" (czy moze jest " wieksze od 1 i mneijsze od
−1"?) Jesli tak, to czy wynik to a∊∅ ? Troche glupi, ale coz zrobic.
16 sty 22:00
ZKS:
Dla y = 1 możemy mieć na początku 5 opcji (wszystkie cyfry ze zbioru x)
następnie dla y = 2 jedna cyfra nam odpada ze względu na różnowartościowość czyli mam 4 opcje
na końcu dla y = 3 już dwie cyfry nam odpadły więc mamy 3 opcje.
Z reguły mnożenia otrzymujemy 5 * 4 * 3.
16 sty 22:04
ZKS:
kylo1303 pojawia się tylko 1 i odpowiedź nie jest że a ∊ ∅.
16 sty 22:07
Basiek: Aaaa, takie buty. Już jasne. Dziękuję, chociaż nadal nie do końca rozumiem ten zapis:
f: {1,2,3}→{1,2,3,4,5}
Być może google mnie uświadomią
16 sty 22:07
kylo1303: Meine błęden
przyjalem ze x
w=1 xD zaraz poprawiam
16 sty 22:10
kylo1303: Meine błęden
przyjalem ze x
w=1 xD zaraz poprawiam
16 sty 22:11
Basiek: To ja jeszcze raz:
http://pl.wikipedia.org/wiki/Zbi%C3%B3r_z_wyr%C3%B3%C5%BCnionym_punktem
X→Y
czyli to są jakby punkty?
(1,1) (2,1) (3,1)
(1,2) (2,2) (3,2)
(1,3) (2,3) (3,3)
(1,4) (2,4) (3,4)
(1,5) (2,5) (3,5)
domyślam się, ze odrzucamy te punkty (2,2) i (3,3)i jeszcze jakiś punkt z trójką...(który?!)
Albo wszystko sobie ubzdurałam (też możliwe)
16 sty 22:15
kylo1303: Odpowiedz druga:
| | 1 | | 6−2√23 | |
a∊(a1, |
| ) gdzie a1= |
| |
| | 2 | | 7 | |
16 sty 22:21
ZKS:
kylo1303 nie.
16 sty 22:25
kylo1303: zzzzzz
To moze podam warunki:
a≠0
Δ>0
f(1)<0
To nie wystarcza?
16 sty 22:28
ZKS:
To trzeba rozbić na przypadki.
dla a > 0
f(1) < 0
dla a < 0
f(1) > 0.
16 sty 22:31
kylo1303: Heh, myslalem o tym ale jakos tak doszedlem do wniosku ze to bez znaczenia xD
16 sty 22:33
ZKS:
Basiek ja tam głupotę napisałem
dla x = 1 i ze zbioru y mamy 5 opcji dla x = 2 mamy 4 opcje dla x = 3 mamy 3 opcje.
Funkcja jest różnowartościowa kiedy x1 ≠ x2 ∧ f(x1) ≠ f(x2).
Czyli jeżeli masz x = 1 i wartość równa 5 to dla x = 2 wartość już nie może przyjąć wartości 5.
16 sty 22:34
kylo1303: Czyli wychodziloby na to ze zamknie mi sie ladnie z drugiej strony
16 sty 22:36
Basiek: No widzisz... trzeba było tak od razu. Lampka się zaświeciła. Prochy na ból głowy, 2 kawy i ...
postanowilam zostać specjalistką od optyki !
16 sty 22:37
kylo1303: Ja juz bede szedl spac bo po 4h snu mam luki w mysleniu i trzeba odespac. Tak teraz sie
zastanawiam jak ja doszedlem do tego ze nie ma znaczenia czy a>0 czy <0 podczas gdy uznalem ze
f(1)<0 ...
16 sty 22:39
ZKS:
kylo1303 właśnie taka jest odpowiedź jaką napisałeś. Basiek przepraszam za
zamieszanie nie wiem co mi się ubzdurało tam że tak napisałem.
16 sty 22:42
kylo1303: Plusem jest to ze w kazdej z blednych odpowiedzi domyslalem sie ze cos jest nie tak xD (super
poccieszenie)
16 sty 22:44
ZKS:
Ale jakieś zawsze pocieszenie.
16 sty 22:49
Basiek: ZKS Weź, zgłupiałeś
? Nie przepraszaj. Jesteś pomocny, jak rzadko kto
za każdą pomoc
jestem naprawdę wdzięczna
Inaczej na to nie patrz
16 sty 23:00
Godzio:
Zadanka bez Godzia ! No ładnie
16 sty 23:01
Basiek: Skandal!
O tempora, o mores!
16 sty 23:02
ZKS:
Jak tam kolokwium
Godzio?
16 sty 23:02
Eta:
No właśnie
Godzio jak poszło?
16 sty 23:04
Godzio: We wtorek za dokładnie: 16 h
Ale wiesz co, to kolokwium nie ma większego znaczenia, równie dobrze mogę go napisać na zero =
nie pójść na nie
muszę zaliczyć ćwiczenia, a to już mam bo uzbierałem wystarczającą ilość
pkt
Najważniejszy jest egzamin
16 sty 23:05
Godzio:
Jutro o 21:20 zdam relacje
16 sty 23:05
Eta:
ok
16 sty 23:06
ZKS:
A egzamin kiedy piszesz?
16 sty 23:07
Godzio: 30.01
16 sty 23:09
Basiek: Powodzenia z egzaminami
Dziękuję za wszystko i dobranoc
16 sty 23:11
Godzio: Nic nie pomogłem, ale spoko (nie ma sprawy
)
16 sty 23:14
ZKS:
Dobranoc.
Najpierw trzeba życzyć powodzenia na kolokwium.
16 sty 23:14
Basiek: Znów odświeżam
Może jakieś 3 pocieszne zadania z Aksjomatu? Wystarczą numerki zestawu i zadanka
17 sty 21:24
kylo1303: Jesli masz dostep do zbioru to czego sobie losowo nie wybierzesz?
17 sty 21:29
Godzio: A to czemu ich sama nie robisz i wątpliwości nie rozwiewasz tutaj
?
17 sty 21:29
Basiek: Bo moje losowo wygląda:
"To trudne... zrobię kiedy indziej, tu jest dużo liczenia... to też odpada, o − to będę umieć!"
"LOSOWO"
17 sty 21:33
kylo1303: Ja ostatnio sie troche musialem pomeczyc z zadaniem 9 z zestawu 13
Nie jest trudne ale jak
chcialem wymnozyc i rozwiazac cos takiego:
(x−a)(x−a−r)(x−a−2r)(x−a−3r)=x
4−10x
2+m
To dalem sobie spokoj, pozniej oczywiscie doszedlem co i jak xD
17 sty 21:34
Basiek: Ekhem... wygląda milusio. To nie jest czasem ciąg arytmetyczny po lewej?
17 sty 21:36
Godzio: Napiszcie mi treść bo pożyczyłem mojemu uczniowi zbiór
17 sty 21:38
kylo1303: Tzn to ja to utrudnilem sporo.
Dane jest rownanie x4−10x2+m=0 wyznacz te wartosci parametru m, dla ktorych rownanie to ma
cztery pierwiastki, z ktorych mozna utworzyc ciag arytmetyczny.
17 sty 21:40
Basiek: Zapętliłam się. Zrobienie tego tabelką Hornera chyba nie było genialnym pomysłem
17 sty 21:52
DZIADZIA: basiek problem
17 sty 21:53
Basiek: Problemy są zawsze. Jaki?
17 sty 21:53
Mila: Wydaje mi się, że to już było i zostało ładnie rozwiązane!
17 sty 21:57
DZIADZIA: jeżeli sinus kata ostrego α wynosi 25,to wartosc wyrażenia √21/cosα jest rowna
A5/21
B 21/5
C 5
D 1/5
ja obliczyłem do momentu cosα=√21/5
17 sty 21:58
prosiaczek: A takie coś zrobicie: an=log(n2+1)
Oblicz an>100
log(n2+1)>100 i nie wiem co dalej
17 sty 21:59
DZIADZIA: to jak Basiek?
17 sty 22:04
Basiek: | | 2 | | π | |
sinα= |
| => cosα=√1−sin2α i dla α∊(0, |
| ) cosα>0 |
| | 5 | | 2 | |
| | 21 | | √21 | |
cosα=√ |
| => uwzględniając założenie cos>0 −> cosα= |
| |
| | 25 | | 5 | |
| √21 | | 5 | |
| ={√21} * |
| = 5 |
| cosα | | √21 | |
skróciło się, przy dzieleniu przez ułamek−> zamieniasz na mnożenie i odwracasz drugi składnik
17 sty 22:06
Godzio: prosiaczek ciekawe zadanie, rozwiązanie nie jest super banalne, ale do rozwiązania,
najpierw zapytam,
kylo,
Basiek mam nadzieję, że próbujecie
17 sty 22:06
prosiaczek: dziękuję
17 sty 22:09
ZKS:
Godzio jak kolokwium?
17 sty 22:09
Mila: JUż obliczyłam. Podać wynik?
17 sty 22:10
jarke: może i ja wrzucę zadanka:
Na ile sposobów można rozmieścić 9 chłopaków w trzech 3−osobowych pokojach.
i
Na ile sposobów można podzielić 10 osób na dwie 5−osobowe grupy.
prosiłbym o zdanie komentarzu, albo tok myślenia.
17 sty 22:10
Godzio:
Ja dam takie rozwiązanie
n
2 + 1 > 10
100
n
2 > 10
100 − 1
n >
√10100 − 1
Więc nierówność zachodzi na 100% dla n = [
√10100 − 1 ] + 1 gdzie [ x ] to część całkowita
z x
17 sty 22:11
Basiek: Ej, stop. STOP.
Miejsce do podawania zadań jest na forum, nie tu.
OUT. Dla porządku.
17 sty 22:12
Godzio:
ZKS rzeźnicze, ale udało mi się zrobić 4/5 zadań, z tego co słyszałem to mało komu udało
się zrobić dobrze więcej niż 2 zadania, także jest nieźle
17 sty 22:12
Basiek: Doszłam do postaci n>
√10100−1
Ale tego "więc nierówność..." nie wydusiłbyś ze mnie nawet na torturach. Dalej byś nie wydusił.
17 sty 22:14
prosiaczek: a ja mam w odp. takie coś
a
1050,a
1050+1....
17 sty 22:15
ZKS:
Ee to w porządku jeżeli 4/5.
Ciekawe jakie nam dowali kolokwium ale mam nadzieje że się to
ogarnie.
17 sty 22:16
Godzio:
Wszyscy mieli, że chociaż całkę da w miarę dobrą, to co ?
oblicz ∫f(x) jeśli
| | ⎧ | x√x − 1 | |
| f(x) = | ⎨ | √x − x2 |
|
| | ⎩ | 0 | |
Z obliczeniem większych problemów nie było, ale dobrać stałe już trochę gorzej
Ale dało
radę
17 sty 22:18
Godzio:
prosiaczek co to jest a1050 ?
17 sty 22:21
ZKS:
Ciekawe zadanie no my to troszkę chyba łatwiejsze będziemy mieli hehe.
17 sty 22:22
Godzio:
Ale dowodziki królowały
17 sty 22:23
prosiaczek: a − w podstawie logarytmu jest 1050, dziwnie napisałem
17 sty 22:24
prosiaczek: znaczy w podstawie 1050
17 sty 22:24
Godzio:
To jest wyraz a
1050
17 sty 22:26
ZKS:
Te dowodu u Ciebie to jakaś rzeź jest.
17 sty 22:27
Godzio:
No to można i tak, bo
√10100 − 1 <
√10100 = 10
50 = n
Czyli dla a
1050 jest już dobrze
17 sty 22:28
Godzio:
Najłatwiejszy:
| | 1 | | 3 | |
Uzasadnij, że |
| = cosx ma dokładnie jeden pierwiastek w przedziale ( |
| π,2π) |
| | x | | 2 | |
Ogólnie jedno zadanie około A4 zajmowały
17 sty 22:31
ZKS:
I mówisz że to najłatwiejsze?
To nie chciałbym wiedzieć tych najtrudniejszych.
17 sty 22:39
prosiaczek: a gdzie znikło −1?
17 sty 22:41
Godzio:
| | 1 | |
Def. funkcję: f(x) = cosx − |
| |
| | x | |
Trzeba pokazać, że istnieje takie a należące do tego przedziału, że f(a) >/< 0
i b takie że f(b) </> 0 (odpowiednio) więc po drodze przetnie OX, no to zachodzi dla głupich a
i b
i do tego pochodna musi być dodatnia i ujemna na tym przedziale, (ta druga część
rozwiązania już prosta
)
17 sty 22:43
Godzio:
prosiaczek nierównością pojechałem
17 sty 22:43
prosiaczek: no tak, ale jakoś nie wiem skąd to się wzięło
17 sty 22:47
ZKS:
To widzę że egzamin nie będzie Ci ani trochę straszny.
17 sty 22:48
Godzio:
Ta, wykuje milion twierdzeń i będzie dobrze
17 sty 22:52
ZKS:
Dobra ja jeszcze idę pouczyć się na krechę. Dobranoc.
17 sty 23:00
Godzio:
Dobranoc
17 sty 23:01
Basiek: bry
Mógłby mi ktoś sprawdzić dowód, gdybym zapisała? Nie jest trudny, ale nie wiem, czy tak
wystarczy, czy może coś zgubiłam, bo za ładnie to nie wyszło
18 sty 21:44
Mila:
Pisz!
18 sty 21:54
Mila: Zobacz ciekawe zadanie u Stanisława.
18 sty 21:57
kylo1303: Basiek Jak bedziesz chciala to moge dac w miare ciekawe zadanie z planimetrii (moze nie
tak ciekawe jak zadania od Godzio czy ZKS ale tez jest co robic.
18 sty 22:09
Godzio: Cholera, nie zaliczę logiki ...
Egzamin mnie czeka
18 sty 22:11
Basiek: Ej, robię sobie ten arkusz, który ostatnio na forum królował
Znaczy próbuję ! Ale tu gg, skype, fb... Normalnie, załamię się. Zadanie wrzuć, postaram się go
zrobić np. do poniedziałku, co?
18 sty 22:13
Basiek: Uzasadnij, że 6116<1824
61
16−18
24<0
(61
8)
2−(18
12)
2<0
(61
8−18
12)(61
8+18
12)<0
(61
8+18
12)>0 wynika z .... wiadomo.
stąd :
(61
8−18
12)(61
8+18
12)<0 ⇔ (61
8−18
12)<0=>
(61
4)
2−(18
6)
2= (61
4−18
6)(61
4+18
6)= (61
4+18
6)(61
4−18
6)=
(61
4+18
6)(61
2+18
3)(61
2−18
3)
Badamy znak: pierwszy składnik>0
drugi>0
trzeci... rozłożyć nie umiem..., więc (61
2−18
3)= 3721−5832<0
⇒wyrażenie (61
8−18
12)<0 ⇒ 61
16−18
24<0
c.n.u.
Sprawdzi ktoś? Proszę
18 sty 23:03
Eta:
61
16 < 64
16 =(4
3)
16=16
24 < 18
24
c.n.u
18 sty 23:09
Godzio:
61
16 < 64
16 = (16
3/2)
16 = 16{24{ < 18
24
O to chodziło
Ecie
18 sty 23:11
Eta:
(4
3)
16= 4
48= (4
2)
24= 16
24
18 sty 23:15
Basiek: Ekhem... nie bardzo rozumiem, ale rozszyfruję.
Twoje rozwiązanie
Eta jest... cóż, piękne, ale moje bardziej... spektakularne. Niemniej
jednak, dziękuję
18 sty 23:15
Godzio: Chyba że tak
18 sty 23:15
18 sty 23:17
ZKS:
Godzio czemu mówisz że nie zaliczysz logiki?
18 sty 23:17
Basiek: Okej, z wskazówką
Godzia rozumiem, ale
Ety już nie.
Cóż, taki mój żywot, a te moje wypociny będą ok?
18 sty 23:20
Godzio:
Bo popatrzyłem tylko na koło i ... jakby to powiedzieć, uczyłem się lecz WSZYSTKIE zadania
prócz jednego mnie zaskoczyły trudnością ... coś tam z neta spisałem, ale na pewno nie starczy
na zaliczenie ...
18 sty 23:21
Godzio:
To nie wskazówką Godzia, tylko inny zapis rozwiązania [P[Ety]
18 sty 23:21
Godzio: Ety *
18 sty 23:21
Eta:
zad1/ porównaj liczby: 9100 i 32600
zad2/ 12723 i 51318
18 sty 23:22
Basiek: Ogarniam.
Dziękuję dobrzy ludzie
18 sty 23:22
Godzio:
Eta dla
Baśki to zbyt banalne te zadania
18 sty 23:27
ZKS:
Oj tam oj tam zaliczysz.
Ja jutro mam wyniki z kolokwium z krechy ciekawe ile razy będę to
poprawiał.
18 sty 23:27
Godzio:
Logiki teraz nie zaliczę na pewno
Ale życzę, żebyś Ty zaliczył
Co do mnie, najważniejsza algebra i analiza, a z tym problemów nie mam, logikę zawsze mogę
poprawić bo niczego mi nie blokuje
18 sty 23:28
Basiek: 1)
3
200 < (32
3)
200
2)
(127{23/18)
18 513
18
18 sty 23:31
ZKS:
Jeżeli ja jutro zaliczę krechę to Ty tym bardziej logikę.
Może facet już Ci odpuści to jak
zauważył że jesteś jednym z najlepszych na kierunku to też będzie na to inaczej patrzył.
Patrzyłem w empiku ile kosztuje Battlefield 85zł więc całkiem nieźle.
18 sty 23:32
Godzio:
Ale on raczej nie wie, że jestem dobry z czegoś innego
Bo nawet nie ma dostępu specjalnie do
moich wyników z innych przedmiotów,
W takim razie już niedługo sesja się skończy i próbujemy coś grać
18 sty 23:34
Eta:
zad3/ Dany jest trójkąt ABC o bokach a,b,c >0 i kątach α,β,γ
| | b2+c2−a2 | | tgβ | |
wykaż,że |
| = |
| |
| | a2+c2−b2 | | tgα | |
zad4/ Podaj liczbę podzielników liczby
2000
zad5/ Wykaż,że jeżeli log
2b+log
2c +1 = log
2(b
2+c
2) , a,b,c>0
to b=c
P.S. Zadania przeznaczone dla
Basiek !
18 sty 23:35
Godzio: @Basiek
127 to coś w stylu 128, a
513 to coś w stylu 512
z czymś Ci się to kojarzy (to jest moje skojarzenie, jak zrobić to zadanie)
18 sty 23:35
Godzio:
Eta nie sądzisz, że 4 jest nieco pracochłonne jeśli się nie zna wzorku
? (a co tam
niech się męczy
)
18 sty 23:36
Basiek: Tortury specjalnie dla mnie? Kocham Was, naprawdę
18 sty 23:36
Basiek: zad 4) 20?
18 sty 23:39
Eta:
Godzio .........
( zad. dla
Basiek !
18 sty 23:39
Godzio:
Znasz wzorek
Oszukujesz
(tak 20
)
18 sty 23:40
Eta:
Widzisz
Godzio ? (zad4) ......... jak Basiulek trzaska zadanka
18 sty 23:41
Basiek: Eee, wzoru nie znałam
wiedziałam jak obliczyć, ponieważ robiłam takie zadania wczoraj lub
przedwczoraj
Jestem miszczem.
18 sty 23:42
Eta:
No to liczba podzielników liczby 2 520
18 sty 23:44
Godzio:
18 sty 23:44
Basiek: 48 ?
18 sty 23:48
Godzio:
Cholipka umie to
18 sty 23:51
Eta:
ok ...........
18 sty 23:51
Basiek: b5) L= log2(2bc)
porównujemy , bo te same podstawy
2bc= b2+c2
b2−2bc+c2=0
(b−c)2=0 ⇔ b=c cnu.
18 sty 23:51
ZKS:
To ja dam jeszcze zadanie i pójdę jeszcze się pouczyć.
Rozwiąż nierówność:
log
1253log
x5 + log
98log
4x > 1.
18 sty 23:53
Basiek: To ja zrobię !
Ale ostatnie na dziś, ok? ;>
18 sty 23:56
Godzio:
No jeszcze 3 zadania Ci zostały
18 sty 23:57
Basiek: Nie, kategorycznie odmawiam
18 sty 23:58
Eta:
Nie będzie tak lekko
za parę dni podam trudniejsze!
19 sty 00:00
Basiek: doszłam do postaci
teraz jeszcze jakoś pozmieniać postawy... postawię potem t, pytanie tylko, czy do tego momentu
jest ok
19 sty 00:03
Basiek: Doszłam do postaci
Tu moje morale osłabły i zdezerterowałam.
Dobranoc?
19 sty 00:09
ZKS:
| | 1 | | 1 | | 1 | |
Z |
| logx3 się zgodzę ale |
| log3x nie ta |
| mi nie pasuje. |
| | 3 | | 2 | | 2 | |
19 sty 00:13
Basiek: | 3 | |
| tam ma być |
| 4 | |
19 sty 00:17
kylo1303: Przepraszam ze tak pozno ale bylem zajety, zadanko mozliwe ze robilas, ale co tam:
W trapezie ABCD przedłużenia nierównoległych boków AD i BC są prostopadłe. Oblicz pole trapezu,
jeśli |AD|=a oraz |∡ABC|=|∡DAC|=α
19 sty 00:22
ZKS:
działaj.
19 sty 00:22
Basiek: Kylo dzięki, nic się nie stało. Jak widać na załączonym wyżej obrazku, nie nudzi mi się.
WIęc hm, doszłam do postaci t=log
3x
| 12+3t2−4t | |
| >0 (tu sobie 1nkę przeniosłam...) |
| 4t | |
⇔ 3t
2 −4t +12>0
Δ<0 − leżę i kwiczę.
19 sty 00:27
kylo1303: No widzialem ze Cię tutaj katują. Ja to juz znikam zeby i mi sie nie dostalo
Jutro zajrze to
porobie te zadanka. Powodzenia i dobranoc.
19 sty 00:29
ZKS:
| 1 | | 3 | |
| logx3 + |
| log3x > 1 / * 12 |
| 3 | | 4 | |
| 4 | |
| + 9log3x > 12 / * log3x |
| log3x | |
9log
23x − 12log
3x + 4 > 0
19 sty 00:30
ZKS:
Tak powinienem zrobić bo nie wiadomo czy x ∊ (0 ; 1) czy x ∊ (1 ;
∞)
| 9log23x − 12log3x + 4 | |
| > 0 / log23x |
| log3x | |
log
3x(3log − 2)
2 > 0
19 sty 00:33
Basiek: Mhm, dziękuję, rozumiem. Po prostu w pewnym momencie się zapętliłam i zamiast wrócić do
nierówności, co by wiele pomogło błądziłam gdzieś w logarytmach (których NIE lubię !).
Teraz jasne, dokończę
19 sty 00:33
ZKS:
Dobra ja już idę na spanie.
Dobranoc.
19 sty 00:34
Basiek: x>1
19 sty 00:35
Basiek: Dobranoc, dzięki
19 sty 00:36
ZKS:
I jeszcze wyrzucić trzeba z tego 3
2/3.
Branoc.
19 sty 00:45
Joanna: Witam.mam ogromną prośbę o rozwiązanie zadan ze statystyki.prosze o odpowiedz na e−maila
lesiek1@buziaczek.pl byłabym wdzieczna.pilne!
Zadanie 1
Podac przykład pary cech jakościowych w których pierwsza przyjmuje trzy wartości, a druga dwie
wartości. Na podstawie kilku objętości elementowe próby (przyjąć n) zbudować przykładową
tablicę dwudzielczą chcąc obliczyć na czego miarą jest x do kwadratu (hi kwadrat)
zadanie 2
Podac przykład zbiorowości oraz określonych na tej zbiorowości dwóch cech ilościowych ciągłych
miedzy ktorymi moze zachodzić związek przyczynowo−skutkowy, na podstaWIE 4 par przykładowych
wartosci rozwazanych cech obliczyc wspolczynnik korelacji i podac jego interpretację.
zadanie 3
Wsród 5 wyrobów są dwa wadliwe.określić rozkład prawdopodobienstwa przyjmującej wartości równe
liczbie wyrobu dobrych wśród dwoch wylosowanych. Obliczyć wartość oczekiwaną tej zmiennej
losowej
zadanie 4.
Czas pracy pewnego urządzenia jest zmienną losową o rozkładzie X:N (n 6) . Przyjąc samemu,
np(6) jaką część z dużej partii urządzeń będzie działać krócej niż m−6
zadanie5.
Wyznaczyć realizację 90% przedziału ufności dla wartości oczekiwanej m(do potęgi n) pewnej
cechy X (zdefiniować tą cechę) na podstawie próby losowej o licznosci n (większe lub równe)
nieskończoności (przyjąć n) zinterpretować uzyskany wynik, przyjąć X(z kreseczką na górze) ,
s.
19 sty 03:07
kylo1303:
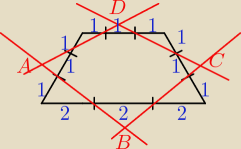
Takie zadanko dla wszystkich (nie mam odpowiedzi jbc):
Mamy trapez rownoramienny, ramiona sa dlugosci 3 jednostek, tak samo jak krotsza podstawa.
Dluzsza podstawa ma 6 jednostek. Kazda krawedz zostalo podzielona na 3 rowne czesci. Nastepnie
poprowadzono proste przechodzace przez pkt. na sasiadyjacych bokach (tak jak narysunku).
Oblicz pole powstalego czworokata ABCD.
19 sty 21:46
Basiek : Może jakieś zadanie na tę okazję?
Ech...
3 lut 23:31
Godzio: Jaką okazję
?
3 lut 23:32
Basiek : A nie wiem, podobno Polak zawsze znajdzie okazję
3 lut 23:33
Godzio:
To taki banalik na początek:
log320 = a
log315 = b
Wyznacz log2(360) (w zależności od a i b)
3 lut 23:35
ZKS:
Jaki dział?
3 lut 23:35
Basiek : Wyciągnę materiały piśmiennicze itd.
Dzięki
Godzio, a w ogóle to witaj. Tak od końca trochę, ale trudno
3 lut 23:36
Godzio:
No witam
ZKS w niedziele gramy haha
?
3 lut 23:37
ZKS:
Miejmy nadzieje
Godzio.
3 lut 23:38
Basiek : Cześć
ZKS, obojętnie. Czas włączyć myślenie. 3 dni całkowitego nic nie robienia źle na
mnie wpływa.
3 lut 23:38
ZKS:
Witaj
Basiek!
Nie ma obojętnego działu powiedz jaki i coś się poszuka.
3 lut 23:40
Basiek : Boże... nie wiem. Geometria na płaszczyźnie?
3 lut 23:41
ZKS:
Dane są dwie rodziny figur A
m i B
m gdzie
A
m = {(x ; y): |x| + |y| ≤ m ∧ m ∊ R
+}
B
m = {(x ; y):4x
2 + 4y
2 − 4x ≤ 4m − 1 ∧ m ∊ R
+}
Dla jakich wartości parametru m prawdziwa jest inkluzja B
m ⊂ A
m?
3 lut 23:47
Basiek : Jej, jak ja nienawidzę logarytmów
Właśnie sobie to ponownie uświadomiłam.
Inkluzja to jest całkowite zawarcie? Czy co?
Pierwszy raz widzę ten wyraz, ale chyba mi się
podoba.
3 lut 23:50
ZKS:
Zawieranie się w czymś.
3 lut 23:51
Basiek : Świetnie ! A już się bałam, że się wyśpię.
3 lut 23:53
Godzio:
Tak chwilkę pomyślałem, nie takie straszne to zadanko
3 lut 23:56
ZKS:
Nie licz na to.
3 lut 23:56
ZKS:
Właśnie ono wydaje się straszne ale chwilkę się trzeba zastanowić i idzie.
3 lut 23:57
Basiek : Ej, ja tu serio mówiłam, że mój mózg od 3 dni nie pracował.
Ale za to jak się wyspałam...
3 lut 23:58
Godzio:
Baśkowi chyba trudno to będzie rozwikłać, myślę że dobrym pomysłem byłyby "pytania
pomocnicze" tzn.
Basiek, jak myślisz, co przedstawiają te rodziny ?
3 lut 23:59
Basiek : "rodziny" ?
4 lut 00:01
ZKS:
Właśnie
Basiek pisz jeżeli coś nie rozumiesz.
4 lut 00:01
Godzio:
np.
y = x
2 + m to rodzina parabol o wierzchołku (0,m)
4 lut 00:02
4 lut 00:04
ZKS:
Słuchaj uważnie i notuj co mówi Pan Profesor.
4 lut 00:04
Basiek : Baśkowe oczy widzą koła.
np. w tym drugim
4 lut 00:05
Godzio: Ale Ty chcesz na wsi studiować czy w mieście, bo nie wiem
?
4 lut 00:05
Basiek : Kogo pytasz i o co chodzi?
4 lut 00:06
Godzio: a to pierwsze to co ?
Ciebie
, to było a propo "NIE zrobię"
4 lut 00:07
Eta:
U mnie na wsi ?
4 lut 00:07
Basiek : Godzio, na wsi uniwersytetów jeszcze nie widziałam ;> .
Btw. w październiku witam się z Krakowem, jak przestanę się lenić i zdam maturę
4 lut 00:08
ZKS:
Jedna z idealnych figur zaczyna się na K... .
4 lut 00:08
Eta:
Krzywa K
4 lut 00:10
Basiek : Czekajcie, mogę korzystać z googli?
4 lut 00:10
Basiek : Krzywa Kocha
? Wczoraj o niej czytałam sobie w ramach czasu wolnego
4 lut 00:11
Eta:
A kogo ta krzywa kocha?
4 lut 00:12
Basiek : Fraktale. hahaha
4 lut 00:13
Basiek : Dobra, nie wiem, co przestawia
IxI+IyI≤m chyba, że ech... IyI=m−IxI , ale to wygląda tak bzdurnie... A google milczą!
4 lut 00:15
Godzio:
No to do roboty
|x| + |y| ≤ 1
Rozpatruj wszystkie przypadki i rysuj, co Ci wyjdzie ?
4 lut 00:16
Godzio:
Eta
4 lut 00:16
ZKS:
Jaka figura ma wszystkie boki i kąty równe?
4 lut 00:18
Eta:
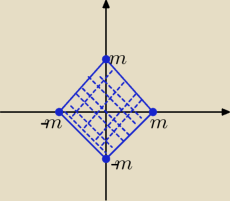
4 lut 00:18
Basiek : ^^
Kwadrat
4 lut 00:19
Eta:
Godzio ........ sorry, jak rysowałam to nie widziałam Twojego wpisu
4 lut 00:19
Basiek : Ale skąd takie coś się wzięło... to już nie wiem. Ale i tak fajne.
4 lut 00:20
ZKS:
Czyli to będzie wnętrze kwadratu wraz z krawędziami.
4 lut 00:20
Godzio: Trudno
Basiek zrób to co Ci zadałem, a będziesz wiedziała skąd to się wzięło
4 lut 00:21
Basiek : No łatwo powiedzieć...
że co mam pod co podstawiać?
4 lut 00:23
ZKS:
Zgodnie z tym co mówi
Godzio powinnaś otrzymasz 4 przypadki i zobaczysz skąd to co
narysowała
Eta się wzięło.
4 lut 00:25
Eta:
Przedziałami:
1/ x≥0 i y≥0 x+y ≤1 ⇒y ≤ −x +1
2/ x <0 i y ≥0 .........
itd ........
teraz maluj częściami .........
4 lut 00:26
Basiek : Aaaa, o te przypadki Ci chodziło.
Okej. Wyciągnę dla Ciebie nawet kartkę w kratkę !
4 lut 00:27
Eta:
Możesz też na czystej kartce namalować kratki
4 lut 00:28
Basiek : Ostatnio tak robiłam, ale hm... znudziło mi się po 5 kreskach
(i było strasznie koślawe...)
4 lut 00:30
Godzio:
Ja nie miałem kratki ostatnio i musiałem sobie drukować
4 lut 00:32
Eta:
4 lut 00:32
Eta:
4 lut 00:32
Basiek : Ech... mam !
i rozumiem nawet ;>
4 lut 00:33
Eta:
I o to szło
4 lut 00:33
Godzio:
Ja na razie uciekam sobie pograć, wpadnę niedługo zobaczyć postępy (liczę, że jak uporasz się z
zadaniem od
ZKS to moje też pykniesz
)
4 lut 00:34
Eta:
To ja też zagram ...................w brydża
4 lut 00:35
4 lut 00:35
Basiek : | | 2−√3 | | 2+√3 | | 2+√3 | |
m∊(−∞, |
| >u< |
| ,+∞) ⋀ m∊R+ ⇔ m∊(0,{2−√3}{2}>u< |
| ,+∞) |
| | 2 | | 2 | | 2 | |
Teraz można krzyczeć.
4 lut 00:44
ZKS:
I jak idzie zadanko?
4 lut 00:44
ZKS:
Prawie dobrze bo odpowiedź jest :
4 lut 00:45
Eta:
Pojawił się
pigor .......... zaraz Ci wyjaśni łopatologicznie
Dobranoc Wszystkim ...
4 lut 00:46
Basiek : A teraz pytanie, gdzie jest w takim wypadku błąd? : O
4 lut 00:47
Basiek : Łopatologia w wykonaniu
Pigora i już wiesz, że nic nie wiesz.
Dobranoc
Eta
4 lut 00:48
ZKS:
A czy rozważałaś jeden czy dwa warunki?
4 lut 00:50
ZKS:
Dobranoc
Eta .
4 lut 00:50
4 lut 00:51
Basiek : Tylko jeden.... jaki będzie drugi?
4 lut 00:51
ZKS:
To jest jeden tylko warunek a drugi?
4 lut 00:52
ZKS:
Środek koła będzie należał do A
m.
4 lut 00:53
Basiek : Zabiłbyś mnie, ale uwierz... na to bym nie wpadła.
4 lut 00:54
ZKS:
Nie śmiałbym Cię tknąć a co dopiero zabić.
4 lut 00:57
ZKS:
I jak wyszło wszystko?
4 lut 00:58
Basiek : Czymże sobie na nietykalność osobistą zasłużyłam?
Ech... znam warunek, ale nie bardzo umiem zapisać?
4 lut 00:59
ZKS:
| | 1 | | 1 | |
| |
| | + |0| ≤ m ⇔ m ≥ |
| i teraz koniunkcją warunku 1o i 2o i powinnaś otrzymać |
| | 2 | | 2 | |
wynik.
Hmm swoją osobą (jesteś kobietą).
4 lut 01:02
Basiek : Dobra.
| | 1 | |
| |
| | + |0| ≤ m na to bym raczej nie wpadła, bo nie do końca pojmuję zastosowanie zapisu: |
| | 2 | |
|x|+|y|≤ z , choć sam zapis już rozumiem...
+ mam jeszcze jeden "problem" , w odp. jest otwarty przedział, a chyba powinien być
lewostronnie domknięty. (?)
Hm, lubię te staroświeckie zasady, typu "Kobiet się nie bije"
4 lut 01:06
ZKS:
Bo jest samo ⊂ .
4 lut 01:12
Basiek : Wlazłam na taką stronę ... , czy to czasem nie jest zadanie z działu "topologia− przestrzeń
Euklidesowa"?
....
4 lut 01:14
Basiek : Albo i nie...
Zresztą, to mało istotne. Uwaga− nie czepiam się
4 lut 01:17
ZKS:
Nie wiem może ale wiem że mam to zadanie pod Geometrią Analityczną.
4 lut 01:19
ZKS:
To teraz zadanie zrób zadanie które podał
Godzio.
4 lut 01:23
Basiek : Co do
Godziowego− wstyd się przyznać, ale chyba też gdzieś się zapętliłam.
| | log3 360 | | log3(9*40) | |
log2 360= |
| = |
| = U{3+ log3 40}{log3 30− |
| | log3 2 | | log3(30:15) | |
a}=....
i obawiam się, że wzory, które pozwolą mi przekształcić log
3 40 na coś z 2−jką i log
3 20 Nie
istnieją, tak samo jak log
3 30
4 lut 01:24
Basiek : Po ułamku− poprawkę robię, mimo że jest źle:
4 lut 01:26
Basiek : | 2+log3(20*2) | | 2+log3 2+ a | |
| = |
| = |
| log3(15*2)−a | | b−log32−a | |
I tak wtopiłam
4 lut 01:29
Basiek : log
3 2
Uff.
4 lut 01:30
ZKS:
A te magiczne log
32?
4 lut 01:32
Basiek : log
32= log
3(3*20 : 2*15)
Ale niestety tego chyba nie rozpiszę
4 lut 01:35
ZKS:
Wykombinowała coś Pani?
4 lut 01:35
Basiek : Nie. I chyba już nie wykombinuję. Nie wiem, co za głupek wymyślił, że kobiety są najlepsze w
wymyślaniu, kombinowaniu i krętaczeniu
4 lut 01:37
ZKS:
Nie kombinuj się wykręcać z tego zadania.
Wykupujesz wskazówkę?
4 lut 01:41
Basiek : Ech. Do mnie się mówi jednoznacznie, żebym nie miała skojarzeń. Weźcie wszyscy zapamiętajcie.
Wskazówka?− biorę.
Słowo "wykupować" jednoznacznie kojarzy mi się z zapłatą. Tu pytanie nasuwa się− jaką?
4 lut 01:43
ZKS:
A jaką chcesz.
Wiemy że
| | log35 − a | |
a = log320 = log35 + 2log32 ⇒ log32 = |
| |
| | 2 | |
Podobnie zamień b.
4 lut 01:46
Basiek : | | a−log3 5 | |
log32= |
| chyba |
| | 2 | |
b=log
3 15= log
3 (3*5)= 1+log
35= > log
35=b−1
4 lut 01:50
ZKS:
Oczywiście późna pora dlatego zaraz idę na spanie.
4 lut 01:52
Basiek : To wcale nie było czepianie się.
Wiesz, ile razy to sprawdziłam, zanim śmiałam stwierdzić,
że być może przez przypadek się pomyliłeś z głupim znakiem?! No.
| | 3a−b+5 | |
Wyszło mi ostatecznie: |
| |
| | −3a+3b−1 | |
4 lut 01:55
Godzio:
Sprawdzam
4 lut 01:56
Godzio:
| | 3a − b + 5 | |
Źle, |
| powinno być |
| | a − b + 1 | |
4 lut 01:57
Basiek : Spójrzmy więc na sam mianownik:
| | a−b+1 | | 2b−a+b−1−2a | | −3a+3b−1 | |
b−log3−a= b− |
| −a= |
| = |
| , dwójeczki się skrócą z |
| | 2 | | 2 | | 2 | |
licznikiem.... −3a+3b−1 w mianowniku mi wychodzi.
Co znów zrobiłam?
4 lut 02:00
Godzio:
Poszukam błędu, (nienawidzę tego, ale znajdę
)
4 lut 02:04
Godzio:
Na początku: log
3(9 * 40) = 2 + log
340 a nie 3 + log
340
4 lut 02:05
Basiek : Poprawiłam przecież już później to
4 lut 02:05
Godzio: Dobra widzę korektę
4 lut 02:06
Basiek : No, widzisz. Ale i tak idę o zakład, że błąd będzie baaardzo głupi.
4 lut 02:07
Godzio: Mianownik mi się nie podoba na samym początku coś
4 lut 02:09
ZKS:
Chyba znalazłem.
4 lut 02:10
Basiek : Co znów takiego
be zrobiłam?
4 lut 02:11
Godzio:
| | ... | |
Powinno być |
| |
| | log330 − b | |
4 lut 02:11
ZKS:
Właśnie.
Nie a tylko
b.
4 lut 02:12
Basiek : Hm, dobra, dobra... zrobię sobie jeszcze raz!
Ale dzięki chłopcy, jesteście wieeelcy. <wiadro jabłek>
4 lut 02:14
Basiek : Teraz mi wyszło (aż się pochwalę!) w mianowniku
−a
+b+1
4 lut 02:23
ZKS:
albo skoro masz alergie na jabłka to
.
4 lut 02:25
Basiek : Już nie mam
Ale i tak wolę kwiatki
Dziękuję.
<Kiedyś mi wyjdzie, wiem to!>
4 lut 02:27
Basiek : Wyszło! Za jakimś 4−tym razem, ale oto jest wynik!
4 lut 02:30
ZKS:
A proszę Cie bardzo.
No to ja już lecę na spanko.
Dobranoc
Godzio i
Basiek.
4 lut 02:31
Basiek : Dobranoc
Jeszcze raz dzięki
4 lut 02:32
Godzio: Dobranoc
4 lut 02:33
4 lut 02:35
Eta:
Kiedyś to była
nauka ! aż miło poczytać
3 lis 19:11
Mila:
3 lis 19:14
Eta:
Mila mam rację ?
na zdrowie
3 lis 19:20
Mila:
Młodzież ma korona ferie
3 lis 20:10
