pierwiastek: czy dzięki zdefiniowaniu funkcji trygonometrycznych dowolnego kąta mogę obliczyć boki w każdym trójkącie (nie tylko prostokątnym)?

Jakub: W trójkątach, innych niż prostokątne, najlepiej stosować twierdzenie sinusów (549) i cosinusów (543).

magda: a skąd mam wiedziec który kąt obliczam?

Jakub: Zbyt ogólne pytanie. Zależy od sytuacji. Podaj konkretny przykład.

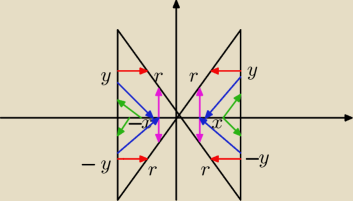
Gustlik: Schemat "strzałkowy" obliczania funkcji trygonometrycznych dowolnego kata Legenda: sinα cosα tgα ctgα UWAGA ! x, y, −x, −y oznaczają WSPÓŁRZĘDNE, NIE DŁUGOŚCI PRZYPROSTOKĄTNYCH, dlatego mogą być one ujemne ! Promień wodzący r jest ZAWSZE DODATNI !

a ja mam pytanie: a co to jest sinus lgn? bo mam takie zadanie, żeby uzasadnić, że wykres tej funkcji można wpisać w czworościan!

Anonymous: W takim razie jak obliczyć wartości sin/cos/tg/ctg dla trójkątów z kątem większym od 90 stopni? Trójkąt rozwarty nie ma już przecież kąta prostego, bo suma stopni musi wynosić 180. Jak wtedy mamy wiedzieć gdzie jest przeciwprostokątna i przyprostokątne skoro ich nie ma? I jak ma wyglądać ten przedłużony trójkąt (o zwiększonym kącie, by wychodził poza I ćwiartkę)?

zdzisłowyzdzisia: Pożyteczna strona polecam zdzisłowyzdzisia . ⬡

kaś: Mam problem z rysunkiem na stronie. Skoro te wzory służą do obliczania kątów większych niż 90 stopni, to dlaczego jest zaznaczony kąt ostry a nie rozwarty tak jak w przykładowych zadaniach?

Jakub: Z tych wzorów można też wyliczyć wartości funkcji trygonometrycznych dla kątów ostrych, Przy takim rysunku łatwiej zapamiętać te wzory, ponieważ wynikają one wprost z definicji funkcji trygonometrycznych dla kąta ostrego ze strony 397.

Stanisław: Jeżeli mamy podany punkt P (5,−5) i mamy wyznaczyć kąt między ramieniem kąta a układem, to np z tangensa nam wychodzi −1. Czy da się z samych wzorów wyliczyć ze ten punkt znajduje się w IV a nie II ćwiartce (tanges ten sam) czy w tych przypadkach na dostawie podanych współrzędnych definiuję że jest to 315 a nie 135?

Jakub: Jak rozumiem chodzi Ci o to, że dla tgα = −1 kąt α może być równy zarówno 135^o jak i 315^o. Dla obu tych kątów tangens wynosi −1. Rozwiązaniem jest policzenie sinα. Dla α = 135^o sinus jest dodatni a dla α = 315^o sinus jest ujemny. Tak więc liczysz jednocześnie tangens i sinus α i na tej podstawie wyznaczasz wartość i znak wartości kąta α.