Ola: sprawdz,czy liczba 2 jest dwukrotnym pierwiaskiem wielomianu W(x)=xdo4−xdo3−13xdo2+32x−20

Ola: Ola: sprawdz,czy liczba 2 jest dwukrotnym pierwiaskiem wielomianu W(x)=xdo4−xdo3−13xdo2+32x−20

Adrianek: super

emcio:

Mateusz:

2x − 5		10 − 4x
	:
3		−12

Jakub: Zadania umieszczajcie na forum zadankowym

Gos: wszystko super wyjasnione... rozumiem, potrafie zrobić... a na sprawdzianie wychodzi... nie powiem co bo to niezbyt przyjemne słowo... ja nie wiem... chyba jestem głupia i nie nadaje się do Liceum...

Jakub: Spokojnie to minie z czasem. Rób dużo zadań ze zbiorów i w pewnym momencie sama poczujesz, że jest lepiej.

Gos: dzięki za dobre słowa Jakub staram się jak mogę... ale często robię głupie błędy, bo nie rozumiem polecenia...

Gos: ale ta strona jest świetna... dzięki niej jestem w stanie to w ogóle pojąć, bo na matematyce niestety lekcja nie wygląda jak lekcja tylko jak wyścig z czasem, żeby nadążyć z materiałem...

luub: naprawde super strona

Ana 1991: co z tym zrobić?(x−2)(x+3)(2x−8)=0

Ana 1991: x=2 x=−3 x=4 i co dalej

Jakub: To są miejsca zerowe wielomianu (x−2)(x+3)(2x−8), czyli rozwiązania równania. Koniec zadania.

Schabowy: Fajna strona, tylko szkoda, że 1. mało zadań, 2. w większości temat nie został wyczerpany. Mam nadzieję, że się postaracie

Jakub: Ja też mam nadzieję Postaram się postarać.

maturka za 5 dni ;): świetna strona wszytsko wytłumaczone jak trzeba − bardzo mi pomogła nie pierwszy raz. Gartuluję!

tri: Dlaczego tutaj pisze że nierówność wielomianowa jest na poziomie rozszerzonym, robię teraz dużo zadań z poziomu podstawowego i jest jej bardzo wiele...?

Jakub: Zobacz standardy maturalne 2010 http://www.cke.edu.pl/images/stories/Inf_mat_08/mat_informator_10.pdf

scenecunt@wp.pl: autorze, jestes wspanialy. bardzo mi pomaga twoja strona! bardziej niz zwykle zajecia w liceum dziekuje!

wqable: za każdym razem gdy korzystam z Twojej strony, zastanawiam sie po co ja właściwie do tej szkoły chodzę... na lekcji nic nie rozumiem a trwa godzine, a tu wystarczy że spojrze, powtórze i wszystko staje sie jasne w 5minut. dziekuje. POZDRAWIAM.

Kapeluszowiec: Normalnie EXTRA stronka

Imię lub nick: Witam, mam pytanie : Skąd mam wiedzieć jak rozłożyć na czynniki coś takiego jak to wyrażenie niżej ? x³ + 3x² +15x − 17 = 0 Jest na to jakaś metoda ? Jakiś schemat postępowania ?

Barzu: Dziękuję 4+

wb: Wielkie dzięki Ziomal. Jesteś wielki. Dzięki Twojej stronce zdałem poprawkę. Jak będziesz w Wielkopolsce to się odezwij, masz u mnie zgrzewe piwa, Pozdro!

Jakub: Będę pamiętał

Gośka: hmm .. strona jest Superaśna dużo jest wiadomości i jest okey ale brakuje mi np. równań i nierówności z wartością bezwzględną .. z tym mam największy problem ... głównie się to tyczy wielomianów

Jakub: Na stronie 1807 i 2545 masz trochę.

Ewelina J.: Bardzo fajna strona ... Jednakże jako nauczycielka stwierdzam ze rzeczywiscie dział wielomianow jest sporo "okrojony"... Może udało by sie jakos to uaktualnić jakby co mogę pomóc

bajka_0909: Witam, Czy można zamieścić jakieś zadania ze studiów dot. macierzy?

wiolka23: czy mozesz mi napisac jakie bedzie rozwiazanie nierownosci x(x² +1)(1−x)(2x+3)²≤0 ? mi wyszlo x nalezy do<0;1> ,czy to jest dobrze?

wiolka23: i zgadzam sie z bajka 0909...prosze o macierze!czarna magia...zwlaszcza przepływy miedzygaleziowe!

Jakub: Macierze są w planach, tylko na razie czasu brak.

marika: hej mam pytanie nie wiem jak zrobić to zadanie może ktoś mi pomoże oto właśnie to zadanie: dane są wielomiany W(x)=2x²−5x+3 i P(x)=x³−5x²+2x−1.wyznacz wartość wielomianu G(x)=2W(x)−P(x) proszę o szybką odp

mac: A dział o rysowaniu wykresów lub co innego się pojawi? Bo chyba na maturze 2008 było z tego co pamiętam.

Jakub: W dziale "nierówność wielomianowa" masz przybliżone rysowanie wykresów. O którym zadaniu z matury 2008 piszesz?

kasiula: Wartość wielomianu W(x) = x3 + rx2 + sx + t dla x = 1 wynosi −2, czyli W(1) = −2. Wiadomo też, że W(−1) = −10 i W(0) = −4. Znajdź wartości współczynników r,s,t.

Bartek: Witam Proszę o pomoc w rozłożeniu na czynniki tego wielomianu W(x)= 36x² − (4 − 3x²)² Wydaje mi się że robię błąd przy potęgowaniu, tak czy inaczej proszę o pomoc w rozwiązaniu całego zadania.

Bartek: i jeszcze coś takiego x⁶ −729

dejwi: matrobot.com darmowa strona dla ktorej dzielenie wielomianow to pestka. Rozwiazania z dokladnym wyjasnieniem jak dojsc do koncowego wyniku. Polecam

kik: a co z wiedzą na temat reszty z wielomianu nic nie znalazłam na ten temat ?

xerox: z parametrem tez mozna by jakies zadania zamiescic... bo musialem to powtorzyc sobie do spr i nie znalazlem tego tutaj

humanistka : Nieeeeeeee no czemu nie mam takiego nauczyciela od matematyki!? Jest Pan genialny! SERDECZNIE DZIĘKUJE za przybliżenie mi w tak łatwy i przyjemny sposób tego przedmiotu!

Angela: Proszę o pomoc wie ktoś jak rozwiązać równianie: a) 8x³⁴ − 32³² = 0 b) x⁴ −20x³ + 19x² = 0 Prosze o szybką odp.

asia: super strona dziękuje...nie musze grzebac w zeszytach zeby przypomniec sobie pierwsza klase a mam spr powtorzeniowe ..i ta stronka jest idealna.

przemek: Super strona!

KarinKa: :0 extra;>

Majka: Twórco tej strony! Nawet nie wiesz jak wspaniały jest jej wpływ na moje życie Podziwiam czytelność, logiczne uporządkowanie, świetne przykłady, dobre zadania, linki do konkretnych działów przy różnych częściach zadania które mogą się wydać niezrozumiałe, no i to że reklamy są przez Ciebie tak umiejscowione, że absolutnie nie irytują jak to się często zdarza na większości stron mających w czymś niby pomóc. Życzę Ci wygranej w totka, lub chociaż rzetelnych korzyści finansowych z tej strony

Jakub: Dzięki, muszę zacząć grać, bo jak mi już życzą, to może coś wygram

Muzicjohn: Ale fajne toto do rysunkow ^^. Wspaniala strona, samemu mozna sie wszystkiego nauczyc, wielkie dzieki za wlozona prace .

Ola: dany wielomian W(x)=−9x+4 P(x)=x²+2x−1 POMOCY PROSZE:(

ddd: Dany jest wielomian W(x) = x³ − x² + 1 Oblicz W(√2 + 1 ) oraz W(√3−√2) . Jak to zrobić?

Aga: Dzięki za stronkę! Będę w tym roku zdawać maturę rozszeżoną i cieszę się że tu trafiłam Moja obecna nauczycielka jest taaaak beznadziejna że sama sobie muszę przerobić 2gą kl. Nieby mam 5 a nic nie umiem Również życzę wygranej w totka.

Gustlik: Moje "poprawki" − tak powinien wyglądać program nauczania z tego działu: podstawy rozszerzenia studia wielomian, definicja, stopień, współczynniki wielomianu pierwiastek wielomianu, miejsce zerowe wielomianu dodawanie, odejmowanie, mnożenie wielomianów rozkład wielomianu na czynniki, postać iloczynowa wielomianu równanie wielomianowe dzielenie wielomianów schemat Hornera twierdzenie Bezout twierdzenie o pierwiastkach wymiernych wielomianu krotność pierwiastka wielomianu, odczytywanie pierwiastka wielomianu z postaci iloczynowej nierówność wielomianowa

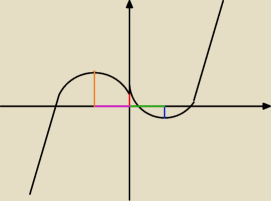
ebi: czy są jakieś wzory naposzczegółne z odcinków? wiem ,że dla f(x)=ax³+b²+cx+d czerwony odcinek ma długość d. a reszta?

Jakub: Jakiś ogólnych wzorów nie ma. W pomarańczowym odcinku funkcja ma maksimum, a w niebieskim minimum. Te ekstrema funkcji możesz wyznaczyć za pomocą pochodnej funkcji. Zobacz 387.

ebi: ok. dzieki!

ebi: ale jak

Jakub: Jak to ja ci nie napiszę, bo w podręcznikach to zajmuje cały rozdział. Zobacz przykład 389

ebi: wielkie dzięki

ebi:

	2b3+(−3b2+9ac)√b2−3ac−9abc+ (√b2−3ac)3+27a2d
f(x1)=
	27a2

	2b3+(3b2−9ac)√b2−3ac−9abc+(√b2−3ac)3+27a2d
f(x2)=
	27a2

η=(−3b²+9ac)√b²−3ac λ 2b³−9abc+(√b²−3ac)³+27a²d przy czym √b²−3ac>0 , czyli η>0 więc

	λ+η
f(x1)=
	27a2

	λ−η
f(x2)=
	27a2

harowalem trzy godziny ale sie oplacalo dzieki mistrzu co jest większe, to maksimum ,a co mniejsze − minimum. naprawdę wielkie dzięki

ebi: ups pod η=... ma byc λ=... moj blad

Gustlik: Jakubie, dla osób znających pochodne warto jeszcze dodać następujące twierdzenie: Jeżeli liczba a jest n−krotnym pierwiastkiem wielomianu W(x), to jest ona też pierwiastkiem pochodnych tego wielomianu do stopnia (n−1) włącznie. Krótko mówiąc: pierwiastek n−krotny jest pierwiastkiem danego wielomianu i (n−1) jego pochodnych, czyli w sumie jest pierwiastkiem n funkcji wielomianowych. Np. pierwiastek 2−krotny jest pierwiastkiem 2 wielomianów: W(x) i jego pochodnej W'(x) Pierwastek 3−krotny jest pierwiastkiem 3 wielomianów: W(x) i dwóch jego pochodnych W'(x) i W''(x) Pierwastek 4−krotny jest pierwiastkiem 4 wielomianów: W(x) i trzech jego pochodnych W'(x), W''(x) i W'''(x) itd... Przydaje sie to do rozwiązywania zadań typu: dla jakich wartości parametrów a i b liczba 2 jest 3−krotnym pierwiastkiem wielomianu W(x)=x⁴−5x³+ax²+bx−8? Zadanie pochodzi ze zbioru: Mirosława Gila − nauczyciela matematyki LO im. B. Chrobrego w Kłodzku. Zbiór można pobrać tutaj: http://www.chrobry.org/content/view/330 Polecam, zwłaszcza osobom zdającym matematykę rozszerzoną.

Jakub: Ciekawe twierdzenie i rzeczywiście dużo prościej jest nim posłużyć do rozwiązania zadania z wielomianem W(x)=x⁴−5x³+ax²+bx−8. Problemem jest jednak to, że nie ma pochodnych w programie liceum. Jednak podstawowe wzory na pochodne są na tyle proste, że chętni szybko je pojmą. Może faktycznie warto dodać stronę z takimi zadaniami dla chętnych.

PainM: 10000x²(5⁻³ y)² −−−−−−−−−−−−−−−−−−−−−−−−−−− = 25(x⁻¹:y)⁻³

koko: for you.

Jakub: ohh thanks

PerfectGirl: wreszcie wszystko w 1 miejscu dzięki wielkie......

Agata: nie wiem jak to rozwiazac to jest zadanie z ksiazki: 4x⁴ − 5x² + 1=0 Próbowałąm wszystkiego ale nie wychodzi mi wynik z ksiązki9musialam tu napisac bo nie umiem na tym forum zadankowym)

Jakub: Zobacz to zadanie 1388, a tu 1678 więcej przykładów.

Agata: dziekuje

Marcin: Szkoda, że te zadanie dla poziomu rozszerzonego są trochę za łatwe. Rozwiązałem wszystkie bez problemu, ale i tak na jutrzejszej pracy klasowej dostanę 2 w porywach 3. Brakuje mi tutaj tych naprawdę trudnych zadań. Ta strona jest idealna dla kogoś, kto się przygotowuje do matury podstawowej.

Daria: 1+6x+12x²+8x³≤0 (x−3)(x+6)(x−9)⁷ (x+5)³<0

karo: moje ukochane wielomiany ! <3

jurkiewka13: dziękuję za poświęcenie masy czasu na stworzenie tej stronki, dzięki niej wiele zrozumiałam

jedej09: x(x4(x+3)+2)=3(x+1) jak to rozwiązać ?

txh wielkie: jestes zajefajny gosciu jednak zgadzam sie z niektorymi osobami ze te zadanka sa dosyc proste jakbys mial chwilke czasu prosze zamiesc jakies trudniejsze

Szaman: Wielkie dzięki za zebranie wszystkiego w jednym miejscu − przyda się do matury

Mariusz: Witam, czy mogłbym komus na poczte przeslac moje zadania gdyz mam je zeskanowane? jesli tak bylbym bardzo wdzieczny

ewa: pomocy!plis pomóżcie mi będe wdzięczna! z(x)=(2x+3)(x(kwadrat)−x−2) z(x)=−x(kwadrat)(x(kwadrat)−9)(x(kwadrat)+1)

Kamila: proszę o pomoc w rozwiązaniu −2x¹⁴−5x⁸−4x⁶−1=0

Annnn: Wyznacz takie wartości a i b, aby liczby r1 i r2 były pierwiastkami wielomianu W(x) jeśli;

	1
c)W(x)=ax3 + x2 + bx − 1, r1= −		, r2= 1
	2

doszłam do tego układu równań i nie wiem jak mam dalej to obliczyć:(Mógłby ktoś pomóc?Proszę...

	1		1		3
−		a −		b −		=0
	8		2		4

a + b = 0

Jakub: Rozwiąż ten układ równań. a+b = 0 b = −a i podstaw za "b" do pierwszego równania.

Annnn: Nie wiem skąd się wziął ten układ równań który napisałeś.Bynajmniej mi nie wychodzi.

Hary:

dawid: Jakubie a co z wyrazeniami wymiernymi? nie widze tego nigdzie.

Jakub: Tutaj masz https://matematykaszkolna.pl/strona/i9.html

Coco: ale shit! nic z tego nie rozumiem te zadania, te dzialy, ktore ogarniam, tutaj sa wytlumaczone jakos kosmicznie o.O

zuza: A przypadkiem twierdzenie Bezout i dzielenie wielomianów nie jest na maturze podstawowej?

Jakub: Można sprawdzić https://matematykaszkolna.pl/strona/informator.html

dorotka: ≠

kamil: Oblicz wartość wielomianu dla x=0 a) x=2, x=1 w(x)=2x⁽3)−x⁽2)+x−4 b) w(x)=x⁽4)+2x⁽3)−6x+1

piotrek: Rozwiąż: a) w= −3x²+5x+2 b) w=3x²−4x⁴+4x³

dyzio: (1−2x)²−(1−2x)(x²+3)=0 (x−3)(2x+2)=(x−3)(x²−6) x²(2x−3)(x+2)=x³−2x²

ollaa: Pomocy ! Oblicz sumę wszystkich wsołczynników wielomianu w(x)jeśli a)w(x)=x⁶+2x⁵−3x⁴−5X³+2x+1 b)w(x)=2x⁵−3x⁴+6x³−x²+x+5

Justyna.: Oblicz w(−1) oraz w(−2) dla wielomianu w(x)=a₃x³ + a₂x² +a₁x+a₀ a) a₀=3 , a₁=4, a₂=0, a₃=−5 b) a₀=0, a₁=−2, a₂=−3, a₃=6

Justynaaa: będę bardzo wdzięczna ulżycie mi w 10 zadaniach Pomocy! Oblicz w(−1) oraz w(−2) dla wielomianu w(x)=a3x3 + a2x2 +a1x+a0 a) a0=3 , a1=4, a2=0, a3=−5 b) a0=0, a1=−2, a2=−3, a3=6

wolsztynianka86:

8		3		x + 1
	+		−		pomóżcie
2x + 4		x − 2		x2 − 4

błagam o pomoc!!!!: bardzo prosze o pomoc w tych zadaniach z góry badzo dziekuje osoba które zechcialy mi pomóc oraz prosze o dokładne działania 1)dane sa wielomiany 2) Rozłóż wielomiany na czynniki wykonaj działania a) w(x) = 2x³−3x² w(x) = −3x²+2x²+5x − 1 b) w(x)= 3x⁵ −6x⁴ + 3x³ p(x)= 2x² + 3x q (x)= x⁴ −2x³+4x²− 7 a) w(x) − p(x) b) p(x) razy q(x)

Jasne xD: ↑ STRONKA!

homar: proszę rozwiążcie to..: Rozłóż wielomian w(x)=x3−2x2−4x+8 na czynniki...

homar: proszę rozwiążcie to..: Dane są wielomiany:w(x)=2x3+3x2−4 i p(x)=x−1.Oblicz w(x)*p(x) i podaj stopień nowo otrzymanego wielomianu.

Stefanprawiebatory: Dzięki panu, pomaga pan przy nie jednym sprawdzenie (:

kasia: mam pytanie. Czy jesli rozkładam wielomina na czynniki metodą grupowania to jesli mi wyjdzie powiedzmy: x³(x−1)+2(x−1)+1(x−1) to czy dane czynnik (x−1) moge redukować do jendego nawiasu? powstaloby: (x−1)(x³+2+1) Prosze o szybką odp.

MaT12: Treści zamieszczone na serwerze wystarczą do matury rozszerzonej? Czy jednak trzeba szukać dalej?

Jakub: Strona matematyka.pisz.pl to dobry początek nauki do matury rozszerzonej. Jednak do porządnego przygotowania lepiej kupić kilka zbiorów zadań i rozwiązywać, rozwiązywać, rozwiązywać ...

Mimi: Witam Czy ktoś jest w stanie odpowiedzieć mi na pytanie: Czy na maturze podstawowej obowiązuje mnie dzielenie wielomianów? Na każdej str. internetowej piszą inaczej... Z góry dziękuję

Jakub: Na podstawie nie ma dzielenia wielomianów. Nie kieruj się co jest napisane na różnych stronach w necie, tylko tym co jest w oficjalnym informatorze maturalnym http://www.cke.edu.pl/164-egzamin-maturalny.html

Hubert: pomoże ktoś w tym zadaniu znajdź takie liczby a i b dla których wielomian 6x⁴−7x³+ax²−3x+2 jest podzielny przez trójmian x²−x+b nie wiem jak je zrobić

Krzychu: Pomocy! Dany jest wielomian W(x) = 3x² − 2x² − 5x + 1 Oblicz: W(−1) − 3W (0) −−−−−−−−−−−−−−−− W(√2)

paulina96: Witam. Bardzo proszę o sprawdzenie rozwiązania zadania o następującej treści: Zapisz wyrażenie w postaci sumy algebraicznej (x−3)²−(x²−3)² i oblicz jego wartości dla x= −1. (x−3)²−(x²−3)² (x−3)(x+3)−(x⁴−9)=x²+3x−3x−9−x⁴−9=x²−x⁴ x=−1 (−1)²−(−1)⁴=1−1=0 Z góry dziękuję.

portobello: Witam mam takie równianie jak poniżej mogłabym prosić o jego rozwiązanie bo mi wychodzi za każdym razem inny wynik i sama juz nie wiem który jet dobry oto rowanie: 0,8L*(L−0,22)*[(1+1,5*(0,8L/L−0,22))*14,3*15,5*1*0,9 + (1−0,25*(0,8L/L−0,22))*5,2*15,5*(L−0,22)*0,88] z góry dziękuję za odpowiedź

majkaa1133: PROSZĘ KOCHANI POMURZCIE ! PLIIISSS... b) 4x3 + x2 − 16x − 4 = 0 c) x3 + 5x2 + 6x = 0 d) x³ + 5² + 6x=0

Kuba: Przepraszam serdecznie, al potrzebuję pomocy. Jak liczy się zadania typu f(x)=ax³+bx+c.?

głodny: W sumie to strona się kompletnie nie przydaje dla uczniów klasy rozszerzonej z matematyki. Nie ma tu żadnych wskazówek do zadań z wielomianów jakie znajdziemy z zbiorach zadań wydawnictwa Krzysztof Pazdr sp z.o.o (klasa 2 rozszerzenie).

Jakub: Jakieś konkrety? Jakiego typu zadań tu nie ma?

Norbert: b) 4x³ + x² − 16x − 4 = 0 x²(4x+1) − 4(4x+1)=0 (rozkład wielomianu na czynniki metodą grupowania wyrazów) (4x+1)(x−2)(x+2)=0 Dokończ c) x³ + 5x² + 6x = 0 Wyciągnij x przed nawias x(x²+5x+6)=0 x=0 lub x²+5x+6=0