Gustlik: Jakubie, jeżeli mozesz, to zamieść informację, że prawdopodobieństwo całkowite zazwyczaj stosuje soę do doświadczeń dwu− i więcej etapowych, można zastąpić ten wzór drzewkami, wtedy jest przejrzyściej.*****

Jakub: Sama informacja niestety nie wystarczy. Przydałyby się przykłady. Dodałem do rzeczy, które mam do dopisania.

Jotto: Czy we wszystkich tych wzorach między literką A i B_n jest ukośna kreska czy pionowa? jeśli pionowa, to co oznacza?

Jakub: Ta pionowa kreska oznacza prawdopodobieństwo warunkowe. Ukośna oznaczałaby różnicę zbiorów A i B_n. Zobacz 1020

Wujo: Przydałyby się opisane drzewka i zadania. Dużo ludzi odwiedzą tę stronę, a teraz lipa z p. całkowitym.

Yoda: prosimy o 3−4 zadania do tego podrozdziału, wzorem Bayensa da się zastąpić krzaki, na rozszerzeniu się przyda np 3−4 zadania które da się zrobić z ominięciem tego wzoru, ale jego użycie znacznie ułatwia życie i skraca czas rozwiązania

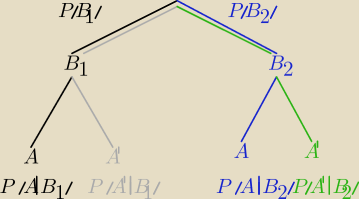
Gustlik: I to jest ten dział, gdzie przydają się drzewka. Zapis np. P(A|B₁) oznacza prawdopodobieństwo warunkowe, czyli prawdopodobieństwo zajścia zdarzenia A, gdy wiemy, że zaszło B₁. P(A)=P(A|B₁)*P(B₁)+P(A|B₂)*P(B₂) Podobnie możemy obliczyć P(A') P(A')=P(A|B₁)*P(B₁)+P(A|B₂)*P(B₂) Jak widać, pozwalaja one nie tylko szybko obliczyć prawdopodobieństwo całkowite, ale też obliczyć, a właściwie odczytać prawdopodobieństwa warunkowe. A także łatwiej jest skorzystać ze wzoru Bayesa w celu obliczenia np. P(B₁|A).

	P(A|B1)*P(B1)
P(B1|A)=
	P(A)

P(A|B₁) i P(B₁) odczytujemy z drzewka i mnożymy (po prostu cała jedna "gałąź"), a potem dzielimy przez prawdopodobieństwo całkowite zajścia zdarzenia A. W prawdopodobieństwie całkowitym, czyli do doświadczeń dwu− i więcej etapowych (np. losowanie urny a potem kuli z urny) drzewka dają obraz tego, co liczymy i są one tutaj świetną metodą. Natomiast stosowanie drzewek (czyli prawdopodobieństwa całkowitego) do zadań z rzutem dwiema kostkami czy trzema monetami (co robi się piorunem regułą mnożenia) czy losowaniem trzech kart z talii 52 kart (co robi się szybciej symbolem Newtona) wygląda jak montaż bomby atomowej w celu zabicia muchy. I w dodatku takie zadania za pomocą drzewek robi się dłużej.

Gustlik: Wkradł sie mały chochlik. Ma być: P(A')=P(A'|B1)*P(B1)+P(A'|B2)*P(B2) Zapomniałem dać "primów". Po prostu jak się kopiuje całe równanie, to można czasem coś zgubić.

Kalafior: ∪, ∩ − co to oznacza ?

Jakub: Zobacz stronę 1059.

aljarah: dlaczego wzór na p. całkowite wygląda jak wygląda? B_n się przecież skraca, więc mamy P(A)=P(A∩B₁)+P(A∩B₂)+...

Jakub: Nic się nie skraca. A|B₁ to nie jest A dzielone przez B₁, tylko prawdopodobieństwo warunkowe. https://matematykaszkolna.pl/strona/1020.html

aljarah: przypomniało mi się to pytanie.. jak to się nie skraca?

	P(A∩B)
P(A|B)=		więc P(A|B)*P(B) = P(A∩B)....
	P(B)