Gustlik: Wzór P(A U B) = P(A) + P(B) − P(A B) (U − suma, − iloczyn zbiorów, napisałem tak, bo nie mogę znaleźć odpowiednich symboli ani sposobu na ich napisanie) można wyprowadzić z interpretacji geometrycznej: narysować dwie nachodzące na siebie figury geometryczne, np. dwa prostokąty. Wówczas pole całej figury (będącej sumą figur A i B) będzie równe sumie pól obu figur pomniejszonej o pole ich części wspólnej, aby nie uwzględnić jej dwa razy.

Jakub: Ja zwykle stosuję: u − suma zbiorów n − iloczyn zbiorów Te litery są wystarczająco podobne do właściwych oznaczeń.

Mastah: Mam pytanie, jeżeli P(∅)=0 a P(Ω)=1 to P(A) nie powinny być 0 ≤ P(A) ≤ 1 ?

Jakub: To co napisałeś jest prawdą. Na początku masz definicję prawdopodobieństwa i w niej masz, że P(A) ≥ 0. Niżej są własności i tam jest napisane, że P(A) ≤ 1. Tą własność da się wyprowadzić z definicji i w sumie to prawie wyprowadziłeś. W definicji nie może, być pełna wersja 0 ≤ P(A) ≤ 1, ponieważ DEFINICJA to coś takiego, co zawiera tylko MINIMALNY zestaw warunków, czyli w naszym wypadku tylko P(A) ≥ 0. Wszystko inne, co się da wyprowadzić nie umieszcza się w definicji.

Paulina: Proszę o pomoc z zadaniem: Wykaż że P(∅)=0. Jak można to wykazać?

Ja: ∅∩Ω=∅ Z aksjomatów wynika, że: P(Ω)=1 oraz dla zdarzeń rozłącznych (wykluczających się) A₁, A₂, ... P(A₁ ∪ A₂ ∪ ... ) = P(A₁)+P(A₂)+... Można więc rozpisać pierwsze równanie na: 1=P(Ω)=P(∅ ∪ Ω)=P(∅)+P(Ω)=P(∅)+1 stąd wynika: P(∅)=0

Semir: To na pewno jest na poziom podstawowy, ja nie miałem tego w szkole.

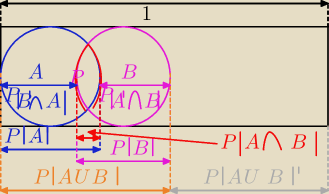
Gustlik: Opracowałem fajny diagram pozwalający zobrazować i szybko obliczać prawdopodobieństwa zdarzeń, gdy dane jest np. P(A) i P(B). Cały prostokąt to Ω, czyli P(Ω)=1. Oczywiście zamiast P(A), P(B) P(AUB) itp. nanoszę na diagram wartości tych prawdopodobieństw, a resztę obliczam "geometrycznie" i potem dorysowuję odpowiednie "strzałki" i nanoszę na rysunek każde obliczone prawdopodobieństwo, np. P(A∩B')=P(A)−P(A∩B). Zbiory rysujemy tak, żeby zbiór A był styczny do lewego boku prostokąta Ω. Na − przed narysowaniem diagramu początku należy sprawdzić dwie rzeczy: czy P(AUB) jest równe 1 czy mniejsze, jeżeli będzie równe 1. Jeżeli będzie równe 1, to oba zbiory "wypełnią" cały prostokąt i nie będzie "luki" z prawej strony. Jeżeli P(AUB)<1, to bedzie ta "luka" i diagram moze wyglądać jak na powyższym rysunku. Jeżeli zbiory nie będą miały części wspólnej, to nie będą nachodzić na siebie, czyli rysujemy je jak okręgi styczne zewnętrznie. Po prostu będą leżały obok siebie stykając się tylko ze sobą. Ta "geometryczna" metoda pozwala na szybkie obliczanie prawdopodobieństw.

Gustlik: Przy tego typu zadaniach przydają się jeszcze prawa de Morgana dla zbiorów: 1. (AUB)'=A'∩B' 2. (A∩B)'=A'UB' Czyli np. P(A'∩B')=P(AUB)'=1−P(AUB) oraz P(A'UB')=P(A∩B)'=1−P(A∩B). Mając więc dane P(A'∩B') łatwo obliczymy prawdopodobieństwo P(AUB), a mając dane P(A'UB') − obliczymy P(A∩B) bez zbędnych kombinacji i bez błędu narysujemy diagram. Warto więc znać prawa de Morgana nawet jeżeli zdajemy tylko matematykę na poziomie podstawowym, bo znacznie upraszczają one rozwiązywanie zadań z własności prawdopodobieństwa.

klaudia: nie wiem skąd to się wszystko bierze . może ktoś wytłumaczyć jakoś po ludzku ?

anon: Jest to chyba część z która będę mieć prawdziwe problemy, ponieważ nie mogę pojąć o co chodzi w aksjomatycznej definicji prawdopodobieństwa. Moje wnioski są dosyć chaotyczne(pewnie będne), ale postaram się przedstawić swój obraz tego, tak aby ktoś mógł mnie poprawić i tym samym pomóc Moje rozumienie tego zagadnienia postaram się zobrazować na rzutach kostką, mianowicie wiele różnych prawdopodobieństw można brać pod uwagę przy żucie taką kostką. Aksjomatyczna definicja prawdopodobieństwa działa na tych prawdopodobieństwach, np. prawdopodobieństwo wyrzucenia liczb parzystych oraz prawdopodobieństwo wyrzucenia liczby 2, te dwa prawdopodobieństwa można zsumować. Tak mi się wydaje iż te działania aksjomatyczne polegają właśnie na działaniach na kilku prawdopodobieństwach. Natomiast tak jak pisałem nie bardzo to rozumiem, a właściwie wydaje mi się iż kompletnie tego nie rozumiem.

Jakub: Aksjomatyczna definicja prawdopodobieństwa opisuje pewną funkcję P. Ma ona pewne własności, które są opisane wzorami. Te wzory i sama funkcja jest pewnym podsumowaniem wszystkiego co wiemy o prawdopodobieństwie, tyle że w praktyce tych wzorów się nie stosuje do rzeczywistych zadań. Chodzi mi o to, że licząc praktyczne zadania np. rzut kostką itd. korzystasz z tego 1019, 1016, 1012, 1013, 1015. Wzory z aksjomatycznej definicji prawdopodobieństwa przydają się rzadko w takich 1748 praktycznych zadaniach. Przynajmniej w zadaniach licealnych. Tak więc zapomnij o praktycznych zastosowaniach aksjomatycznej definicji prawdopodobieństwa. Potraktuj to jako pewne wzory, którymi musisz sprawnie operować. Przykłady zadań masz na 1747. Tylko plizzz nie zadawaj często słyszanego przeze mnie pytania. A po co mi to w życiu? Po nic. Dla samej przyjemności główkowania nad abstrakcyjnymi problemami. Aha. Nie traktuj tych wzorów jako zupełnie nieprzydatnych w praktycznych zadań. Czasami się przydają, tylko na początek lepiej o tym zapomnieć i skupić się tylko na nauce sprawnego ich przekształcania.

anon: Dziękuję za szybkie odpisanie, nie rozumiałem o co w tym chodzi

anonim: "⊂" co oznacza ten symbol ?

Jakub: A ⊂ B, oznacza, że zbiór A zawiera się w B. Zbiór A jest podzbiorem B. Więcej na 1058 i 1059.