nierówność Ola: rozwiąż nierówności : a) 3(2−x)(x+4)≤0 b)−5(x−2)(1−x)≤0 c)x²+10x+25<0 d)−x²+14x−49≤0 e)(x−3)(2x−5)<4x²−2x−20 f)4x²−1<(2x−1)(x+3)

pomagacz: Olka Słońce, tyle zadań liczyliśmy z innymi i nadal są problemy? (a − b)*(c + d) = a*c + a*d − b*c − b*d (a − b)*(c − d) = a*c − a*d − b*c + b*d [+] * [−] = [−] [+] * [+] = [+] [−] * [−] = [+] ax² + bx + c [>, ≥, <, ≤] 0 ax² + bx + c = 0 Δ = b² − 4*a*c jeżeli Δ > 0

	−b ± √Δ
x1/2 =
	2a

jeżeli Δ = 0

	−b
x0 =
	2a

jeżeli Δ < 0 x ∊ ∅ Wciąż to samo robimy, zrób sobie zrzuty ekranu (przycisk [Print Screen], otwierasz Paint, wklejasz [Ctrl]+[C], zapisujesz [Ctrl]+[S] w folderze o nazwie "Zadania z forum", który tworzysz na pulpicie) i otwierasz te obrazki i patrząc na nie starasz się liczyć te zadanka

pomagacz: Oczywiście najpierw szukasz te zadanka które wcześniej nam pokazałaś, najeżdżasz na odpowiedzi i wtedy robisz to: (przycisk [Print Screen], otwierasz Paint, wklejasz [Ctrl]+[C], zapisujesz [Ctrl]+[S] w folderze o nazwie "Zadania z forum")

pomagacz: wszystko co masz w zadaniu przekładasz na lewo, ale pamiętaj o zmianie znaku, a po prawej stronie masz 0, wymnażasz wszystko i liczysz z Δ, te warunki (jeżeli Δ > 0, jeżeli Δ = 0, jeżeli Δ < 0) sprawdzasz, który odpowiada wyliczonej Δ i obliczasz miejsca zerowe, jeżeli warunek na to pozwala. Następnie rysujesz parabolę dla funkcji kwadratowej, byle jaką, ale pamiętaj: jeżeli a > 0 to ramiona w górę jeżeli a < 0 to ramiona w dół https://matematykaszkolna.pl/strona/79.html https://matematykaszkolna.pl/strona/93.html i korzystając z tych zapisków policz te zadanka które podałaś przed chwilą: https://matematykaszkolna.pl/strona/1684.html

pomagacz: a) 3(2−x)(x+4) ≤ 0 3(2x + 8 − x² − 4x) ≤ 0 3(−x² − 2x + 8) ≤ 0 −3x² − 6x + 24 ≤ 0 \\*(−1) 3x² + 6x − 8 ≥ 0 ← zmiana symbolu po mnożeniu przez liczbę ujemną Δ = 36 + 4*3*8 = 132 ← jest tak, bo −4*3*(−8) = + 4*3*8 zasada [−] * [−] = [+] √132

pomagacz: √Δ = √132 = 2√33

	−6+2√33		√33
x1=		= −1 +		←użyłem takiego zapisu, bo jest łatwiejszy w interpretacji
	6		3

	−6 − 2√33		√33
x2 =		= −1 −
	6		3

	√33		√33
x ∊ (−∞, −1 −		> ∪ <−1 +		, +∞)
	3		3

rupert: No niestety, ale koleżankę w błąd wprowadzasz. Prawidłowe wyniki to x₁= −4, a x₂=2

rupert: A ramiona paraboli będą skierowane w dół.

ICSP: z postaci iloczynowej funkcji kwadratowej nie możesz odczytać pierwiastków? Niby po co jest rozkład wielomianu?

krystek: Olu słuchaj Ruperta Masz:3(2−x)(x+4)≤0 masz zaraz miejsca zerowe x=2 ,x=−4 kreślisz parabole ,ramiona w dół (gdybyś wymnożyła masz −3x² czyli a<0) i dczytujesz gdzie masz wartości ≤0 czyli dla x należącego ... i podajesz przedziały.

ICSP: zmienił znak więc ramiona będą skierowane w górę. Nie wiem czemu zamieniłeś z powrotem 24 na 8. Jednak: 3(2−x)(x+4) = 0 ⇔ 2−x = 0 v x+4 = 0 ⇔ x = 2 v x = −4 ramiona są skierowane w dól i odp. 3(2−x)(x+4) ≤ 0 ⇔ x ∊ (−∞;−4> suma <2;+∞)

Ola: mhm więc w przykładzie a) i b) nie muszę liczyć jak mówi pomagacz ? Zrobiłam tak i wb mam dobry wynik x∊<1, 2> zaraz spróbuję następne przykłady sposobem pomagacza...

rupert: Tak, w b mamy x−2=0 v 1−x=0 x=2 v x=1.

Ola: c)x2+10x+25<0 d)−x2+14x−49≤0 spróbowałam liczyć deltę i m. zerowe ale nie taki ma byc wynik jak wychodzi ... a za e)(x−3)(2x−5)<4x2−2x−20 f)4x2−1<(2x−1)(x+3) kompletnie nie wiem jak się wziąc

sushi_ gg6397228: c) wzor skroconego mnozenia (a+b)² d) wyciagnij minusa przed nawias i potem wzor (a−b)² e, f) przemnozyc tam gdzie sa nawiasy, potem wszystko na jedna strone

Ola: c) zwinęłam do postaci (x+5)² w odp pisze ze ma być nierówność sprzeczna wiec jest ok ?

Ola: d) −(x²−14x+49) (x−7)² i co dalej ?

Ola: e) (x−3)(2x−5)<4x2−2x−20 2x²−5x−6x+15<4x²−2x−20 2x²−5x−6x+15−4x²=2x+20<0 −2x²−9x+35<o probowalam liczyc delte z tego ale jest ona ujemna

Jack: jesli rachunki są ok, to dla Δ<0 i a<0 jak wygląda wykres takiej funkcji?

Ola: c) zwinęłam do postaci (x+5)2 w odp pisze ze ma być nierówność sprzeczna wiec jest ok ?

Ola: d) −(x2−14x+49) (x−7)² i co dalej ? e) (x−3)(2x−5)<4x2−2x−20 2x2−5x−6x+15<4x2−2x−20 2x2−5x−6x+15−4x2=2x+20<0 −2x2−9x+35<o probowalam liczyc delte z tego ale jest ona ujemna

rupert: Nie szkodzi. Możesz spokojnie liczyć Δ oraz x₁ i x₂.

sushi_ gg6397228: −(x−7)²≤0 masz jedno miejsce zerowe−−> jak wyglada rysunek dla ułatwienia (x−7)² ≥0 e) Δ wychodzi dodatnia

Ola: d) ma wyjść xeR a z c) co zrobić dalej jak mam (x+5)²

krystek: Pomyśl Olu ,masz kwadrat liczby ,który jest zawsze dodatni więc nie spełnia go żadna liczba x.jak narysujesz parabolę nie masz miejsc zerowych ,gałęzie skierowane w górę i przyjmuje tylko wartości dodatnie ponieważ leży nad osią OX . Ty masz właśnie taką nierówność rozpatrzyć (x+5)²>0

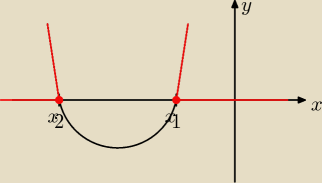
Anna: c) (x+5) < 0 ⇔ x ∊∅ (brak rozwiązań, nierówność sprzeczna) (parabola nie przyjmuje wartości ujemnych)

Anna: Pomyłka: tam ma być oczywiście: (x+5)² < 0

krystek: A ja przepraszam ,że względu na późna porę objaśniłam x²+5>0

Ola: więc jak ma w końcu być

Ola: e) (x−3)(2x−5)<4x2−2x−20 2x2−5x−6x+15<4x2−2x−20 2x2−5x−6x+15−4x2=2x+20<0 −2x2−9x+35<o nie wiem to jest dobrze licze Δ, ale nadal mam ujemną nie wiem co dalej

rupert: (x+5)²<0 x+5=0 x=−5 Wykres jest taki, jak Anna narysowała. Po prostu chodziło o znak < aby był w prawidłową stronę.

Ola: d) ma wyjść xeR

krystek: Olu w d)−x²+14x−49≤0 Δ=0 i otrzymujesz −(x−7)²≤0 gdzie jedynym m zerowym jest x=7 i jak narysujesz wykres gałęzie skierowane w dół widzisz ,że spełnione dla xeR

Norma: i co zrobić z e)