promien patriko: oblicz promien okregu opisanego na trojkacie rownobocznym wiedzac ze wysokosc wynosi h =2 √3

asd: h = 2√3 jest to trójkąt równobyoczny więc jest dla tego zależność że promień okręgu opisanego = R R = ²₃h R = ²₃ * 2√3 = ⁴₃√3. gdyby nie był to trójkąt równoboczny to korzystamy z wzorów innych −−−> 541 jak masz jakieś pytania, albo czegoś nie rozumiesz to pytaj.

patriko: oblicz pole trojkata rownoobocznego wna ktorym opisano okrag o promieniu R =√3 to zadanko

patriko: okrag o promieniu1 cm jest wpisany w trojkat rownoramienny o podstawie 4cm oblicz dlugosc ramienia trojkata bardzo dziekuje

asd: pierwsze. Mamy obliczyć pole trójkąta. Są dwie możliwości (tak jak na rysunku) że albp na trójkącie jest opisany okrąg (wtedy chodzi o ten duży) lub w trójkąt jest wpisany okrąg (mały) R − promień dużego okręgu tego który jest opisany, natomiast r − promień małego okręgu, tego wpisanego w trójkąt. pamiętajmy, że R = ²₃h, i r = ¹₃h, gdzie h jest wysokością. Jeszcze przydadzą się wzory −−−−−−> 856. pierwsza możliwość − okrąg opisany na trójkącie R = √3 = ²₃h, więc h = √3 * ³₂ = ^3√3₂ teraz mając wysokośc trójkąta możemy policzyc jego bok. h = ^a√3₂ = ^3√3₂ widać, ze a=3 i teraz jak mamy bok (a) to możemy ze wzoru policzyć pole P − Pole = ^a2√3₄ = ^9√3₄ <−−−−Pole dla okręgu opisanego. teraz policzmy drugi przypadek, gdyby okrąg był wpisany, wtedy r= √3 = ¹₃h h= 3√3 i liczymy tak jak wcześniej bok (a) a później pole (p). ^a√3₂ = 3√3 a√3 = 6√3 a=6 P = ^a2√3₄ = ^36p[3}₄ = 9√3. Czyli popatrz. promień w obu przypadkach jest jednakowy, gdyby koło było na zewnątrz trójkąta to musiałby być mniejszy (ten trójkąt), niż w przypadku gdy okrąg znajduje się w środku (wtedy tójkąt jest większy, bo musi pomieścić w środku okrąg). Wychodzi nam że pole większego jest czterokrotnie większe.

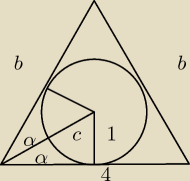
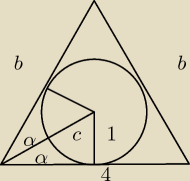asd: dosyś skomplikowane zadanie. policzmy najpierw długosć "c" c² = 1¹ + 2² = 5 c = √5 teraz sin cos tg i ctg dla α sinα = ¹_√5 = ^√5₅ cos = ²_√5 = ^2√5₅ tg = ¹₂ ctg = 2 teraz ze specjalnego wzoru policzby cos 2α i do bedzie ten kąt między podstawą a ramieniem trójkąta . cos2α = 1 − 2sin²α = 1 − ¹⁰₂₅ = ¹⁵₂₅ zauważmy teraz, że cos2α = ²_b = ¹⁵₂₅ b = ⁵⁰₁₅ = 3¹₃ Odp.: Ramiona mają po 3¹₃ [cm].