trapez Daria: Pole trapezu prostokątnego jest równe 26 cm. jego wysokosc jest o 1 cm krótsza od jednej i o 4 cm krótsza od drugiej podstawy. oblicz obwód

Daria: witam czy ob= 12 + √73

Daria: prosze o sprawdzenie bardzo prosze nie jestem pewna

Daria: proszę o sprawdzenie bo naprawde nie jestem pewna swoich obliczeń

Daria: i jak myślicie dobrze?

Daria: prosze o odp

kamis: P_trapezu = 26 Wprowadźmy oznaczenia: x − długość krótszej podstawy y − długość dłuższej podstawy x, y > 0 i y > x H − wysokość trapezu Ze wzoru na pole trapezu

	x + y		x + y
Ptrapezu =		* H ⇒ 26 =		* H
	2		2

Z treści zadania: H ⇒ x − 1 = y − 4 y = x + 3 Podstawiając do wzoru w miejsce H = x − 1 i y = x + 3

	x + x + 3
26 =		* (x − 1)
	2

	2x2 − 2x + 3x − 3
26 =
	2

52 = 2x² + x − 3 2x² + x − 55 = 0 √Δ = 21

	−1 + 21
x1 =		= 5
	4

	−1 − 21		11
x2 =		= −		− odrzucamy to rozwiązanie, gdyż długość boku nie może być
	4		2

wyrażona liczbą ujemną Długość krótszej podstawy − 5 Długość dłuższej podstawy − x + 3 = 5 + 3 = 8 Długość wysokości − x − 1 = 5 − 1 = 4 Długość ramienia − 5 (obliczasz z twierdzenia Pitagorasa) Obwód = 5 + 5 + 4 + 8 = 22

Daria: ja inaczej zrobilam ptrapezu = 26 p=(a+b) h /2 a= h+2 b=h+4 p=(h+1 + h+4)h/2 p= (2h +5)h/2 p= 2h² + 5h /2 26 * 2 = 2h² + 5h 0= 2h² + 5h − 52 delta = 441 x1= 8 x2= − 13 − odpada twierdzenie pitagorasa 8²+ 3²= r² czyli r= √73 ob = 29 + √73

Daria: poprawa a = h+1

Daria: kamis jak myslisz?

kamis: Pomyliłaś się przy liczeniu pierwiastków

	−5 + 21		16
x1 =		=		= 4
	4		4

Sposób jest dobry, tylko błąd w obliczeniach

Daria: zwracam honor pomyłka w obliczeniu x1

Daria: i wszystko sie zgadza kamis sprawdz jeszcze to https://matematykaszkolna.pl/forum/95146.html

234: wpisz To otrzymasz 7⁵ 75 11² 112 x³ + x² + x + 1 x3 + x2 + x + 1 5¹⁰ 510 8^2x−1 + 4^x = 2 82x−1 + 4x = 2 2²⁰⁰⁹ 22009 64 = 8² = (2³)² = 2^3*2 = 2⁶ 64 = 82 = (23)2 = 23*2 = 26 3⁴⁵ 345 5^x2−2 5x2−2 x^x2 = e^{ln xx2} = e^x2lnx xx2 = eln xx2 = ex2lnx √3 √3 √121 √121 ³√8 3√8 ⁴√625 4√625 3 ^√2 3 √2 ²₃ 23 1⁴₅ 145 ²₇ + ³₇ = ⁵₇ 27 + 37 = 57 (1²₃ − 2⁷₈) * ⁴₅ (123 − 278) * 45

1		2		4
	+		− 1
2		3		5

1 2 4 + − 1 2 3 5

3x − 2
2x + 1

3x − 2 2x + 1

2 + 12
13 − 45

2 + 12 13 − 45

3 + 14   2 +   7 − 89
5

3 + 14 2 + 7 − 89 5

8 5

nawias 8 nawias nawias 5 nawias

9 4		9!
	=
		(9−4)!*4!

nawias 9 nawias nawias 4 nawias 9! = (9−4)!*4!

⎧	x+y=5
⎩	x−y=3

⎧ x+y=5 ⎩ x−y=3

⎧	x=3
⎨	y=4
⎩	z=6

⎧ x=3 ⎨ y=4 ⎩ z=6

	⎧	x gdy x≥0
|x| =	⎨
	⎩	−x gdy x<0

⎧ x gdy x≥0 |x| = ⎨ ⎩ −x gdy x<0 Wzory są na stronie 55 Wzory są na stronie 55 Rozdział z wielomianów jest tutaj i8 Rozdział z wielomianów jest tutaj i8 Na forum było już to zadanie tutaj 12318 Na forum było już to zadanie tutaj 12318 podkreślony, pogrubiony podkreślony, pogrubiony czerwony, czerwony czerwony, czerwony niebieski, niebieski niebieski, niebieski zielony, zielony zielony, zielony fioletowy, fioletowy fioletowy, fioletowy brązowy, brązowy brązowy, brązowy szary, szary szary, szary :(( :( tiaaa <je_pizze> > ]

Gustlik: Pole trapezu prostokątnego jest równe 26 cm KWADRATOWYCH !. jego wysokosc jest o 1 cm krótsza od jednej i o 4 cm krótsza od drugiej podstawy. oblicz obwód W zadaniach, gdzie dane są wielkości, które zazwyczaj się oblicza, jak pole czy objętość, stosujemy zasadę "co masz dane, to obliczasz". 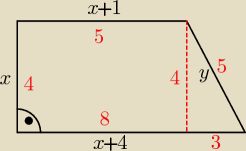Zasada polega na obliczeniu danej wielkości za pomocą niewiadomych, przyrównaniu jej do wartosci podanej w zadaniu i rozwiązaniu tak otrzymanego równania, czyli w tym przypadku musimy obliczyć pole tego trapezu z boków stosując oznaczenia na rysunku, bo pole jest dane:

	(x+4+x+1)*x		(2x+5)*x
P=		=
	2		2

Teraz przyrównujemy to pole do wartości podanej w zadaniu i mozemy je rozwiązać NA JEDNEJ NIEWIADOMEJ:

(2x+5)*x
	=26 /*2
2

(2x+5)*x=52 2x²+5x−52=0 Δ=441, √Δ=21 x₁=−6,5 − odpada, x₂=4 Teraz z Pitagorasa oblicz y, powinno wyjśc 5 i zsumuj boki.