GAZETA WYBORCZA 27 kwiecień 2011 Vizer: GAZETA WYBORCZA 27 kwiecień 2011 Poziom rozszerzony z matematyki. Podam zadanka dla zainteresowanych maturą rozszerzoną maturą z matemtyki, które ukazały się dzisiaj w Gazecie Wyborczej. zad.1 Rozwiąż nierówność |x+2|+|3x−9|>23 zad.2 Wyznacz, wszystkie wartości parametru m, dla których równanie x²−mx+1=0 ma dwa różne pierwiastki rzeczywiste x₁, x₂ takie, że x₁³+x₂³>m²+m−4 zad.3 Wyznacz wszystkie wartości parametru m, dla których wykres wielomianu W(x)=x⁵−2x⁴−2mx³+4mx²+m²x−2m² ma dokładnie dwa punkty wspólne z osią OX. zad.4 Wykaż, że dla każdych dodatnich liczb rzeczywistych a,b,c,d prawdziwa jest nierówność √(a+c)(b+d)≥√ab+√cd zad.5 Rozwiąż równanie cos2x +√3*sin2x=cos²x−7sin²x zad.6 Trzy liczby, których suma jest równa 26, są jednocześnie trzema kolejnymi wyrazami ciągu geometrycznego oraz drugim, trzecim i szóstym wyrazem rosnącego ciągu arytmetycznego. Wyznacz te liczby. zad.7 Oblicz, ile jest wszystkich liczb naturalnych sześciocyfrowych, w zapisie których występuje dokładnie raz cyfra 1, oraz dokładnie dwa razy cyfra 2. zad.8 W trójkącie prostokątnym ABC odcinek CD jest wysokością opuszczoną na przeciwprostokątną AB. Obwód trójkąta ADC jest równy 40, a obwód trójkąta BDC jest równy 24. Oblicz obwód trójkąta ABC. zad.9 Długości przekątnych rombu o kącie ostrym 45(st.) są równe e oraz f (e<f). Wykaż, że

e
	=√2−1
f

zad.10 Punkty A=(9,12) oraz B=(5,10) leżą na okręgu, którego środek leży na prostej o równaniu x+y+3=0. Wyznacz równanie tego okręgu. zad.11 Dany jest zbiór trójkątów równoramiennych o obwodzie 24. Oblicz długości boków trójkąta należącego do tego zbioru, który przy obrocie dookoła prostej zawierającej jego podstawę o kąt 360(st.) wyznacza bryłę o największej objętości. Uff przepisałem, życzę powodzenia w rozwiązywaniu.

Kejt: o, dziękuję. Właśnie miałam zamiar zrobić to samo

K+K: czy w pierwszym zadaniu wyjdzie przedział (−∞; −2) ∪(6;+∞)

Vizer: Nie próbuj dalej

K+K: dzieki

K+K: a jakbyś to rozwiązał

Vizer: Rozpatrzyłbym standardowo przypadki I. (−∞,−2) II.<−2,3) III.<3,+∞)

K+K: kurcze ja też to musiałam się gdzieś pomylić

;):

	15
W pierwszym mi wyszło x∊(−∞,−4)∪(		,∞)
	2

kamis: Najciekawszym wydaje się być zadanie numer 7.

;): 2 też zrobiłem pomyślę sobie nad 3 zadaniem

K+K: kurde faktycznie pozjadałam minusy ale ze mnie gapa

Vizer: kamis dokładnie tak nam powiedział nauczyciel z matmy ; ) Dobrze Ci wyszło

;): Okej dzięki Vizer a w 2 zadaniu m∊(2,∞)?

Vizer: Tak zgadza się.

rumpek: W dzisiejszej gazecie były też od razu odpowiedzi ?

;): 3 za chwilkę zrobię w 4 mogę tak zrobić? √(a+c)(b+d)≥√ab+√cd /² ab + ad + cb + cd ≥ ab + 2√abcd + cd ad − 2√abcd + cb ≥ 0 (√ad − √cb)² ≥ 0

Vizer: Tak dzisiaj sobie zrobiłem maturkę w domu robię tak co dwa tygodnie od lutego gdzieś, czyli o 9:00 podstawa i 14:00 rozszerzoną i dzisiaj sobie tą zrobiłem.

rumpek: Możesz zrobić zdjęcie albo zeskanować ? Bo chyba trochę męczące jest podawanie wyników a tak można sobie sprawdzić od razu.

Vizer: No w sumie nie wiem czy można tak zrobić w odpowiedziach jest (ad+bc)²≥0, bo trzeba było drugi raz podnieść do kwadratu.

;): rumpek 1 i 2 mam Ci napisać?

Vizer: ok już piszę

;): Ale skoro liczby a,b,c,d są dodatnie to chyba można tak zrobić czy nie?

Monika: Przepraszam, że nie w swoim temacie. Ale mogli byście mi pomóc ? https://matematykaszkolna.pl/forum/93379.html Nie wiem czy dobrze zrobiłam z tym t

Vizer: ad.1 (−∞,−4)∪(7,5;+∞) ad.2 m∊(2,+∞) ad.3 m₁=0, m₂=4 ad.4 dowód ( na końcu dojść do (ad−bc)²≥0)

	5
ad.5 (x=kπ v x=		π+kπ) ∧ k∊C
	6

ad.6 Liczby 2, 6 i 18 ad.7 28800 ad.8 8√34 ad.9 dowód ad.10 o: (x−28)²+(y+31)²=2210 ad.11 podstawa ma długość 6, ramiona mają długość 9

Wojteq66: Odnośnie zad4: mnie wyszło coś takiego, jest to dopuszczalne czy nie bardzo? (ad − cb)² ≥0

Vizer: ; ) gdybym ja był egzaminatorem to bym Ci pewnie zaliczył

Wojteq66: dzięki Vizer

;): Właśnie pewnie bym musiał jeszcze uzasadnić że a,b,c,d są dodatnie więc zachodzi taka nierówność dla liczb rzeczywistych dodatnich

kamis: Masz w treści zadania podane: Wykaż, że dla każdych dodatnich liczb rzeczywistych a,b,c,d

;): 3 udało mi się zrobić chociaż początkowo w ogóle nie miałem pomysłu jak dojść do rozwiązania

;): kamis wiem tylko mówię że na maturze dla egzaminatora by nie wystarczyło to i bym musiał słownie dać komentarz

Monika: A jak zrobiłeś to 3? Mógłbyś tutaj je zrobić ?

romanooo: a skąd masz że m =4 , nie powinno być m≥0 w tym 3 zadaniu ?

Monika: To zrobicie to 3 , proszę

;): W(x) = x⁴(x − 2) −2mx²(x − 2) +m²(x − 2) W(x) = (x − 2)(x⁴ − 2mx² + m²) W(x) = (x − 2)(x² − m)² Jeżeli ma dokładnie dwa punkty wspólne z OX to ma dokładnie 2 miejsca zerowe m = 0 mamy W(x) = x⁴(x − 2) dla m = 4 W(x) = (x − 2)(x + 2)²(x − 2)² W(x) = (x − 2)³(x + 2)

romanooo: W(x)= x⁴(x−2) − 2mx²(x−2)+m²(x−2) W(x)=(x⁴−2mx²+m²)(x−2) Wielomian ma mieć 2 punkty wspólne czyli 2 pierwiastki. jeden już mamy niezależnie od x−2

romanooo: ufff miałem przeczucie że ktoś to robi

Monika: Skąd tam wziąłeś m = 0 i m = 4?

romanooo: ale jak znalazłeś/aś że m = 4. bo podstawić zawsze można...

Artur: mam tą gazetkę, jeśli chcecie mogę wam wrzucić odpowiedzi do zadań z etapami rozwiązań tak jak jest to podane w wyborczej

;): Jak skąd? Dla m = 0 mamy dwa pierwiastki 0 −4krotny i 2 a dla m = 4 mamy 2 pierwiastki 2 − 3krotny i −2 − 2krotny

romanooo: no dobra, jak możesz to napisz z 3 ten fragment już po zapisaniu wielomianu w postaci iloczynowej

Monika: Jakbyś mógł to wrzuć byłabym wdzięczna

Vax: 3) x⁵−2x⁴−2mx³+4mx²+m²x−2m² = x⁴(x−2)−2mx²(x−2)+m²(x−2) = (x−2)(x⁴−2mx²+m²) = (x−2)(x²−m)² = (x−2)(x−√m)²(x+√m)² Mamy już jeden zapewniony punkt wspólny o osią OX dla x=2, aby dany wielomian miał dokładnie 2 miejsca zerowe musi zachodzić: x−2 = x−√m v x−2 = x+√m v x−√m = x+√m Z pierwszego mamy m=4, drugie jest sprzeczne a z 3 m=0 więc dany wielomian ma 2 punkty wspólne z osią OX jedynie dla: m ∊ {0 ; 4} Pozdrawiam.

romanooo: ; ) no dobra, wiem że tak to ma być ale masz zrobić tak żeby m wyliczyć, a nie podstawić

romanooo: Vax dzięki

;): To jak byś mógł to od razu było by lepiej sprawdzać gdzie się machnął ktoś Znalazłeś bo dla m < 0 mamy postać W(x) = (x − 2)(x² + m)² więc ma tylko jeden pierwiastek Dla m ≥ 0 W(x) = (x − 2)(x² − m)² W(x) = (x − 2)(x + √m)²(x − √m)² więc żeby były dwa pierwiastki z czego jeden już mamy 2 to chyba nie jest trudno znaleźć

Monika: Ale skąd ta 4 i 0, moglibyście krok po kroku napisać ?:( nie rozumiem tego typu zadań

;): Vax jeszcze lepiej ode mnie wytłumaczył więc spójrz u niego skąd te 0 i 4

Vax: Mamy 3 przypadki: 1) x−2 = x−√m 2) x−2 = x+√m 3) x−√m = x+√m 1) Tutaj mamy √m = 2 ⇒ m=4 2) Tutaj mamy √m = −2 co jest niemożliwe, ponieważ pierwiastek z dowolnej liczby rzeczywistej jest nieujemny. 3) √m = −√m co zajdzie ⇔ m = 0 Stąd otrzymujemy m ∊ {0 ; 4} Pozdrawiam.

Artur: 1)http://iv.pl/images/54887299400263373322.jpg 2)http://iv.pl/images/51774382484342888521.jpg 3)http://iv.pl/images/62094177208469807039.jpg 4)http://iv.pl/images/74414545649256453299.jpg Prosze Monia Tylko ma przestudiować dokładnie aa i jakiegoś buziaka w podziękowaniu

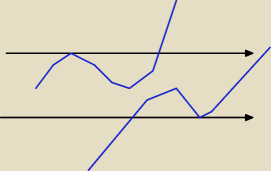
Vizer: Może nie wiesz na czym polega, żeby miał dwa punkty wspólne z osią OX, na rysunku przedstawiłem dwie możliwości

Monika: Dziekuje wam

Rivi: Mi coś w 8 nie wychodzi, inne si... Jakaś podpowiedź? merdają mi się te wszystkie odcinki

Rivi: o, dziekuję

Monika: Ok, już wiem skąd te m = 4 i m = 0, tylko jakbyście mogli mi napisać dlaczego takie przypadki zostały wzięte pod uwagę?

Monika: Podpowie ktoś?

bart: marze o takiej maturce

wafel: nikt wiecej nie komentuje? ; >

szpilka: może jakieś rady dla przyszłorocznej maturzystki? ja się zaczęłam już uczyć żeby nie mieć spiny za rok rozszerzony human pozdrawia a zdaję majce rozsz. będę trzymać za Was kciuki! baaardzo mocno

Vax: Warto zauważyć, że nierówność z zadania 3 jest to spierwiastkowana nierówność Cauchy'ego Schwarza dla 2 ciągów (√a , √c) (√b , √d) Pozdrawiam.

wafel: aha ok ale nic nie zrozumialem

wafel: szpilka UCZ SIE ale tak naprawde a nie ze ci sie wydaje ze sie uczysz ; )

szpilka: wafel, no racja, święta racja mam plan trzaskać regularnie, czyli codziennie, tak z 15−20 zadań z roszerzenia. chyba lepiej tak, niż potem robić wielkie zrywy. jednym słowem: NIEMAOPIERDALANIASIĘ!

wafel: I NIE BEDZIE LIPA

Mordo: Co do zadania 7, to czy liczbą naturalną może być tu zero?

Vizer: Tak też.

Rivi: Tam pracujesz na zbiorach liczb 6cyfrowych, więc zero jako tako nie występuje samo. A w liczbie np 293002 może oczywiście Tylko nie na 1 miejscu

K+K: czy ktoś mógłby mi wytłumaczyć dlaczego w zad 10 pojawia się założenie x∊(0;6) wszystko rozumiem ale sama tego bym nie napisała

K+K: sorki to zad 11 nie 10

Rivi: Ponieważ r²=12(12−2x), a to musi być dodatnie, więc 12−2x>0 x<6 a, że większy od 0 to wiadomo, bo podstawa nie może być <0

K+K: no tak dzięki wielkie

Tomek: kurde nie moge sobie wyobrazić tej figury z zadania 11

K+K:

abc: czy mógłby ktoś wytłumaczyć zadanie nr 7? Najlepiej z zasady mnożenia albo po prostu wyjaśnić, skąd wzięły im się te liczby w kombinacji

Łukasz: ZADANIE 2 To rozumiem (x₁+x₂)(x₁²−x₁x₂+x₂²) Ale tego nie (x₁+x₂)(x₁¹+2x₁x₂+x₂²−3x₁ x₂) Wytlumaczycie jak Oni to podnieśli POMOCY:(

abc: żeby zastosować wzory Viete'a na sumę i iloczyn dwóch pierwiastków, musisz pozmieniać to tak, żebyś te wzory miał. w pierwszym równaniu wszystko grałoby, gdyby nie x₁² + x₂², nie ma takiego wzoru. zapisali więc sumę kwadratów jako kwadrat sumy, ale wtedy (x₁ + x₂)² = x₁² + x₂² + 2x₁x₂, więc za dużo o ten ostatni składnik, który trzeba zwyczajnie odjąć, stąd ostatnie przekształcenie.

abc: nie wiem, czy dobrze wytłumaczyłam, po prostu kwadrat sumy x₁ i x₂ jest o 2x₁x₂ większy niż suma kwadratów x₁ i x₂, więc żeby otrzymać to samo należy odjąć to, czego jest za dużo

Wiwi: To co oni zastosowali to rozszerzenie sobie tej drugiej części.

	coś
Coś jakby pomnożyć wszysto razy		.
	coś

Da to i tak i tak 1. czyli nic się nie zmieni poza zapisem. Zauważ, że : 2x₁x₂−3x₁x₂ =−x₁x₂ . W konsekwencji nic się tam nie zmienia... ale jednak jest to konieczny zabieg do dalszych przekształceń.

abc: aha, a ja oczywiście nie popatrzę dobrze i tłumaczę to, o co w ogóle nie chodziło sorry

Wiwi: Mam pytanie co do zadania 4. Ja to zrobiłem tak (podobnie do nich... ale...) podniosłem do kwadratu itd. . . . . dochodze do takiego momentu: ad+cb≥2√abcd ad+cb−2√abcd≥0 (√ad−√cb)²≥0 no i cokolwiek podniesione do kwadratu zawsze jest większe lub równe 0. Podobnie do ich, tylko ja nie podniosłem drugi raz do kwadratu. Czy mam to dobrze ?

abc: Tak, bo tak jak powiedziałeś każda liczba podniesiona do kwadratu jest ≥ 0. Chyba po prostu trzeba to zapisać słownie i tyle

Rivi:

abc, zad7

na 1) na pierwszym miejscu masz "1" zostaje 5 miejsc − dwie dwójki można na 10 kombinacji. i

zostają trzy miejsca, po 8 cyfr może tam być − 1*10*83=5120

2) na pierwszym miejscu jest "2", jedynka może być na 5 miejscach, kolejna dwójka na 4, i 3 miejsca na 8 cyfr

1*5*4*83=10240

3) na początku masz jedno z 3,4,5,6,7,8,9, potem na jednym z pięciu masz "1", na 4 miejscach masz dwie dwojki − 6 kombinacji. I na dwóch wolnych z 8 możliwych cyfr.

7*5*6*82=13440

razem=28800

Wiwi: A mam pytanie jeszcze do zadania 5. Czy jest tylko ten jeden sposób na jego wyliczenie ? Bo muszę przyznać, że nie wpadłbym na to żeby wprowadzić tam tangensy. zacząłem to robić tak : cos2x +√3sin2x=cos²x−7sin²x 1−sin²x+√32sinxcosx=1−sin²x−7sin²x 2√3sinxcosx=−6sin²x i co dalej z tym? Bo te tangensy mi się nie widzą. Jest coś innego ?

Rivi:

ew można wyciągnąć przed nawias (i podzielić na dwa)

sinx(3sinx+√3cosx)=0 sinx=0 to spoko 3sinx+√3cosx=0 tu w sumie ja bym już podzielił na te cosx 3tgx+√3=0

	√3
tgx=−
	3

chyba na jedno wychodzi w sposobie

kamis:

	π
Przy dzieleniu przez cosx powinieneś chyba postawić założenie: x ≠		+ kπ, k ∊ C
	2

Stare powiedzonko: "Pamiętaj cholero nie dziel przez zero!"

Rivi: tak, tak, domyślnie takie założenie się ustala Tzn, widać w postaci równania, że cosx=0 nie jest rozwiązaniem (i nie wiem, czy za nie napisanie tego słownie, by odjęto punkty, więc lepiej pisac

Wiwi: aha rozumiem. A powiedzcie mi jeszcze co wiecie na temat wysokosci poprowadzonej na przyprostokątną w trojkacie prostokatnym ? Czy ona dzieli tą przyprostokątną w jakimś stosunku czy jak ? Pytam i to w kontekście zadania 8.

abc: Rivi, dzięki za rozwiązanie. co do zadania 8. najlepiej je zrobić z podobieństwa, ale jeśli chodzi o tę wysokość to h²= pierwsza część przeciwprostokątnej * jej druga część

Wiwi: Wytłumaczcie mi to porównanie, bo nie czaje tego... Zad. 8. Tam robią podobieństwo :

b		40
	=
c		p

skoro c to przeciwprostokątna (cała !) to dlaczego tam jest przyrównianie tylko do obwodu trójkąta ADC =40 ?

o_O: Jestes dobry/dobra z matematyki? To mam dla ciebie zadanie: |x| + x > 2 Powodzenia

abc: b to jest przeciwprostokątna tego trójkąta ADC więc przeciwprostokątna małego/przeciwprostokątna dużego = obwód małego/obwód dużego. o to chodzi?

abc: o_O. rozpatrujesz dwa przedziały. 1) x∊ (−oo, 0) tu opuszczasz moduł ze zmianą znaków czyli −x+x>2 0>2 sprzeczność, więc w tym przedziale nie ma rozwiązań 2) x≥0 x+x>2 2x>2 x>1 i z zał. x≥0 czyli w sumie x>1 i to jest odp

Wiwi: No nie może być tak jak mówisz, bo jeśli 'c' jest przeciwprostokątną trojkata ADC to jaki zwiazek ma trojkat BCD z tym wszystkim. Dlaczego podany jest kolejny stosunek :

	a		24
		=		. skoro wg tego co mowisz 'c' nie ma zadnego związku z trójkątem BCD. ?
	c		p

abc: jako c oznaczyli bok AB czyli przeciwprostokątną trójkąta ABC, teraz zarówno trójkąt ADC jest podobny do ABC (cecha KK), jak i DCB do ABC (ta sama cecha). Więc wzięli pod uwagę przeciwprostokątne małych i dużych, ich stosunki są równe stosunkowi obwodów. Z podobieństwa ADC do ABC wyszło, że b/c = 40/p, a z podobieństwa CDB do ABC wychodzi, że a/c=24/p.

małgosia: Dalej nie wiem jak zrobić 7dme Kto pomoże? Chciałam to zrobić regułą mnożenia ale wychodzi mi za dużo możliwości

Wiwi: Małgosiu zerknij na to co Rivi napisał. Bardzo czytelnie zrobił to zadanko. Dzięki abc, ale dalej nie czaje . Zmeczony jestem. Ale obiecuje ze nie spoczne zanim tego nie rozkminie. Ale poradze sobie. Przeczytam 100 razy Twoją wskazówkę i załapię w koncu

Vizer: https://matematykaszkolna.pl/forum/93338.html Tutaj masz to zadanie rozwiązywane przeze mnie i przez sowę.

małgosia: pierwsza cyfra to 9 możliwości {1, 2, 3, 4, 5, 6, 7, 8, 9} druga cyfra to 9 możliwości {0, 2, 3, 4, 5, 6, 7, 8, 9} trzecia cyfra to 8 możliwości {0, 3, 4, 5, 6, 7, 8, 9] czwarta cyfra to 8 możliwości {0, 3, 4, 5, 6, 7, 8, 9} piąta cyfra to 8 możliwości {0, 3, 4, 5, 6, 7, 8, 9} szósta to też 8 {0, 1, 2, 3, 4, 5, 6, 7, 8}

małgosia: co jest nie tak w tym rozumowaniu ?

Leonidas: szóstke masz źle zapisaną. Jedynka nie może być bo występuje tylko 1 raz. To samo dwójka. Wykorzystałaś już ją 2 razy w przypadku 1 i 2. Za to powinnaś dopisać tam 9, która może tam być użyta.

Leonidas: z resztą się zgadzam. Zapisałem to tak samo. Ale jednak wychodzi inaczej

małgosia: ups masz rację żle przepisałam z kartki ale mimo to jak sam zauważyłeś wychodzi inaczej 9*9*8*8*8*8 to dużo za dużo

małgosia: Czy ktoś mógłbym wskazać błąd w rozumowaniu? Byłabym wdzięczna

Rivi: Jak w pierwszej cyfrze masz 9 możliwości wg Ciebie, to jak nie wylosuje się "1" to już nigdzie jej nie będzie.. rozbijasz to na trzy opcje − kiedy 1 jest pierwsza, 2 jest pierwsza i inna jest pierwsza. Zobacz moje rozwiązanie z 18;14

małgosia: no dobrze ale mnożenie jest przemienne, równie dobrze ta cyfra z 1 jako opcją moze byc 2,3,4,5,6

Rivi: Tak, wszystko mam uwzględnione w swoich obliczeniach. jak zajmuje pierwsze miejsce, to dowolne z dwóch następnych zajmują "2" a trzy pozostałe jedne z 8 jak 2 jest pierwsza, to jedynka zajmuje jedno z 5, dwójka jedno z 4, a trzy pozostale jedne z 8 jak na poczatku jest cos innego niz 1 i 2, to 1 zajmuje jedno z 5 miejsc, 2 zajmują 2 z 4 pozostałych, a 2 pozostałe inne cyfry − z 8 cyfr... Nie można tego wszystkiego w jednym mnożeniu zmieścić jak Ty chcesz

małgosia: teraz niby rozumiem, ale trudno zastosować tę wiedzę w praktyce w każdym razie dziękuję

ewelinka: trudne to. normalnie mam ok 90 procent a tu ani 70 by nie było może. Mówię sobie ze właściwa będzie prosta

Jajko: Co powinno wyjść w 3−cim? Czyżby m∊R? Po zwinięciu wielomianu, wychodzi Δ=0 niezależnie od m − czy to ja sie gdzieś kopsnąłem?

aha: to, że Δ=0 nie oznacza, że nie ma miejsc zerowych, więc nie w tę stronę

Mordo: Zrobiłem, trochę okrężnym sposobem tę ilość liczb sześciocyfrowych... Wypisujemy: Ad.1) 1 na poczatku 122xxx, 1x22xx, 1xx22x, 1xxx22, 12x2xx, 1x2x2x, 1xx2x2, 12xx2x, 1x2xx2,12xxx2 −> 10 możliwości * 8³ (bo 8 cyfr możemy wstawić za każdego z x) Ad. 2) 2 na początku analogicznie: 212xxx, itd. z tym że tutaj 10 * 2 możliwości (*2, bo 12 lub 21) *8³ Ad. 3) x na początku (pierwszy x różny od 0) x122xx, x1x22x, x1xx22, x12x2x, x1x2x2, x12xx2 −> 6 możliwości * 7 (7 na cyfr może być na 1 miejscu "x") * 8² (8 cyfr może być na miejscu pozostałych dwóch "x") następnie x212xx itd. (analogicznie) i tu 6 możliwości * 2 (*2, bo 12 lub 21)* 7 * 8² Ad. 4) xx na poczatku xx122x, xx1x22, xx12x2 −> 3 możliwości * 7 * 8² (7 bo na miejscu pierwszego "x" 7 cyfr od 3 do 9, 8² bo na miejscu dwóch pozostałych "x" cyfry od 3 do 0) xx212x, itd. 3 * 2 (*2 bo 12 i 21 )* 7 * 8² Ad. 5) xxx na początku xxx122, xxx212, xxx221 −> 3 możliwości * 7 * 8² Zliczamy wszystko Ad. 1) 10*8³ = 5120 Ad. 2) 10*2*8³ = 10240 Ad. 3) 6*7*8² + (6*2)*7*8² = 8064 Ad. 4) 3*7*8² + (3*2)*7*8² = 4032 Ad. 5) 3*7*8² = 1344 Ad 1) + Ad 2) ... + Ad 5) = 28800

Mordo: Te x mogłem zamienić na xyz, ale myślę że będzie wiadomo o jaką koncepcję chodziło xd

Kaśka: A macie może zadanka z wyborczej ale na poziom podstawowy?

M4ciek: O super ktoś to wrzucił

Jajko: aha − doprowadziłem ten wielomian (zad 3) do postaci (x−2)(x⁴ − 2mx² + m²). Gdy za x² podstawimy t, to mamy równanie kwadratowe z Δ=0 − czyli jeden pierwiastek w równaniu z t (czyli dwa pierwiastki x=√t i x=−√t) oraz x₀ = 2. Są więc 3 pierwiastki, niezależnie od wartości m. Czy tak powinno to być?

Vax: Nie, wielomian zapisujemy w postaci: (x−2)(x²−m)² = (x−2)(x−√m)²(x+√m)² Jeden pierwiastek mamy już z pewnością, x=2, aby posiadał jeszcze tylko jeden pierwiastek musi zachodzić: x−2 = x−√m v x−2 = x+√m v x−√m = x+√m Z tego otrzymujemy, że dany wielomian ma 2 msc. zerowe jedynie dla m=0 v m=4 Pozdrawiam.

Jajko: mhm faktycznie (ja w ogóle źle zadanie przeczytałem i szukałem parametru dla trzech miejsc zerowych ) W zasadzie całkiem przyjemna ta matura − pare punktów by mi odjęli, ale ogółem chciałbym dostać podobną.

pedros: no może pazdro to to nie było, ale tak znowu bardzo łatwe to te zadania nie były myślę, że tak z 90% bym miał... Obstawiam też, że matura z CKE będzie prostsza...

Mordo: Jeśli nie będzie jakiegoś durnego zadania wymyślonego, tylko raczej schematyczne to damy radę Gorzej jak wymyślą jakieś zadanie, którego zdawalność będzie wynosiła mniej niż 1%

pedros: jak nie będą układać zadań od końca, jak Mr Pazdro to powinno być ok

Sza: Wróćmy jeszcze do 8 xD Nie rozumiem jak oni obliczyli to z tw. Pitagorasa. Mógłby mi ktoś to wytłumaczyć? i dlaczego c=1 ?

Rivi: c²=a²+b² dzielimy przez c²

	a2		a		b
1=		+{b2}{c2}=(		)2+(		)2
	c2		c		c

Daniel: mam pytanie do zadania 5. doszedłem do postaci 6sin²x + 2√3*sinxcosx=0. obie strony można podzielić przez 2 a następnie wyłączyć √3sin x przed nawias i powstaje postać: √3sinx (√3sinx + cos x)=0 √3 sinx=0 lub √3sinx+cosx=0 i teraz w tym drugim przypadeku przenoszę cos x na lewą stronę a następnie obie strony równania podnoszę do kwadratu i otrzymuję: 3sin²x=cos²x . korzystam z jedynki trygonometrycznej i powstaje: sin²x=¹₄ czyli sin x = ¹₂ lub sin x =− ¹₂. ostatecznie wychodzą mi rozwiązania x=0 lub x=−¹₆pi lub x= ¹₆ pi lub x= ⁵₆pi lub x = ⁷₆pi i to wszystko + 2kpi. rozwiązania wychodzą inne niż w odpowiedzi. czy ten sposób jest też poprawny?

johnan: mam pytanie do zadania 5

	√3
wychodzi w odpowiedzi tgx=−
	3

	5 π
potem x=		+ kπ
	6

	5 π		√3		π
Pytanie brzmi: Dlaczego		+ kπ , skoro dla tgx=−		, x jest −
	6		3		6

?

Godzio:

	5
Jak przesuniesz o jeden okres (dla k = 1) to otrzymasz		π + kπ
	6

Równie dobrze możesz odpowiedź zapisać w postaci:

	π		59π
x = −		+ kπ =		+ kπ −− to jest po prostu przesuwanie o okres
	6		6

tom215:

	√3
[P[johnan] poprostu jak narysujesz wykres funkcji tangens, i prostą y=		(jezeli sie
	3

	π		5π
nie myle) to punkt przecieciea sie z wykresem bedzie x = π −		+ kπ =		+ kπ
	6		6

johnan: racja ... straciłem ponad godzinę na tak banalną rozkminę... dzięki

Daniel: a mój sposób rozwiązania tego zadania ktoś skomentuje? dlaczego wychodzi inna odpowiedz?

Jack: zastanów się, czy podnosząc do kwadratu obie strony nie dodajesz przypadkiem rozwiązań (kwadrat zjada znaki)

johnan:

	1
skąd Ci się wzięzło sin2x=		?
	4

mi Twoim sposobem wychodzi 3sin²x−sin²x+1, następnie 2sin²x=−1

johnan: no i właśnie przy podnoszeniu do kwadratu z −cos²x powstał cos²x

Daniel: johnan według mnie wszystko zrobiłem poprawnie i zgodnie z zasadami matematycznymi. a sin²x=¹₄ ponieważ 3sin²x=1−sin²x więc jak przeniosę niewiadomą na lewą to powstanie tak jak napisałem

Maniek: Może ktoś pomóc z zadaniem 10 bo nie mam zielonego pojecia z której strony je ugryźć

Kosmos: moim zdaniem jeżeli ta prosta nie styka się z żadnym z tych punktów jest za mało informacji

Śmietana: Napisz sobie równanie okręgu: (x−a)²+(y−b)²=r² następnie za x i y podstaw współrzędne punktu A, a później B. Dodatkowo za a i b podstaw x i y z tej prostej przechodzącej przez środek. I tym oto magicznym sposobem masz dwa równania i dwie niewiadome. przyrównujesz oba równania do siebie bo po prawej stronie jest w obu r² no i wyliczasz współrzędne środka.Potem R jest odl. środka od punktu A lub B.

Rivi: Albo liczysz odległość AS oraz BS. Punkt S ma współrzędne (x, −x−3). Potem przyrównujesz AS=BS (bo są to promienie) i wyjdzie Ci współrzędna x. druga współrzędna −x−3 ; p promień − AS lub AB. I pozamiatane

Kosmos: kurde dobry jesteś śmietana

Śmietana: Powodzenia na maturze

Maniek: Nie dziękuję, bo jak nie pójdzie mi matma to z AGH mogę się pożegnać

Xengrin: Rivi. Wez daj jakis namiar. Masz piwo ode mnie. Dzieki tobie w koncu zrozumialem jak stosowac dwumian newtona, ktory w gruncie rzeczy jest prosty. Dzieki bardzo za wyjasnienie zadania z 6 cyfrowa liczba

ania21: Czy ktoś mógłby zrobić zad 11 ? Bo zaczynam liczyć a potem wychodzą takie liczby że sie odechciewa...

elpe: http://bi.gazeta.pl/im/0/9506/m9506530,MAT-ROZ.pdf dla tych ciekawskich którym coś nie wyszło