 Geometria na płaszczyźnie − rumpek
1.Trójkąty
a) Trójkąt równoboczny o boku a podzielono prostą l na dwie figury, których stosunek pól jest
równy 1 : 5. Prosta ta przecina bok AC w punkcie D pod kątem 15o, a bok AB w punkcie E.
Wykazać, że |AD| + |AE| = a
b) Punkt D leży na boku BC trójkąta równoramiennego ABC, w którym |AC| = |BC|. Odcinek AD
dzieli trójkąt ABC na dwa trójkąty równoramienne w taki sposób, że |AD| = |CD| oraz |AB| =
|BD|. Udowodnij, że |∡ADC| = 5 * |∡ACD|
c) Długości boków trójkąta ABC są kolejnymi wyrazami ciągu geometrycznego o ilorazie q. Wykaż
że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości
trójkąta ABC są równe miarom trójkąta ABC
d) Udowodnij, że trzy środkowe trójkąta dzielą go na 6 trójkątów o równych polach.
e) Udowodnij, że dwusieczne przecinają się w jednym punkcie
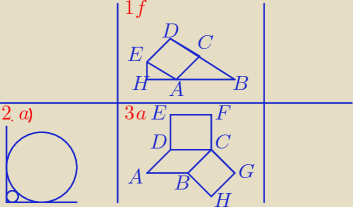
f) Na zewnątrz trójkąta prostokątnego ABC, w którym ∡ACB = 90° oraz AC = 5, BC = 12
zbudowano kwadrat ACDE. Punkt H leży na prostej AB i kąt ∡EHA = 90° .
Oblicz pole trójkąta HAE.
2.Okręgi
a) Dwa okręgi o środkach A i B są styczne zewnętrznie i każdy z nich jest jednocześnie styczny
do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów
do promienia mniejszego jest równy 3 + 2√2
b) Udowodnić, że w trójkącie prostokątnym suma przyprostokątnych jest
równa sumie średnic okręgu wpisanego i okręgu opisanego.
3.Czworokąty
a) Na bokach BC i CD równoległoboku ABCD zbudowano kwadraty CDEF i BCGH.
Udowodnij że |AC| = |FD|
b) Udowodnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
c) Wykaż, że prostokątem, którego obwód wynosi 2p, o największym polu jest kwadrat
Geometria na płaszczyźnie − rumpek
1.Trójkąty
a) Trójkąt równoboczny o boku a podzielono prostą l na dwie figury, których stosunek pól jest
równy 1 : 5. Prosta ta przecina bok AC w punkcie D pod kątem 15o, a bok AB w punkcie E.
Wykazać, że |AD| + |AE| = a
b) Punkt D leży na boku BC trójkąta równoramiennego ABC, w którym |AC| = |BC|. Odcinek AD
dzieli trójkąt ABC na dwa trójkąty równoramienne w taki sposób, że |AD| = |CD| oraz |AB| =
|BD|. Udowodnij, że |∡ADC| = 5 * |∡ACD|
c) Długości boków trójkąta ABC są kolejnymi wyrazami ciągu geometrycznego o ilorazie q. Wykaż
że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości
trójkąta ABC są równe miarom trójkąta ABC
d) Udowodnij, że trzy środkowe trójkąta dzielą go na 6 trójkątów o równych polach.
e) Udowodnij, że dwusieczne przecinają się w jednym punkcie
f) Na zewnątrz trójkąta prostokątnego ABC, w którym ∡ACB = 90° oraz AC = 5, BC = 12
zbudowano kwadrat ACDE. Punkt H leży na prostej AB i kąt ∡EHA = 90° .
Oblicz pole trójkąta HAE.
2.Okręgi
a) Dwa okręgi o środkach A i B są styczne zewnętrznie i każdy z nich jest jednocześnie styczny
do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów
do promienia mniejszego jest równy 3 + 2√2
b) Udowodnić, że w trójkącie prostokątnym suma przyprostokątnych jest
równa sumie średnic okręgu wpisanego i okręgu opisanego.
3.Czworokąty
a) Na bokach BC i CD równoległoboku ABCD zbudowano kwadraty CDEF i BCGH.
Udowodnij że |AC| = |FD|
b) Udowodnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
c) Wykaż, że prostokątem, którego obwód wynosi 2p, o największym polu jest kwadrat
| p | ||
o boku | ||
| 2 |
 Może porobię z ciekawości, ale nie będę tu wrzucać
Może porobię z ciekawości, ale nie będę tu wrzucać 

 dlatego może spróbuję, bo mam dość całek na dziś
dlatego może spróbuję, bo mam dość całek na dziś 

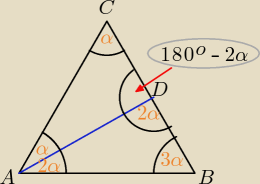 Zad 1
b)
Skoro |AC| i |BC| są bokami kąta równoramiennego to:
∡BAC = ∡ABC ⇔ α + 2α = 3α
∡ABC = 3α
∡BAC = 3α
Suma miar w trójkącie to 180o
α + α + 2α + 3α = 7α
7α = 180o
∡ADC = 180o − 2α ⇔ 7α − 2α = 5α
Więc prawdziwe jest ∡|ADC| = 5 * ∡|ACD|
Tak może być
Zad 1
b)
Skoro |AC| i |BC| są bokami kąta równoramiennego to:
∡BAC = ∡ABC ⇔ α + 2α = 3α
∡ABC = 3α
∡BAC = 3α
Suma miar w trójkącie to 180o
α + α + 2α + 3α = 7α
7α = 180o
∡ADC = 180o − 2α ⇔ 7α − 2α = 5α
Więc prawdziwe jest ∡|ADC| = 5 * ∡|ACD|
Tak może być  ?
?
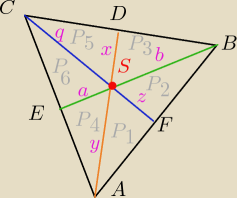 Dobra widzę, że Godziu na forum to robię dalej
Dobra widzę, że Godziu na forum to robię dalej  1 c) sobie póki co odpuszczę wrócę do niego jak zacznę ciągi
1 d)
Póki co do głowy przychodzi mi, że:
− środkowa dzieli trójkąt na dwa równe pola
− stosunek środkowych jest 2 : 1
Na podstawie drugiej myślnika:
1 c) sobie póki co odpuszczę wrócę do niego jak zacznę ciągi
1 d)
Póki co do głowy przychodzi mi, że:
− środkowa dzieli trójkąt na dwa równe pola
− stosunek środkowych jest 2 : 1
Na podstawie drugiej myślnika:
| y | 2 | ||
= | |||
| x | 1 |
| q | 2 | ||
= | |||
| z | 1 |
| b | 2 | ||
= | |||
| a | 1 |
| ah | ||
No i jak chyba dobrze myślę to można skorzystać ze wzoru: P = | ||
| 2 |
 może takie być czy co innego obmyślać
?
może takie być czy co innego obmyślać
? 
 Dobra na dobranoc zrobię sobie jeszcze jedno zadanko
Dobra na dobranoc zrobię sobie jeszcze jedno zadanko  4c
L = 2a + 2b
P = a*b
2p = 2a + 2b /: 2
p = a + b ⇒ a = p − b
P = (p − b) * b = −b2 + pb
Jest to funkcja kwadratowa z ramionami zwróconymi w dół, więc największą wartość ma w
wierzchołku.
4c
L = 2a + 2b
P = a*b
2p = 2a + 2b /: 2
p = a + b ⇒ a = p − b
P = (p − b) * b = −b2 + pb
Jest to funkcja kwadratowa z ramionami zwróconymi w dół, więc największą wartość ma w
wierzchołku.
| −p | p | |||
bw = | = | |||
| −2 | 2 |


 , nie można założyć, że x = a = z
Zad. 4
, nie można założyć, że x = a = z
Zad. 4
| p | p | |||
c) bw = | ⇒ a = | i teraz ok  | ||
| 2 | 2 |
 Jak jeszcze coś nie gra to mogę spróbować drugim sposobem który mam w głowie
Jak jeszcze coś nie gra to mogę spróbować drugim sposobem który mam w głowie 
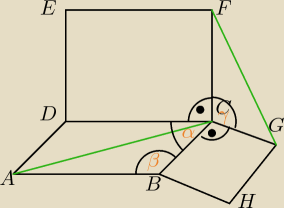 Zad 3
a)
Oczywiście CGBH jest kwadratem
Zad 3
a)
Oczywiście CGBH jest kwadratem  , trochę rysunek nie wyszedł
, trochę rysunek nie wyszedł Do zadanka: |AC| = |FG| więc wykaże na podstawie przystawiania
|AB| i |CD| jest równych długości ponieważ CDEF jest kwadratem, zatem boki:
|AB| = |CD| = |CF| = |ED| = |EF|
Kwadrat ma sumę kątów wewnętrznych 360o. Kąt ∡DCF ma miarę 90o (kwadrat CDEF)
oraz kąt ∡GCB ma również miarę 90o (kwadrat CBGH). Suma wszystkich kątów równoległoboku
wynosi 360o natomiast przy jednym boku suma dwóch kątów wynosi 180o. Rozpatrzmy zatem :
90o + γ + 90o + α = 360o
γ + α = 180o
W równoległoboku: α + β = 180o ⇔ α = 180o − β
Podstawiamy i otrzymujemy:
γ + 180o − β = 180o
γ = β
Boki |CB| i |AD| są równej długości ponieważ CGBH jest kwadratem więc:
|AD| = |BC| = |CG| = |BH| = |GH|
Zatem |AC| = |FG|
Do zadanka: |AC| = |FG| więc wykaże na podstawie przystawiania
|AB| i |CD| jest równych długości ponieważ CDEF jest kwadratem, zatem boki:
|AB| = |CD| = |CF| = |ED| = |EF|
Kwadrat ma sumę kątów wewnętrznych 360o. Kąt ∡DCF ma miarę 90o (kwadrat CDEF)
oraz kąt ∡GCB ma również miarę 90o (kwadrat CBGH). Suma wszystkich kątów równoległoboku
wynosi 360o natomiast przy jednym boku suma dwóch kątów wynosi 180o. Rozpatrzmy zatem :
90o + γ + 90o + α = 360o
γ + α = 180o
W równoległoboku: α + β = 180o ⇔ α = 180o − β
Podstawiamy i otrzymujemy:
γ + 180o − β = 180o
γ = β
Boki |CB| i |AD| są równej długości ponieważ CGBH jest kwadratem więc:
|AD| = |BC| = |CG| = |BH| = |GH|
Zatem |AC| = |FG| 
 )
)



 Zad 2 a)
1 rysunek ogólny zarys − ze środka wychodzą 2 promienie (a jak promienie to więc są równe)
tworzą więc kwadrat ABCD.
Teraz trochę objaśnień co do rysunku numer 2
Niebieska strzałka " r −> " oznacza promień od środka do punktu A
Środek (dolna czerwona strzałka) nazwałem punktem F
Punkt zetknięcia okręgów nazwałem punktem E (czerwona górna strzałka)
Skoro to jest kwadrat więc :
|AB| = |CB| = |CD| = |AD| = R
|CE| = R
Przekątna kwadratu (ABCD) wynosi R√2. Przekątna tego kwadratu składa się z odcinków:
|AC| = |AF| + |EF| + |EC|
R√2 = r + r√2 + R
Od razu napiszę skąd wziąłem r√2 − dokładnie tak samo jak z kwadratem ABCD. Na rysunku numer
2 widać różowe małe boki − są to boki kwadratu. A odcinek |AF| jest przekątną więc r√2
Na tym rysunku numer 2 nie można dostrzec ale tam jest jeszcze taka niewielka odległość którą
specjalnie zaznaczyłem na rysunku numer 1 (zielona strzałka)(u siebie na kartce mam znacznie
wyraźniej
Zad 2 a)
1 rysunek ogólny zarys − ze środka wychodzą 2 promienie (a jak promienie to więc są równe)
tworzą więc kwadrat ABCD.
Teraz trochę objaśnień co do rysunku numer 2
Niebieska strzałka " r −> " oznacza promień od środka do punktu A
Środek (dolna czerwona strzałka) nazwałem punktem F
Punkt zetknięcia okręgów nazwałem punktem E (czerwona górna strzałka)
Skoro to jest kwadrat więc :
|AB| = |CB| = |CD| = |AD| = R
|CE| = R
Przekątna kwadratu (ABCD) wynosi R√2. Przekątna tego kwadratu składa się z odcinków:
|AC| = |AF| + |EF| + |EC|
R√2 = r + r√2 + R
Od razu napiszę skąd wziąłem r√2 − dokładnie tak samo jak z kwadratem ABCD. Na rysunku numer
2 widać różowe małe boki − są to boki kwadratu. A odcinek |AF| jest przekątną więc r√2
Na tym rysunku numer 2 nie można dostrzec ale tam jest jeszcze taka niewielka odległość którą
specjalnie zaznaczyłem na rysunku numer 1 (zielona strzałka)(u siebie na kartce mam znacznie
wyraźniej  )
Dobra jedziemy dalej:
jak mamy już:
R√2 = r + r√2 + R
To pozostaje tylko:
R√2 − R = r√2 + r
R(√2 − 1) = r(√2 + 1)
Moim zadaniem jest udowodnić, że stosunek promienia R do r wynosi 3 + 2√2 więc
dzielę przez r:
R(√2 − 1) = r(√2 + 1) / :r
)
Dobra jedziemy dalej:
jak mamy już:
R√2 = r + r√2 + R
To pozostaje tylko:
R√2 − R = r√2 + r
R(√2 − 1) = r(√2 + 1)
Moim zadaniem jest udowodnić, że stosunek promienia R do r wynosi 3 + 2√2 więc
dzielę przez r:
R(√2 − 1) = r(√2 + 1) / :r
| R(√2 − 1) | |
= √2 + 1 / : (√2 − 1) | |
| r |
| R | √2 + 1 | ||
= | |||
| r | √2 − 1 |
| R | √2 + 1 | √2 + 1 | |||
= | * | ||||
| r | √2 − 1 | √2 + 1 |
| R | (√2 + 1)2 | ||
= | |||
| r | 2 − 1 |
| R | 2 + 2√2 + 1 | ||
= | |||
| r | 1 |
| R | |
= 3 + 2√2 | |
| r |
 Tymczasem muszę uciekać i będę koło 23, na pewno jakieś zadanko jeszcze ruszę
Tymczasem muszę uciekać i będę koło 23, na pewno jakieś zadanko jeszcze ruszę 

 Dobra czas wziąć się za resztę zadań
Dobra czas wziąć się za resztę zadań  Zacznijmy pierwsze
Zacznijmy pierwsze  (głęboka woda)
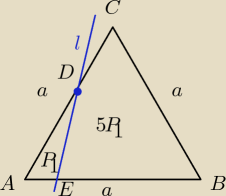
a) Trójkąt równoboczny o boku a podzielono prostą l na dwie figury, których stosunek pól jest
równy 1 : 5. Prosta ta przecina bok AC w punkcie D pod kątem 15o, a bok AB w punkcie E.
Wykazać, że |AD| + |AE| = a
Taki rysunek może być ?
(głęboka woda)
a) Trójkąt równoboczny o boku a podzielono prostą l na dwie figury, których stosunek pól jest
równy 1 : 5. Prosta ta przecina bok AC w punkcie D pod kątem 15o, a bok AB w punkcie E.
Wykazać, że |AD| + |AE| = a
Taki rysunek może być ?

 Szybko przeleciało mi przez myśl coś z podobieństwa figur ale wywaliłem tę myśl
Szybko przeleciało mi przez myśl coś z podobieństwa figur ale wywaliłem tę myśl  Jakaś wskazówka
Jakaś wskazówka  ?
?
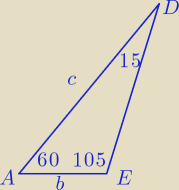 Wyraź b i c poprzez a, (pole i tw. sinusów). To jest wskazówka
Wyraź b i c poprzez a, (pole i tw. sinusów). To jest wskazówka
 bo tego nie miałem
bo tego nie miałem

 180o = 60o + 15o + α
180o − 60o − 15o = α
α = 115o
Stąd
180o = 60o + 15o + α
180o − 60o − 15o = α
α = 115o
Stąd  Godziu mam prośbę do Ciebie − mógłbyś jakieś znaleźć zadania z zastosowaniem twierdzenia
sinusów
Godziu mam prośbę do Ciebie − mógłbyś jakieś znaleźć zadania z zastosowaniem twierdzenia
sinusów  ? Chciałbym sobie je przećwiczyć zanim zacznę robić to zadanie
? Chciałbym sobie je przećwiczyć zanim zacznę robić to zadanie
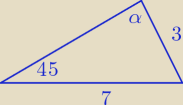 Dany jest trójkąt o bokach 3 i 7 i kącie 45o(jak na rys.) oblicz sinus kąta α, takie zadanie
na szybko wymyślone
Dany jest trójkąt o bokach 3 i 7 i kącie 45o(jak na rys.) oblicz sinus kąta α, takie zadanie
na szybko wymyślone 
| 3 | 7 | ||
= | |||
| sin45o | sinα |
| 3 | 7 | ||||||||
= | |||||||||
| sinα |
| 7√2 | ||
3sinα = | / :3 | |
| 2 |
| 7√2 | ||
sinα = | ||
| 6 |

 wiece jakbys Godzio znalazł jakieś fajne zadania
jeszcze z Twierdzenia Sinusów to bardzo chętnie zerknę
wiece jakbys Godzio znalazł jakieś fajne zadania
jeszcze z Twierdzenia Sinusów to bardzo chętnie zerknę 
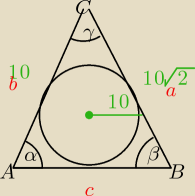 Godzio znalazłem chyba jakieś zadanie z zastosowaniem twierdzenia sinusów
Godzio znalazłem chyba jakieś zadanie z zastosowaniem twierdzenia sinusów  mógłbyś
sprawdzić czy dobrze ? Jakbyś miał podobne to chętnie zobaczę
mógłbyś
sprawdzić czy dobrze ? Jakbyś miał podobne to chętnie zobaczę  W trójkącie ABC są dane: AC = 10, BC = 10√2. Promień okręgu opisanego na tym trójkącie:
R = 10. Oblicz miarę kąta ACB.
Rysunek przykładowy na górze
Twierdzenie sinusów:
W trójkącie ABC są dane: AC = 10, BC = 10√2. Promień okręgu opisanego na tym trójkącie:
R = 10. Oblicz miarę kąta ACB.
Rysunek przykładowy na górze
Twierdzenie sinusów:
| a | b | c | |||
= | = | = 2R | |||
| sinα | sinβ | sinγ |
| 10√2 | |
= 2 * 10 | |
| sinα |
| 10√2 | |
= 20 / *sinα | |
| sinα |
| √2 | ||
sinα = | (α = 45o) | |
| 2 |
| 10 | |
= 2 * 10 | |
| sinβ |
| 10 | |
= 20 / * sinβ | |
| sinβ |
| 1 | ||
sinβ = | (β = 30o) | |
| 2 |
 ?
?

 To mam kolejne zadanie:
W trójkącie ABC mamy dane: |AC| = √3 i |∡ACB| = 90o. Przez wierzchołek C poprowadzono
prostą, która utworzyła z bokiem AC kąt 60o i przecięła bok AB w punkcie D tak,
że |AD| : |DB| = 1 : 3.
a) Wykonaj rysunek
b) Oblicz długość boków AB i BC oraz długość odcinka CD
a) Rysunek wyżej, dobrze ?
To mam kolejne zadanie:
W trójkącie ABC mamy dane: |AC| = √3 i |∡ACB| = 90o. Przez wierzchołek C poprowadzono
prostą, która utworzyła z bokiem AC kąt 60o i przecięła bok AB w punkcie D tak,
że |AD| : |DB| = 1 : 3.
a) Wykonaj rysunek
b) Oblicz długość boków AB i BC oraz długość odcinka CD
a) Rysunek wyżej, dobrze ?


 robię dalej
robię dalej 


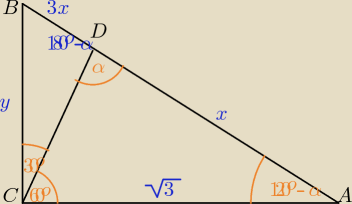 Ok, to robię dalej
Ok, to robię dalej  |AB|2 = |AC|2 + |BC|2
16x2 = 3 + y2
y2 = 16x2 − 3
y = √16x2 − 3
W trójkącie ACD twierdzenie sinusów:
|AB|2 = |AC|2 + |BC|2
16x2 = 3 + y2
y2 = 16x2 − 3
y = √16x2 − 3
W trójkącie ACD twierdzenie sinusów:
| √3 | x | ||
= | |||
| sinα | sin60o |
| √3 | x | ||||||||
= | |||||||||
| sinα |
|
| √3 | ||
sinα * x = | * √3 | |
| 2 |
| 3 | ||
sinα = | ||
| 2x |
| y | 3x | ||
= | |||
| 180o − α | sin30o |
| √16x2 − 3 | 3x | ||||||||
= | |||||||||
| sinα |
|
| √16x2 − 3 | 3x | |||||||||||||||||
= | ||||||||||||||||||
|
|
| 3 | 1 | |||
3x * | = √16x2 − 3 * | |||
| 2x | 2 |
| 9 | √16x2 − 3 | ||
= | / *2 | ||
| 2 | 2 |
| 21 | ||
x2 = | ||
| 4 |
| √21 | √21 | |||
x = | v x = − | ∉ N | ||
| 2 | 2 |
| 21 | ||
y = √16 * | − 3 | |
| 4 |
| √21 | ||
|AB| = 4 * | = 2√21 | |
| 2 |

| y | 3x | y | |||
= | ⇒ | = xsinα | |||
| sinα | sin30 | 6 |
| x | √3 | 3 | |||
= | ⇒ xsinα = | ||||
| sin60 | sinα | 2 |
| y | 3 | ||
= | |||
| 6 | 2 |
| 84 | ||
x2 = | ||
| 16 |
| 2√21 | √21 | |||
x = | = | |||
| 4 | 2 |
 Co mnie cieszy
Co mnie cieszy



 )
)
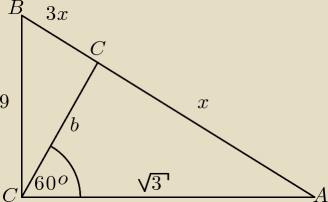 Ok, jeszcze raz rysunek wyżej
Ok, jeszcze raz rysunek wyżej  x2 = (√3)2 + b2 − 2 * (√3) * b * cos60o
x2 = (√3)2 + b2 − 2 * (√3) * b * cos60o
| 1 | ||
(U{√21{2})2 = 3 + b2 − 2√3 * b * | ||
| 2 |
| 21 | |
= 3+ b2 − √3b / * 4 | |
| 4 |
| 4√3 − 8√3 | ||
b1 = | = U{−4√3{8} ∉ N | |
| 8 |
| 4√3 + 8√3 | 12√3 | 3√3 | ||||
b2 = | = | = | ||||
| 8 | 8 | 2 |
| 3√3 | ||
|CD| = | ||
| 2 |
| √21 | 1 | |||
( | )2 = 3 + b2 − 2√3 * b * | |||
| 2 | 2 |
| 4√3 − 8√3 | −4√3 | |||
b1 = | = | ∉ N | ||
| 8 | 8 |
 ?
?
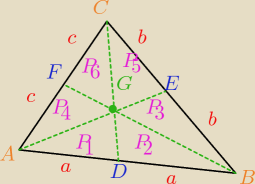 Robię kolejne podejście do:
"Udowodnij, że trzy środkowe trójkąta dzielą go na 6 trójkątów o równych polach."
Robię kolejne podejście do:
"Udowodnij, że trzy środkowe trójkąta dzielą go na 6 trójkątów o równych polach."  Rysunek powyżej.
Najpierw krótko o środkowych trójkąta:
− przecinają się w jednym punkcie
− jedna środkowa dzieli trójkąt na dwa trójkąty o równych polach
1o Odcinek |CD| jest środkową w trójkąta ABC, czyli na podstawie tego co wyżej napisałem:
PADC = PCDB, zatem: Pole PADC składa się z c + c+ a, natomiast pole PCDB z:
b + b + a.
Przyrównując to ze sobą: c + c + a = b + b + a ⇔ 2c + a = 2b + a ⇒ 2c = 2b : 2 ⇒ c = b
2o Odcinek |AE| jest środkową w trójkąta ABC, czyli znowu:
PAEC = PAEB, zatem: Pole PAEC składa się z c + c+ b, natomiast pole PAEB z:
b + a + a.
Przyrównując to ze sobą: c + c + b = b + a + a ⇔ 2c + b = 2a + b ⇒ 2c = 2a : 2 ⇒ c = a
3o Odcinek |BF| jest środkową w trójkąta ABC, czyli:
PBFA = PBFC, zatem: Pole PBFA składa się z a + a + c, natomiast pole PBFC z:
b + b + c.
Przyrównując to ze sobą: a + a + c = b + b + c ⇔ 2a + c = 2b + c ⇒ 2a = 2b : 2 ⇒ a = b
Zatem mają równe pola ponieważ mają odpowiednie części (połowy) równe. c.n.u
Tyle wystarczy czy coś dopisać? Czy może coś zmienić
Rysunek powyżej.
Najpierw krótko o środkowych trójkąta:
− przecinają się w jednym punkcie
− jedna środkowa dzieli trójkąt na dwa trójkąty o równych polach
1o Odcinek |CD| jest środkową w trójkąta ABC, czyli na podstawie tego co wyżej napisałem:
PADC = PCDB, zatem: Pole PADC składa się z c + c+ a, natomiast pole PCDB z:
b + b + a.
Przyrównując to ze sobą: c + c + a = b + b + a ⇔ 2c + a = 2b + a ⇒ 2c = 2b : 2 ⇒ c = b
2o Odcinek |AE| jest środkową w trójkąta ABC, czyli znowu:
PAEC = PAEB, zatem: Pole PAEC składa się z c + c+ b, natomiast pole PAEB z:
b + a + a.
Przyrównując to ze sobą: c + c + b = b + a + a ⇔ 2c + b = 2a + b ⇒ 2c = 2a : 2 ⇒ c = a
3o Odcinek |BF| jest środkową w trójkąta ABC, czyli:
PBFA = PBFC, zatem: Pole PBFA składa się z a + a + c, natomiast pole PBFC z:
b + b + c.
Przyrównując to ze sobą: a + a + c = b + b + c ⇔ 2a + c = 2b + c ⇒ 2a = 2b : 2 ⇒ a = b
Zatem mają równe pola ponieważ mają odpowiednie części (połowy) równe. c.n.u
Tyle wystarczy czy coś dopisać? Czy może coś zmienić  ?
?
 ?
?



 "Wykaż" to najgorsze co może być
"Wykaż" to najgorsze co może być  Ale mam kolejne zadanie zrobione
Ale mam kolejne zadanie zrobione  Z trójkątów to ostatnie
Z trójkątów to ostatnie  (trzeba było raczej z podobieństwa skorzystać
(trzeba było raczej z podobieństwa skorzystać  ) Zaraz wrzucę
) Zaraz wrzucę
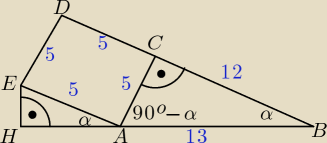 Zadanie 1 f)
"Na zewnątrz trójkąta prostokątnego ABC, w którym ∡ACB = 90° oraz AC = 5, BC = 12 zbudowano
kwadrat ACDE. Punkt H leży na prostej AB i kąt ∡EHA = 90° . Oblicz pole trójkąta HAE. "
Rysunek powyżej
(trochę taki prostokąt wyszedł ale nic nie szkodzi chyba bo to tylko przykładowy rysunek
Zadanie 1 f)
"Na zewnątrz trójkąta prostokątnego ABC, w którym ∡ACB = 90° oraz AC = 5, BC = 12 zbudowano
kwadrat ACDE. Punkt H leży na prostej AB i kąt ∡EHA = 90° . Oblicz pole trójkąta HAE. "
Rysunek powyżej
(trochę taki prostokąt wyszedł ale nic nie szkodzi chyba bo to tylko przykładowy rysunek  )
Skoro bok |AC| ma długość 5 to boki kwadratu ACDE też będą tyle miały, oraz przekątna
mniejszego trójkąta będzie miała 5 (|AE|). W tym większym trójkącie oznaczyłem już kąty. Skąd
się wzięło 90o − α , chyba wiadomo
)
Skoro bok |AC| ma długość 5 to boki kwadratu ACDE też będą tyle miały, oraz przekątna
mniejszego trójkąta będzie miała 5 (|AE|). W tym większym trójkącie oznaczyłem już kąty. Skąd
się wzięło 90o − α , chyba wiadomo  (180 − 90o (bo trójkąt prostokątny) − α ⇔ 90o − α )
I ten mniejszy trójkąt jest podobny do tego większego mający kąt prosty ∡AHE (zaznaczyłem).
Możemy wyliczyć przeciwprostokątną |AB| większego trójkąta:
|AB|2 = |AC|2 + |CB|2
|AB|2 = 52 + 122
|AB|2 = 25 + 144
|AB|2 = 169
|AB| = 13
(180 − 90o (bo trójkąt prostokątny) − α ⇔ 90o − α )
I ten mniejszy trójkąt jest podobny do tego większego mający kąt prosty ∡AHE (zaznaczyłem).
Możemy wyliczyć przeciwprostokątną |AB| większego trójkąta:
|AB|2 = |AC|2 + |CB|2
|AB|2 = 52 + 122
|AB|2 = 25 + 144
|AB|2 = 169
|AB| = 13
| 1 | ||
PABC = | * a * h | |
| 2 |
| 1 | ||
PABC = | * 5 * 12 | |
| 2 |
| 5 | ||
zatem skala podobieństwa wynosi: k = | ||
| 13 |
| 25 | ||
k2 = | ||
| 169 |
| 25 | ||
PAEH = | * 30[j2] | |
| 169 |
| 750 | ||
PAEH = | [j2] | |
| 169 |



 3 b)
Rysunek powyżej
3 b)
Rysunek powyżej  Środkiem odcinka |AB| jest punkt E
Środkiem odcinka |BC| jest punkt F
Środkiem odcinka |CD| jest punkt G
Środkiem odcinka |AD| jest punkt H
Z twierdzenia Talesa mamy:
Środkiem odcinka |AB| jest punkt E
Środkiem odcinka |BC| jest punkt F
Środkiem odcinka |CD| jest punkt G
Środkiem odcinka |AD| jest punkt H
Z twierdzenia Talesa mamy:
| |HD| | |AD| | ||
= | |||
| |DG| | |DC| |
| |DH| | |DA| | |DH| | 2|DH| | ||||
= | ⇔ | = | ⇒ |DH|*|AC| = 2|DH| * |HG| | ||||
| |HG| | |AC| | |HG| | |AC| |
| |BF| | |BC| | ||
= | |||
| |BE| | |BA| |
 otrzymujemy:
otrzymujemy:
| |BF| | |BC| | |BF| | 2|BF| | ||||
= | ⇔ | = | ⇒ |BF|*|AC| = 2|BF| * |EF| | ||||
| |EF| | |AC| | |EF| | |AC| |
 ?
?
 Tymczasem idę oglądać film
Tymczasem idę oglądać film 


 Dobra czas znowu spróbować:
"Udowodnij, że trzy środkowe trójkąta dzielą go na 6 trójkątów o równych polach. "
Najpierw jednak spróbuje zrobić prostsze czyli:
"Udowodnij, że środkowa trójkąta dzieli go na 2 trójkąty o równych polach"
Rysunek powyżej
No to teraz wykazanie:
Dobra czas znowu spróbować:
"Udowodnij, że trzy środkowe trójkąta dzielą go na 6 trójkątów o równych polach. "
Najpierw jednak spróbuje zrobić prostsze czyli:
"Udowodnij, że środkowa trójkąta dzieli go na 2 trójkąty o równych polach"
Rysunek powyżej
No to teraz wykazanie:
| 1 | ah | |||
PADC = | * a * h = | |||
| 2 | 2 |
| 1 | ah | |||
PDBC = | * a * h = | |||
| 2 | 2 |
 Muszę od czegoś zacząć
Muszę od czegoś zacząć 

 Szocke
Szocke 
| x | 1 | |||
Pisałeś żeby wykorzystać ten stosunek: | = | to przychodzi mi do głowy tylko to aby | ||
| y | 2 |
 Zaraz zrobię
Zaraz zrobię  Chyba już wiem o co chodzi
Chyba już wiem o co chodzi 
| 1 | ||
P = | absinα, Myślę, że zaraz dojdziesz do rozwiązania  | |
| 2 |
| 1 | ||
Racja literówka  zapomniałem o zapomniałem o | ||
| 2 |
 Sorki musiałem na chwile wyjść, już piszę:
Rysunek wyżej.
Na podstawie tym że "Środek ciężkości dzieli każdą środkową w stosunku 2 : 1" otrzymujemy:
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
* środkowa |CD|:
Sorki musiałem na chwile wyjść, już piszę:
Rysunek wyżej.
Na podstawie tym że "Środek ciężkości dzieli każdą środkową w stosunku 2 : 1" otrzymujemy:
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
* środkowa |CD|:
| |CG| | 2 | |||
= | ||||
| |DG| | 1 |
| |AG| | 2 | |||
= | ||||
| |EG| | 1 |
| |BG| | 2 | |||
= | ||||
| |FG| | 1 |
 nie pamiętam jak to się nazywało
nie pamiętam jak to się nazywało  )
No to teraz tak jak wyżej, kombinujemy z polem tylko teraz ze wzorem:
)
No to teraz tak jak wyżej, kombinujemy z polem tylko teraz ze wzorem:
| 1 | ||
P = | * a * b * sinα. | |
| 2 |
| 1 | 2zysinα | |||
P3 = | *2z*y*sinα = | = zysinα | ||
| 2 | 2 |
| 1 | 2yzsinα | |||
P4 = | *2y*z*sinα = | = zysinα | ||
| 2 | 2 |
| 1 | 2yxsinβ | |||
P2 = | *2y*x*sinβ = | = xysinβ | ||
| 2 | 2 |
| 1 | 2xysinβ | |||
P5 = | *2x*y*sinβ = | = xysinβ | ||
| 2 | 2 |
| 1 | 2zxsinγ | |||
P1 = | *2z*x*sinγ = | = xzsinγ | ||
| 2 | 2 |
| 1 | 2xzsinγ | |||
P6 = | *2x*z*sinγ = | = xzsinγ | ||
| 2 | 2 |
 )
Zatem prawdziwe jest P1 = P2 = P3 = P4 = P5 = P6
c.n.u.
Tak może być Godziu?
)
Zatem prawdziwe jest P1 = P2 = P3 = P4 = P5 = P6
c.n.u.
Tak może być Godziu?  To rysowanie trójkątów z środkowymi jest trochę męczące
To rysowanie trójkątów z środkowymi jest trochę męczące 



 odale Ci 100zl od godziny
odale Ci 100zl od godziny

 Zwłaszcza jak mi dadzą jakąś rzeźnie z prawdopodobieństwa
Zwłaszcza jak mi dadzą jakąś rzeźnie z prawdopodobieństwa
 To 10 zadań zrobisz w nie całą godzinkę, a na prawdopodobieństwo
będziesz miał 2h
To 10 zadań zrobisz w nie całą godzinkę, a na prawdopodobieństwo
będziesz miał 2h  więc 100% luźno będzie, poza tym zasługujesz na te 100%
więc 100% luźno będzie, poza tym zasługujesz na te 100% 

 Zanim zacznę to główne zadanko z dwusieczną to na razie takie moje wprowadzające:
"Wykaż, że dwusieczne dwóch sąsiednich kątów w równoległoboku są do siebie prostopadłe."
Nawet to zadanko proste. Znowu korzystam z tego że suma kątów przy jednym ramieniu wynosi 180o
(bodajże korzystałem z niech przy 3a)
2α + 2β = 180o
α + β = 90o
No i teraz rozpatrujemy trójkąt: ABE: 180o − (α − β) = 90o
c.n.u.
No i teraz moje pytanie: skoro są do siebie prostopadłe to właśnie tutaj się przecinają
teoretycznie
Zanim zacznę to główne zadanko z dwusieczną to na razie takie moje wprowadzające:
"Wykaż, że dwusieczne dwóch sąsiednich kątów w równoległoboku są do siebie prostopadłe."
Nawet to zadanko proste. Znowu korzystam z tego że suma kątów przy jednym ramieniu wynosi 180o
(bodajże korzystałem z niech przy 3a)
2α + 2β = 180o
α + β = 90o
No i teraz rozpatrujemy trójkąt: ABE: 180o − (α − β) = 90o
c.n.u.
No i teraz moje pytanie: skoro są do siebie prostopadłe to właśnie tutaj się przecinają
teoretycznie 
 To musi być romb
To musi być romb
 Tylko nie dopisałem do polecenia, chodziło mi o trzy dwusieczne w trójkącie
Tylko nie dopisałem do polecenia, chodziło mi o trzy dwusieczne w trójkącie



 jakie miało być
jakie miało być  ?
I takie pytanie: "Udowodnij, że dwusieczne przecinają się w jednym punkcie " do tego polecenia
może być taki dowód jaki przeprowadziłem w górnym dowodzie
?
I takie pytanie: "Udowodnij, że dwusieczne przecinają się w jednym punkcie " do tego polecenia
może być taki dowód jaki przeprowadziłem w górnym dowodzie  ?
?

 Taki rysunek może być?
Taki rysunek może być?


 Ale to Ci raczej nic nie da
Ale to Ci raczej nic nie da
 ?
?

 ?
?

 ?
?


 I wychodzi na to że zostanie jedno zadanie z okręgiem do zrobienia i to
najgorsze pierwsze
I wychodzi na to że zostanie jedno zadanie z okręgiem do zrobienia i to
najgorsze pierwsze  (Do tego z ciągiem tak jak pisałem wrócę − jak będę miał ciągi jeszcze w
tym roku to przed wakacjami, a jak nie bede mial ciagów w tym roku szkolnym to będę miał co
robić przez wakację
(Do tego z ciągiem tak jak pisałem wrócę − jak będę miał ciągi jeszcze w
tym roku to przed wakacjami, a jak nie bede mial ciagów w tym roku szkolnym to będę miał co
robić przez wakację .Ogólnie wakacje mam już zarezerwowane dla ćwiczenia z matematyki
.Ogólnie wakacje mam już zarezerwowane dla ćwiczenia z matematyki  i
robieniu ciekawych zadań )
i
robieniu ciekawych zadań )
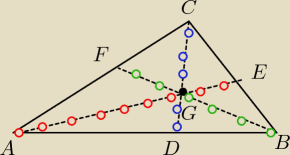 Rysunek taki jak przedtem
Rysunek taki jak przedtem  Dwusieczna dzieli kąt na 2 równe kąty
1o
Rozpatrzmy najpierw to że każdy punkt obrany na dwusiecznej |CD| jest w równych odległościach
od odcinków |AC| oraz |CB|. (Niebieskie otwarte kropeczki)
2o
Teraz rozpatrzmy drugą dwusieczną |AE| również każdy punkt obrany na tej dwusiecznej jest w
równych odległościach od |AB| oraz |AC|. (Czerwone otwarte kropeczki)
3o
Teraz pozostała nam tylko ostatnia dwusieczna: |BF|. Każdy punkt obrany na tej dwusiecznej jest
w równych odległościach od |BC| oraz |AB| (zielone otwarte kropeczki)
Więc na pewno dwusieczne trójkąta przetną się w jednym punkcie.
c.n.u.
Godziu tyle starczy, czy coś dopisać
Dwusieczna dzieli kąt na 2 równe kąty
1o
Rozpatrzmy najpierw to że każdy punkt obrany na dwusiecznej |CD| jest w równych odległościach
od odcinków |AC| oraz |CB|. (Niebieskie otwarte kropeczki)
2o
Teraz rozpatrzmy drugą dwusieczną |AE| również każdy punkt obrany na tej dwusiecznej jest w
równych odległościach od |AB| oraz |AC|. (Czerwone otwarte kropeczki)
3o
Teraz pozostała nam tylko ostatnia dwusieczna: |BF|. Każdy punkt obrany na tej dwusiecznej jest
w równych odległościach od |BC| oraz |AB| (zielone otwarte kropeczki)
Więc na pewno dwusieczne trójkąta przetną się w jednym punkcie.
c.n.u.
Godziu tyle starczy, czy coś dopisać  ?
?



 Cóż, że po miesiącu − liczą się chęci
Cóż, że po miesiącu − liczą się chęci  "Udowodnić, że w trójkącie prostokątnym suma przyprostokątnych jest równa sumie średnic okręgu
wpisanego i okręgu opisanego. "
1. Promień okręgu wpisanego w trójkąt:
"Udowodnić, że w trójkącie prostokątnym suma przyprostokątnych jest równa sumie średnic okręgu
wpisanego i okręgu opisanego. "
1. Promień okręgu wpisanego w trójkąt:
| 2P | ||
r = | ||
| a + b + c |
| 1 | ||
P = | ab | |
| 2 |
| c | ||
r = | , gdzie c jest przeciwprostokątną trójkąta prostokątnego | |
| 2 |
| 2ab | c2 + ca + cb + 2ab | |||
2r + 2r1 = c + | = | = | ||
| a + b + c | a + b + c |
| a2 + 2ab + b2 + ac + bc | (a + b)2 + c(a + b) | |||
= | = | = | ||
| a + b + c | a + b + c |
| (a + b)(a + b + c) | ||
= | = a + b | |
| a + b + c |
 Najtrudniejsze
Najtrudniejsze




| 1 | ||
R = | c | |
| 2 |
| a + b − c | ||
r = | ||
| 2 |

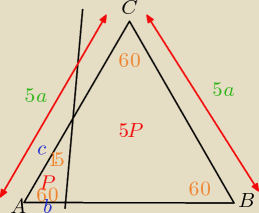 Napisałeś we wskazówce, żeby skorzystać twierdzenia sinusów i wyrazić b i c poprzez a
Czyli w tym wypadku 5a
Napisałeś we wskazówce, żeby skorzystać twierdzenia sinusów i wyrazić b i c poprzez a
Czyli w tym wypadku 5a  ?
?
| √3 | ||
P = | cb | |
| 2 |

| sin105o | sin15o | ||
= | |||
| c | b |
| √6 − √2 | ||
sin15o = sin(45o − 30o) = | ||
| 2 |
| √2 + √6 | ||
= | ||
| 4 |
| c | b | ||
= | |||
| sin115o | sin15o |
| c | b | ||||||||||||||
= | |||||||||||||||
|
|
| c(√2 − √6) | b(√2 + √6) | ||
= | / * 4 | ||
| 4 | 4 |
| √2 + √6 | √2 + √6 | |||
c = b * | * | |||
| √2 − √6 | √2 + √6 |
| (√2 + √6)2 | ||
c = b * | ||
| 2 − 6 |
| 2 + 2√12 + 6 | ||
c = b * | ||
| −4 |
 ?
?
| √6 − √2 | √2 − √6 | |||
sin16 = | , a nie |  | ||
| 4 | 4 |


| c(√6 − √2) | b(√2 + √6) | ||
= | / * 4 | ||
| 4 | 4 |
| √2 + √6 | √6 + √2 | |||
c = b * | * | |||
| √6 − √2 | √6 + √2 |
| (√2 + √6)2 | ||
c = b * | ||
| 6 − 2 |
| 2 + 2√12 + 6 | ||
c = b * | ||
| 4 |
| 2b(4 + √12 | ||
c = | ||
| 4 |
| b(4 + 2√3) | ||
c = | ||
| 2 |
 ?
Skąd masz takie fajne zadanko
?
Skąd masz takie fajne zadanko  ?
?

| √3 | ||
P = | cb | |
| 2 |
| √3 | |
* (2b + √3b) | |
| 2 |


 ?
?
 I prośba: mógłbyś znowu coś uszykować
I prośba: mógłbyś znowu coś uszykować  ?
?
| a2√3 | ||
6P = | ⇒ P = ... | |
| 4 |
| 1 | ||
P = | bcsin60o | |
| 2 |
 ? Czy nie potrzebne przy tym zadaniu?
? Czy nie potrzebne przy tym zadaniu?
