geometria analityczna crazy nati: Znajdź współrzędne środka okręgu opisanego na trójkącie o wierzchołkach: A=(6,1) B=(−2,5) C=(−6,−1)

Gustlik: Podstawiasz współrzędne tych trzech punktów do równania okregu: (x−a)²+(y−b)²=r² Otrzymasz układ równań: {(6−a)²+(1−b)²=r² (1) {(−2−a)²+(5−b)²=r² (2) {(−6−a)²+(−1−b)²=r² (3) {36−12a+a²+1−2b+b²=r² (1) {4+4a+a²+25−10b+b²=r² (2) {36+12a+a²+1+2b+b²=r² (3) Odejmij stronami (1)−(2) i (1)−(3) − otrzymasz dwa równania liniowe: {32−16a−24+8b=0 {−24a−4b=0 {8−16a+8b=0 {−24a−4b=0 {−16a+8b=−8 /:8 {−24a−4b=0 /:4 {−2a+b=−1 {−6a−b=0 + −−−−−−−−−−−−−−−−−−−−−− −8a=−1 /:(−8)

	1
a=
	8

	1
−2*		+b=−1
	8

	1
−		+b=−1
	4

	1
b=−1+
	4

	3
b=−
	4

II sposób: Można też zastosować równanie ogólne − wtedy nie będziesz miała kwadratów: x²+y²+Ax+By+C=0 {36+1+6A+B+C=0 {4+25−2A+5B+C=0 {36+1−6A−B+C=0 {6A+B+C=−37 (1) {−2A+5B+C=−29 (2) {−6A−B+C=−37 (3) Odejmę stronami (1) i (2) oraz (1) i (3): {8A−4B=−8 /:4 {12A+2B=0 /:2 {2A−B=−2 {6A+B=0 + −−−−−−−−−−−−−−−−−−−−−−− 8A=−2 /:8

	−2		1
A=		=−
	8		4

B=−6A

	1		6		3
B=−6*(−		)=		=
	4		4		2

Podstawiam A i B do (1)

	1		3
{6*(−		)+		+C=−37
	4		2

	3		3
−		+		+C=−37
	2		2

C=−37 Równanie okręgu ma postać:

	1		3
x*2+y2−		x+		y−37=0
	4		2

Liczę współrzędne środka:

	A		−1/4		1
a=−		=−		=
	2		2		8

	B		3/2		3
b=−		=−		=−
	2		2		4

r=√a²+b²−C=√(1/8²+(−3/4)²+37}=√1/64+9/16+37=√1/64+36/64+2368/64=√2405/64 =√2405/8 Odp:

	1		3
S=(		, −		)
	8		4

Uff, naliczyłem się trochę, takie "nieładne" wyniki wyszły, wolałem sprawdzić, czy nie robię błędu. Ale to autor wymyslił takie dane. Pewnie zadanie pochodzi z książki "Matematyka z plusem" Gdanskiego Wydawnictwa Oświatowego? Bo w tych książkach to chyba z 80 % zadań jest na ułamkach, rzadko zdarzają cię całkowite albo łatwe do policzenia liczby.

Eta: Podaję inny sposób Skoro mamy wyznaczyć środek S okręgu opisanego , to nie musimy wyznaczać równania tego okręgu środek S pokrywa się z punktem przecięcia się symetralnych boków trójkąta Wyznaczam równania dwu symetralnych np: sym _AB i sym_AC

	−2+6		5−1
wyznaczamy środki odcinków AB : D(		,		) =D ( 2, 3)
	2		2

	6−6		1−1
AC: E({		,		)= E( 0,0)
	2		2

	5−1		−1
wyznaczamy wsp. kierunkowe prostych AB : aAB=		=
	−2−6		2

to symAB: y= 2( x−x_D) +y_D sym. AB: y= 2(x−2)+3 => symAB: y= 2x −1

	1+1		1
podobnie wsp. kierunkowy pr. AC : aAC=		=
	6+6		6

to sym. AC : y= −6(x−x_E)+y_E sym.AC: y= − 6x rozwiązując układ równań symetralnych otrzymujemy S y= −6x => 2x−1= −6x to x= ¹₈ i y= −6*¹₈= −³₄ y= 2x −1 odp: S( ¹₈, −³₄ Wynik taki sam jaki podał Gustlik

Eta: No to pora spać Dobranoc Bogdanie miłych snów

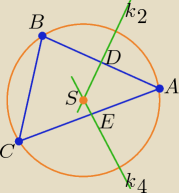
Bogdan: Proponuję następujące rozwiązanie. A = (6, 1), B = (−2, 5), C = (−6, −1), środek boku AB: D = (2, 3), środek boku AC: E = (0, 0), S − środek okręgu Wyznaczamy symetralne boków AB i AC. Ich punkt przecięcia jest szukanym punktem S.

	5 − 1		1
Prosta k1 zawierająca A, B: y = a1x + b1, a1 =		= −
	−2 − 6		2

Prosta k₂ zawierająca D, S: y = a₂x + b₂, k₂⊥k₁ ⇒ a₂ = 2, D = (2, 3) to y = 2(x − 2) + 3 ⇒ y = 2x − 1

	1 + 1		1
Prosta k3 zawierająca A, C: y = a3x + b3, a3 =		=		,
	6 + 6		6

Prosta k₄ zawierająca E, S: y = a₄x + b₄, k₄⊥k₃ ⇒ a₄ = −6, E = (0, 0) to y = −6x Wyznaczamy S rozwiązując układ równań: y = 2x − 1 i y = −6x

	1		1		3
2x − 1 = −6x ⇒ 8x = 1 ⇒ x =		, y = −6*		= −
	8		8		4

	1		3
Odp.: S = (		, −		)
	8		4

Bogdan: Tym razem Gustlik pojechał okrężną drogą Dobranoc

Gustlik: Szczerze mówiąc myślałem o tym sposobie. Pozdrawiam.

crazy nati: dzięki wielkie .....błagam pomóżcie rozwiązac to zadanie zamieszczone przeze mnie wczesniej o równoległoboku i trójkącie prostokątnym....

Bogdan: Co to znaczy "wcześniej"?, gdzie mamy szukać tego zadania? Wrzuć tu link do tego zadania wpisując trzy nawiasy [, za nimi nr strony, np. ta strona ma nr 55257, cały zapis zamykasz trzema nawiasami ]. W podglądzie nie zobaczysz tych kwadratowych nawiasów, nr strony będzie w kolorze niebieskim. Np. link do innego twojego zadania tak wygląda: 55256

crazy nati: 55227 Bogdan pomoz...

k;no;ijik;juipn: chyba miał ..........