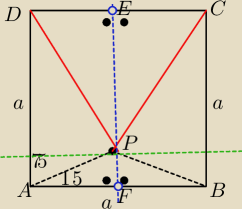
Kwadrat 6latek: Wewnątrz kwadratu ABCD dany jest punkt P taki że ∡PBA=∡PAB=15^o Udowodnij że trójkat CPD jest równoboczny Trójkąt APB jest trojkatem równoramiennym Stąd PF będzie wysokosćia tego trójkąta i jednocześnie przyprostokątna Δ prostokątnego AFP

	1
W trójkącie AFP AF=		a
	2

	|PF|
tg 15o=
	|AF|

|PF|= tg15^o*|AF|

	1		√3a
|PF|=		a(2−√3)=a−
	2		2

|EP|=|EF|−|PF|

	√3
|EP|=		a
	2

Stąd ΔDEP jest trójkatem prostokatnym o kątach 30 60 90^o ∡DPE=30^o ∡EDP=60^o i |DP|=|DC|a Z przystawania tropjkatów DPE i EPC wynika ze |CP|=|DP|=|DC|=a Więc trójkat DCP jest równoboczny

najukochańszy_z_ukochanych: brakuje mi wyjaśnienia −−− skąd wiesz, że tg15^o = 2 − √3

6latek: Odczytałem z tablic W sumie to pamietam bo niedawno ktoś tego potrzebował Ale moge sobie obliczyc tg(45^o−30^o) Zrobiłem w ten sposób ,ale autor oznaczył je jako trudne . Pewnie można też inaczej to zadanie rozwiążac bo autor dorysowuje jakies inne trójkąty

www: https://matematykaszkolna.pl/forum/370936.html

www: https://matematykaszkolna.pl/forum/357965.html Powodzenia

6latek: Oczywiście dziękuje

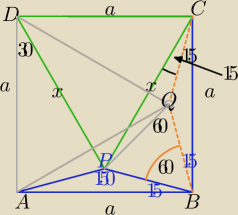
Mila: 1) |PB|=|BQ|⇒ΔPBQ− Δrównoboczny 2) |PQ|=|CQ|⇒ΔPCQ− Δrównoramienny ∡PQC=360^o−60^o−150^o=150^o ∡PCQ=15^o 3) ∡PCB=30^o=∡PDA to∡PDC=60^o =∡PCD⇔ 4) ΔDCP−Δrównoboczny uzupełnij komentarz, j czegoś Ci brakuje.

Mila: maiło być: jeśli

6latek: Dziękuje Milu Pozdrawiam

Mila: