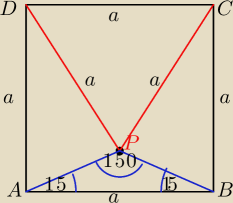
 Wewnatrz kwadratu ABCD dany jest punkt P taki ze kąt PBA= kątowi PAB =15o
Udowodnij ze trojkat CPD jest rownoboczny
Skoro ∡PAB=∡PBA to ΔAPB jest trojkatem rownoramiennym a to oznacza ze punkt P lezy na
symetralnej boku AB
I na tym sie moja inwencja tworcz w tym zadaniu konczy .
Wewnatrz kwadratu ABCD dany jest punkt P taki ze kąt PBA= kątowi PAB =15o
Udowodnij ze trojkat CPD jest rownoboczny
Skoro ∡PAB=∡PBA to ΔAPB jest trojkatem rownoramiennym a to oznacza ze punkt P lezy na
symetralnej boku AB
I na tym sie moja inwencja tworcz w tym zadaniu konczy .
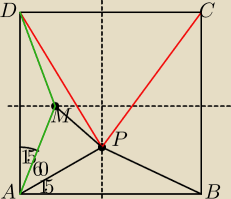 Kontynuujemy dalej
Skoro punkt P lezy na symetralnej boku AB to tak samo bedzie lezal na symetralnej boku CB lub
DA
Narysowalem na DA
Nie wiem dlaczego jest taka wskazowka zeby ten trojkat ADM narysowac
Z rownosci trojkatow ABP i ADM wynika ze (korzystam z odpowiedzi Milo w linku)
AM= AP i kąt MAP= 60 o
Teraz wedlug mnie wynika z tego ze trojkat AMP jest rownoramienny
Teraz jak mam pokazac ze ΔAMP jest rownoboczny czyli ze MP= AM= AP ?
I co mi da pokazanie ze ΔAMP jest rownoboczny ?
Kontynuujemy dalej
Skoro punkt P lezy na symetralnej boku AB to tak samo bedzie lezal na symetralnej boku CB lub
DA
Narysowalem na DA
Nie wiem dlaczego jest taka wskazowka zeby ten trojkat ADM narysowac
Z rownosci trojkatow ABP i ADM wynika ze (korzystam z odpowiedzi Milo w linku)
AM= AP i kąt MAP= 60 o
Teraz wedlug mnie wynika z tego ze trojkat AMP jest rownoramienny
Teraz jak mam pokazac ze ΔAMP jest rownoboczny czyli ze MP= AM= AP ?
I co mi da pokazanie ze ΔAMP jest rownoboczny ?

 Taka jest tresc zadania
Taka jest tresc zadania
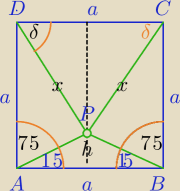 1) ΔABP− Δrównoramienny
|AP|=|BP|⇒|PD|=|PC|
2)
1) ΔABP− Δrównoramienny
|AP|=|BP|⇒|PD|=|PC|
2)
| h | ||
tg15= | ||
| 0.5a |
| a−0.5atg15 | ||
tgδ= | ⇔tgδ=2−tg15⇔tgδ=2−(2−√3) | |
| 0.5a |
 Jednak chcialbym to zrobic na trojkatach przystajacych .
Po prostu musze umiec zauwazac takie trojkaty .
Jednak chcialbym to zrobic na trojkatach przystajacych .
Po prostu musze umiec zauwazac takie trojkaty .
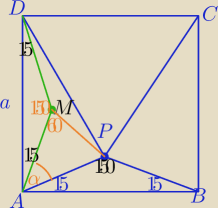 To wg wskazówki.
|AP|=|BP| i |PD|=|PC|
1) Na boku AD budujemy Δ ADM przystający do ΔABP.
2)
|∡MAP|=90−2*15=60⇔
ΔMPA− Δrównoboczny jako równoramienny o kącie 60 między ramionami.
3)|MP|=|AM|=|DM|
ΔDPM− Δrównoramienny
|∡DMP|=360−(150+60)=150⇔
ΔDPM≡ADM⇔|PD|=a=|PC|=|DC|
ΔDCP− Δrównoboczny.
To wg wskazówki.
|AP|=|BP| i |PD|=|PC|
1) Na boku AD budujemy Δ ADM przystający do ΔABP.
2)
|∡MAP|=90−2*15=60⇔
ΔMPA− Δrównoboczny jako równoramienny o kącie 60 między ramionami.
3)|MP|=|AM|=|DM|
ΔDPM− Δrównoramienny
|∡DMP|=360−(150+60)=150⇔
ΔDPM≡ADM⇔|PD|=a=|PC|=|DC|
ΔDCP− Δrównoboczny.



 Ale przy okazji dowiedzialem sie dlaczego ΔMPA jest rownoboczny(22 ; 36)
mam juz jeden kat MAP 60o i jesli trojkat jest rownoramienny a jest i jeden z katow ma 60o
(ma ) to taki trojkat jest rownoboczny
Ale przy okazji dowiedzialem sie dlaczego ΔMPA jest rownoboczny(22 ; 36)
mam juz jeden kat MAP 60o i jesli trojkat jest rownoramienny a jest i jeden z katow ma 60o
(ma ) to taki trojkat jest rownoboczny