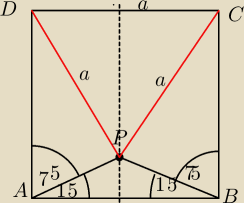
Kwadrat i punkt wewnatrz 5-latek: Wewnatrz kwadratu ABCD dany jest punkt P taki ze kat PAB= k atowi PBA=156o Udowodnij z etrojkat CPD jest rownoboczny Zeby te katy podane w zadaniu mialy miare 15^o to punkt P musi lezec na symetralnej odcinka AB (wynika to z wlasnisci trojkata rownoramiennego Ta symterallna dzieli bok DC na dwie rowne czesci mamy udowodnic ze DC= DP=CP

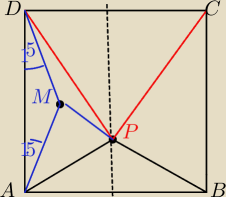
5-latek: Zadanie jest oznaczone jako bardzo trudne We wskazowce pisza zeby narysowac trojkat ADM przystajacy do APB

Milo: Z przystawania ΔDAM i ΔPAB mamy |AM| = |AP| Dodatkowo na kątach łatwo policzyć, że |∡MAP| = 60^o Stąd ΔMAP jest równoboczny |∡DMP| = 360^o − 150^o − 60^o = 150^o = |∡DMA| oraz (z naszego trójkąta równobocznego) |MP| = |AM| z zasaby kbk ΔDMA ≡ ΔDMP W szczególności |DP| = |DA| Więc oczywiście też |DP| = |DC| Że |DP| = |CP| można łatwo udowodnić z przystawania ΔAPD i ΔBPC (|AP|=|BP|, kąt 75^o i |AD|=|BC|) Mam nadzieję, że się nigdzie nie pomyliłem przez późną porę

5-latek: Witam Sprawdze pozniej te obliczenia . jednak bardziej nurtuje mnie to jak wpasc na to zeby dorysowac ten trojkat bez tej wskazowki

Milo: Poprawka: ΔDMA≡ΔDMP z bkb (wspólny bok DM, kąty 105^o i |AM| = |MP|)

Milo: Poprawka do poprawki − kąty 150^o... A naprawdę nie mam pojęcia, jak wpaść na dorysowanie tego trójkąta

Milo: To ja już lepiej pójdę spać, dobranoc

5-latek: Dobranoc ja sie domslam z tym kątem 150^o

Adamm:

	a		a
a=		*tg15o+		*tgα
	2		2

tg15^o=2−√3 tgα=2−tg15^o=√3 α=60^o

Adamm: α to kąt CDP (zapomniałem dodać)

LWG: P musi leżeć na symetralnej odcinków AB i CD. Wtedy |EP|=a√3/2. E dzieli CD na połowę. F dzieli AB na połowę. |FP|=(atg15⁰)/2. |EP|=(a−atg15⁰)/2. Zatem 1−(tg15⁰)/2=√3/2. c.n.w.

5-latek: dziekuje Adamm i LWG