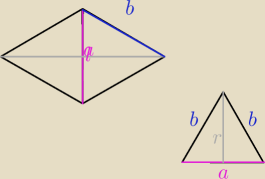
Obwód trójkąta równoramiennego jest równy L. Jakie długości powinny mieć boki tego trójkąta,
aby objętość bryły powstałej w wyniku obrotu wzdłuż podstawy była największa?
V−>max
V=2*13 π * r2 * a2
L=a+2b
b=L−a2
r2 + (a2)2 = (L−a2)2
r2 = (L−a)24 − a24
r2 = L2−2La+a2−a24
r2 = L2−2La4 ∧ r > 0
r = √L2−2La2
V(a) = 2*13 π * L2−2La4 * a2
V(a)=π12 * (L2 a − 2La2)
V'(a)=
nie mam pojęcia jak wyznaczyć dziedzinę i w sumie jak to dalej policzyć
| a+b | ||
L= | =>b=L/2−a/2=>b∊(0,L/2) | |
| 2 |
| L | ||
L=0 v a= | =>Vm | |
| 4 |
| a+b | ||
L= | ?  | |
| 2 |
| π | ||
V(a) = | *[ L2 a − 2 a 2 L ] | |
| 12 |
| π | ||
V '(a) = | *[ L2 − 4a*L] = 0 ⇔ L2 − 4a*L= 0 | |
| 12 |
| 1 | ||
a = | L | |
| 4 |
| 1 | ||
Dla a < | L jest V '(a) > 0 | |
| 4 |
| 1 | ||
Dla a > | L jest V '(a) < 0 | |
| 4 |
| L | ||
zatem dla a = | objętość jest największa. | |
| 4 |
| L | 3 | |||
2 b = L − a = L − | = | L | ||
| 4 | 4 |
| 3 | ||
b = | L | |
| 8 |
