Geometria
Werve: Dany jest trójkąt prostokątny o przyprostokątnych długości 13 i 27. Oblicz długość odcinka
dwusiecznej kąta prostego, zawartego w danym trójkącie. Wynik podaj z dokładnością jednej
setnej.
15 lut 08:08
getin:
przeciwprostokątna c = √132+272 = √898
Rozwiąż układ równań
{y2 = 132 + x2 − 26x*cos45o
{(√898−y)2 = 272 + x2 − 54x*cos45o
Wyliczona wartość x będzie odpowiedzią do zadania
15 lut 08:30
15 lut 08:41
Werve: Przepraszam że pytam ale co to y i x
15 lut 08:41
Werve: Never mind
15 lut 08:42
15 lut 08:55
daras:
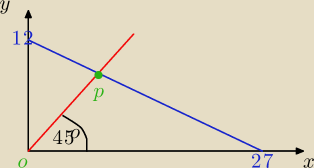 y = x
y = x
15 lut 09:01
Eta:
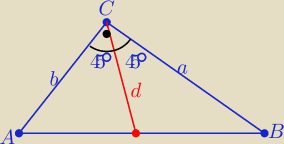 ===========
===========
Podstaw dane i oblicz............
15 lut 10:40
Eta:
| | ab | | bd | | ad | |
P(ABC)= |
| P1= |
| *sin45o , P2= |
| *sin45o |
| | 2 | | 2 | | 2 | |
P(ABC)=P
1+P
2
============
15 lut 10:48
daras: mój "analityczny" sposób jest jednak najprostszy

nie trzeba wcale znać wielu wzorów, własciwie tylko tw. Pitagorasa
15 lut 13:50
Eta:

15 lut 13:56
Eta:
A jak ktoś nie zna Pitagorasa

15 lut 13:58
chichi:
A ty @
Eta jak go znasz, to pozdrów go ode mnie

15 lut 14:01
Eta:
Masz to..... jak w ruskim banku

15 lut 14:04
daras: ode mnie też

15 lut 14:30
daras: może zaproś go na to forum

15 lut 14:30


 nie trzeba wcale znać wielu wzorów, własciwie tylko tw. Pitagorasa
nie trzeba wcale znać wielu wzorów, własciwie tylko tw. Pitagorasa





