Prawdopodobieństwo, zakres rozszerzony
Damian#UDM: Prawdopodobieństwo PR
(0 – 4) Dane są urny typu U
1i typu U
2, przy czym urn typu U
2 jest o dwie mniej niż urn typu
U
1. Wszystkie urny danego typu zawierają same kule w takich samych kolorach.
Prawdopodobieństwo wylosowania kuli białej z U
1 jest równe 0,25 , natomiast
prawdopodobieństwo wylosowania kuli białej z U
2 jest równe 0,25. Prawdopodobieństwo
wylosowania kuli białej z losowo wybranej urny jest równe 0,22. Wyznacz liczbę wszystkich urn.
(0 – 4) Ze zbioru liczb {1,2,3,…,6n+3} losujemy jedną liczbę. Niech A
n oznacza zdarzenie, że
otrzymamy liczbę podzielną przez 2 lub podzielną przez 3. Oblicz granicę lim┬(n→
∞)P(A
n ) .
Zapraszam do wspólnych przemyśleń i rozwiązań. Mam na to jakieś pomysły lecz proszę o wasze

5 lut 16:55
Saizou :
Zad. 2
| | 6n+3 | |
Liczb podzielnych przez 2 w tym zbiorze jest: [ |
| ] = 3n+1 |
| | 2 | |
| | 6n+3 | |
Liczb podzielnych przez 3 w tym zbiorze jest: [ |
| ] = 2n+1 |
| | 3 | |
| | 6n+3 | |
Liczb podzielnych przez 6 w tym zbiorze jest: [ |
| ] = n |
| | 6 | |
A
n = 3n+1+2n+1−n = 4n+2
| | 4n+2 | | 2 | |
P(An) = |
| → |
| , gdy n → +∞ |
| | 6n+3 | | 3 | |
5 lut 18:43
Damian#UDM: | | 6n+3 | |
Saizou ten zapis na przykład [ |
| ] to symbol Newtona? |
| | 2 | |
6 lut 00:57
Saizou : Nie, to cześć całkowita liczby.
6 lut 08:51
Damian#UDM: ok, dziękuję

Czy ktoś ma pomysł na 1. zadanie?
14 lut 11:04
Damian#UDM:
3. (0 – 3) Doświadczenie losowe polega na siedmiokrotnym rzucie kostką do gry. Oblicz
prawdopodobieństwo zdarzenia, że iloczyn oczek jest równy 12.
4. (0 – 4) Doświadczenie polega na sześciokrotnym rzucie sześcienną kostką do gry. Oblicz
prawdopodobieństwo zdarzenia, że dokładnie cztery razy z rzędu wypadnie taka sama liczba
oczek.
6. (0 – 4) Oblicz ile elementów ma zbiór, który ma 37 wszystkich podzbiorów o co najwyżej 2
elementach.
14 lut 11:07
Qulka: na pewno w obu pr−wo jest 0.25

14 lut 11:07
Damian#UDM: już sprawdzam Qulka
14 lut 11:09
Qulka: wstaw cyferki właściwe
| n | | n−2 | |
| •pr1+ |
| •pr2=pr że biała |
| 2n−2 | | 2n−2 | |
policz n wszystkich urn jest 2n−2
14 lut 11:09
Damian#UDM: Mój błąd, przepraszam

Podaje poprawną treść zadania:
(0 – 4) Dane są urny typu U1 i typu U2, przy czym urn typu U2 jest o dwie mniej niż urn typu
U1. Wszystkie urny danego typu zawierają same kule w takich samych kolorach.
Prawdopodobieństwo wylosowania kuli białej z U1 jest równe 0,2 , natomiast
prawdopodobieństwo wylosowania kuli białej z U2 jest równe 0,25. Prawdopodobieństwo
wylosowania kuli białej z losowo wybranej urny jest równe 0,22. Wyznacz liczbę wszystkich urn.
14 lut 11:12
Qulka: to jeszcze raz pisać wzór czy policzysz? bo nie skopiowałam tych ułamków?
14 lut 11:23
Damian#UDM: Spróbuję sam, dziękuję

14 lut 11:30
kerajs:
3)
(2,6,1,1,1,1,1), (3,4,1,1,1,1,1), (2,2,3,1,1,1,1)
4)
| | 6*1*1*1*5*6+6*5*1*1*1*5+6*6*5*1*1*1 | |
P= |
| |
| | 66 | |
5)
n=8
14 lut 12:09
Mila:
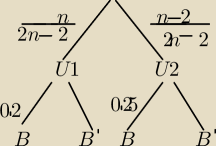
Zadanie 1)
| | n | | n−2 | |
P(B)= |
| *0.2+ |
| *0.25 |
| | 2n−2 | | 2n−2 | |
n=6− liczba urn typu U1
4− liczba urn typu U2
6+4=10
14 lut 20:20
Damian#UDM: Dziękuje wam za pomoc
 Qulka
Qulka rozumiem, że w tym zadaniu wystarczyło skorzystać ze wzoru na prawdopodobieństwo
całkowite oraz określić naszą niewiadomą, a tego drugiego już mi się nie udało.
kerajs jeśli chodzi o Twoje rozwiązania to niestety nic z tego prawie nie rozumiem.
w 5) do rozwiązania zabrakło mi jedynie 1, a to wynika chyba z tego, że nie wziąłem pod uwagi
możliwości, że ten zbiór może mieć podzbiory, które nie mają elementów, więc wydaje mi się, że
z tego to 1 wynika

3) rozumiem rozbicie 12 na iloczyn siedmiu liczb i z tego mamy trzy możliwości, lecz moc zbioru
A już niestety nie rozumiem.
Moim błędem na pewno było to, że rozróżniałem na przykład 2 i 6 i liczyłem zdarzenie za pomocą
wariancji bez powtórzeń, nadal nie rozumiem czemu to myślenie jest błędne.
Jak policzę za pomocą kombinacji to rozumiem, że wtedy wybieramy 2 elementy z 7 i nie obchodzi
| | 7! | |
mnie kolejność, lecz jak ja to zapisuje to mam |
| a u Ciebie tej dwójki brakuje. |
| | 2!*5! | |
W możliwości (2,2,3,1,1,1,1) rozumiem, że wybieramy trzy elementy z siedmiu i nie obchodzi mnie
| | 7! | |
też kolejność, tylko znowu u mnie wychodzi |
| , a nie jak u Ciebie 2! |
| | 3!*4! | |
Więc niestety nie rozumiem skąd to wynika. Proszę o wytłumaczenie

4) Nie mam pojęcia skąd ta moc zbioru A, proszę o wyjaśnienie, zależy mi na tym, żeby to
zrozumieć

14 lut 20:26
Saizou :
3)
Układ (2,6,1,1,1,1,1).
Wszystkich permutacji tego zbioru jest 7!, jednak my nie rozróżniamy jedynek, dlatego
musimy podzielić 7! przez liczbę permutacji zbioru (1a, 1b, 1c, 1d, 1e), zatem jest ich
Układ (3,4,1,1,1,1,1) − analogicznie
Układ (2,2,3,1,1,1,1)
Wszystkich permutacji jest 7!
Permutacji zbioru (2a, 2b) jest 2!
| | 7! | |
Permutacji zbioru (1a, 1b, 1c, 1d) jest 4!, zatem mamy |
| |
| | 2!*4! | |
Wszystkich możliwych ciągów jest 6
7
14 lut 20:35
Damian#UDM: Saizou bardzo dziękuję za wytłumaczenie tego zjawiska.
Właśnie chyba zrozumiałem o co chodzi

Normalnie z permutacji liczymy jakby wszystko było różne, lecz jedynki nie są i musimy
podzielić przez permutacje rozróżnialnych jedynek (które nie istnieją) i tak samo z dwójkami i
pomnożyć z jedynkami na dole tam gdzie trzeba.
Świetny pomysł.
Co do 4)
Rozumiem to tak, że mamy 6 możliwości:
1.* (1,1,1,1,x,y)
2.* (2,2,2,2,k,m)
3.* (3,3,3,3,a,b)
4.* (4,4,4,4,c,d)
5.* (5,5,5,5,g,h)
6.* (6,6,6,6,p,r)
mam 6 miejsc więc 3 możliwości ustawienia w każdym powyższym zdarzeniu:
x x x x _
xxxx_
xxxx
i liczby x,y,k,m,a,b,c,d,g,h,p,r muszą się różnić od tych w ich danym zdarzeniu.
więc mógłbym to chyba policzyć tak:
6*3*1*1*1*1*5*5
I to myślenie pewnie jest źle, nie wiem czemu

Proszę o pomoc.
14 lut 23:09
Damian#UDM: Dziękuję
Milu za pomoc, pozdrawiam ciepło

14 lut 23:09
Saizou :
Zad. 4
Możliwe układy to
1) (aaaabc)
• a wybieramy na 6 sposobów
• b wybieramy na 5 sposobów (nie może być taka sama jak a)
• c wybieramy na 6 sposobów
Razem: 6*5*1*1*1*6
2) (baaaac)
• b wybieramy na 6 sposobów
• a wybieramy na 5 sposobów (nie może być taka sama jak b)
• c wybieramy na 5 sposobów (nie może być taka sama jak a)
Razem: 6*5*1*1*1*5
3) (bcaaaa)
• b wybieramy na 6 sposobów
• c wybieramy na 6 sposobów
• a wybieramy na 5 sposobów (nie może być taka sama jak c)
Razem: 6*6*5*1*1*1
U ciebie np.
(1, 1, 1, 1, x, y)
x musi być różny od 1, ale już y jest dowolny
15 lut 09:34
kerajs: Ad powyższy post:
Oczywiście tylko pierwszy ''a'' wybierany jest na tyle sposobów. Kolejne ''a'' muszą być takie
same jak pierwszy, więc wybierane są tylko na 1 sposób, i stąd te jedynki w iloczynach.
Ad 3)
ilość zdarzeń sprzyjających można także obliczyć z kombinacji:
Przykładowo, dla układu (2,6,1,1,1,1,1) wybierasz 5 miejsc (z 7) dla jedynek, i miejsce dla
dwójki (szóstka musi zająć jedyne wolne miejsce)
albo wybierasz 5 miejsc (z 7) dla jedynek, miejsce dla dwójki i miejsce dla szóstki
Kolejność wyboru nie ma znaczenia:
Wybierasz miejsce dla szóstki, 5 miejsc (z 7) dla jedynek i miejsce dla dwójki
albo
Wybierasz miejsce dla szóstki, dla dwójki i 5 miejsc (z 7) dla jedynek
Sprawdź, czy zawsze dostaniesz ten sam wynik.
PS
Dziwi mnie spora różnica poziomów między zakładanymi przez Ciebie tematami. Jesteś licealistą
który, z niezrozumiałych dla mnie powodów, chce rozwiązywać równania różniczkowe, czy
absolwentem szkoły średniej uzupełniającym braki?
15 lut 10:26
Damian#UDM: Dziękuję
saizou za objaśnienie zadania 4. Teraz rozumiem moje błędne myślenie

Zakładałem, że jak mają być 4 pod rząd takie same to już nigdzie indziej taka sama nie może
się pojawić i to było błędne myślenie − przede wszystkim.
Dziękuję
kerajs za objaśnienie zadania 3. Zrobiłem je wcześniej sam i w ten sposób, że jak
mam na przykład dla przykładu 6*2*1*1*1*1*1 mam siedem miejsc to miejsce dla 6 mogę wybrać na
| | | |
7 sposobów, a miejsce dla 2 na 6 sposobów, a dla jedynek z dwumianu Newtona wychodzi | . |
| | |
Dla reszty przypadków zrobiłem w podobny sposób i widzę, że moje myślenie nie było złe.
Dostałem te zadania od jednego ucznia i niestety zauważyłem, że mam z niektórymi problem, a
chciałbym pomagać innym w matematyce jak najlepiej umiem, dlatego zgłaszam się z większością
spraw tutaj bo wiem, że wiedzą i doświadczeniem
Eta Mila Mariusz kerajs
Qulka saizou ICSP wreduluspospolitus Jerzy jesteście kilkanaście
leveli wyżej niż ja i cieszę się, że mogę na was liczyć.
Bardzo to doceniam

Dziękuję wam.
Co do mnie to w tym roku po raz 6. przystępuje do matury rozszerzonej z matematyki ponieważ
moim małym marzeniem jest 100%, a brakuje mi już niewiele, bo tylko 1 punkt.
Zostawiam link poniżej do postu z wglądem do mojego arkusza oraz zadania, w którym dostałem
jeden punkt mniej:
https://matematykaszkolna.pl/forum/403637.html
Jak ktoś ma jakieś przemyślenia co do mojego rozwiązania to zapraszam. Odwoływałem się do OKE,
gdzie dostałem 2% więcej za nie uznanie przez nich wyznaczenia przeze mnie największej
wartości. Z dziedziną odwoływałem się do kolegium arbitrażu egzaminacyjnego, niestety bez
skutku. Szkoda, że trzy znaki x<y tyle zmieniły.
Czuję, że to będzie w tym roku, łatwiej już nigdy nie będzie

Materiał ze studiów chce się nauczyć, ponieważ chce go umieć i móc pomagać z nim innym:
pochodne, całki, szeregi, równania różniczkowe, płaszczyzny, funkcje dwóch, trzech zmiennych,
granice oraz płaszczyzny.
Jak to będę ogarniał to będzie super, ale oczywiście najpierw 100% z PR.
Szeregów, równań różniczkowych, funkcji trzech zmiennych w ogóle nie umiem, a płaszczyzny
bardzo słabo. Tym się na pewno zajmę w przyszłości, a niedługo chciałbym zobaczyć czy na
przykład szeregi jestem w stanie ogarnąć szybko.
Matematyka łatwo mi przychodzi i dużo zagadnień sam się nauczyłem. Więc ciągnę to dalej z
sukcesami. Lubię matematykę. Matma jest super.
Dziękuję za waszą pomoc, fajnie, że tu jesteście

16 lut 00:49
Damian#UDM: Zadań z prawdopodobieństwa ciąg dalszy

6. (0 – 4) Dwóch strzelców oddało po jednym strzale do tego samego celu. Oblicz
prawdopodobieństwo, że pierwszy z nich trafił, jeśli wiadomo, że cel został trafiony tylko
jeden raz. Zakładamy, że prawdopodobieństwo trafienia w cel jest równe dla pierwszego strzelca
9/10, a dla drugiego wynosi 3/4.
7. (0 – 4) Wykaż, że jeśli P(A│C) = P(A│C
' ), gdzie P(C)>0 i P(C
' )>0 to zdarzenia A oraz C
są niezależne.
27 lut 18:13
ite: A może być podpowiedź?
27 lut 18:32
Damian#UDM: jasne, że tak

Każda pomoc jest dobra

27 lut 19:44
Damian#UDM: P(A/C) = P(A∩C') = P(A) − P(A∩C)
27 lut 19:53
Damian#UDM: I po przekształceniach wychodzi mi P(A∩C) = P(A)*P(C), co oznacza, że zdarzenia są niezależne,
tak samo jak pierwszy rzut kostką oraz drugi rzut kostką.
Chyba rozumiem 7. (0 − 4)

27 lut 19:56
Mila:
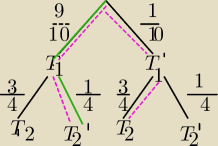
6)
T− cel trafiony jeden raz
| | 9 | | 1 | | 1 | | 3 | | 9+3 | | 12 | | 3 | |
P(T)= |
| * |
| + |
| * |
| = |
| = |
| = |
| |
| | 10 | | 4 | | 10 | | 4 | | 40 | | 40 | | 10 | |
27 lut 20:13
Eta:
I (T
1, N
2)
II (N
1, T
2)
Cel trafiony tylko raz
P(T)= 0,9*0,25+0,1*0,75= 0,3
Cel trafiony tylko przez I
P(T
1)=0,9*0,25=0,225
27 lut 20:23
Damian#UDM: Tak myślałem o prawdopodobieństwie warunkowym oraz całkowitym, lecz nie umiałem do tego dojść.
Dziękuję
Milu za pomoc!

27 lut 20:24
Damian#UDM: Oraz dziękuję Eta, jesteście wspaniałe!
27 lut 20:24
Eta:
Nie Wszyscy tak myślą

Miłe to...... .......

27 lut 20:26
Eta:
Napisałam dlatego drugi sposób, bo .. ( nie lubię "krzaków" )

27 lut 20:28
Damian#UDM: Ja cieszę się z każdego poprawnego rozwiązania

Każde poprawne rozwiązanie uczy i daje do
myślenia

27 lut 21:04
Damian#UDM: (0−1)
Rzucamy dwiema symetrycznymi sześciennymi kostkami do gry. Liczba kombinacji, że na obu
kostkach wypadła liczba oczek nie większa niż 4 to:
A. 36 B. 9 C. 16 D. 4
Nie mogę zrozumieć, czy na obu kostkach w sumie nie może być więcej oczek niż 4, czy na każdej
kostce ma być nie więcej niż 4 oczka.
28 lut 01:46
Damian#UDM: Jeżeli mój drugi wariant jest poprawny to wtedy odpowiedź C.
28 lut 01:46
Damian#UDM: A jeżeli pierwszy wariant to odpowiedź D.
28 lut 01:47
Qulka: na każdej kostce oddzielnie
28 lut 09:50
kerajs: Akurat fragment ''na obu kostkach wypadła liczba oczek nie większa niż 4 '' jest jednoznaczny,
czyli ''na każdej kostce ma być nie więcej niż 4 oczka''.
Prawdziwym problemem jest niefortunna ''Liczba kombinacji'' która w języku potocznym oznacza
liczbę układów (wtedy jest ich 16) , jednak w kombinatoryce kombinacja pomija kolejność (czyli
10).
28 lut 09:51
Damian#UDM: Rozumiem, dziękuję za pomoc

28 lut 12:35
Damian#UDM: 9. (0−5) PR NE 2021 2
Ze zbioru wszystkich liczb sześciocyfrowych większych niż 222000, w których zapisie dziesiętnym
mogą wystąpić tylko cyfry ze zbioru {1,2,3} losujemy jedną liczbę. Oblicz prawdopodobieństwo
zdarzenia A, polegającego na wylosowaniu liczby, w której zapisie każde dwie sąsiednie cyfry
będą
różniły się o 1.
|Ω| =
1. 22 na cyfrach setek oraz dziesiątek tysięcy oraz 2 możliwości wyboru cyfry tysięcy ze zbioru
{2,3} oraz 3x3x3 możliwości wyboru liczby spośród {1,2,3} = 2*27=54
2. 2 na cyfrze s.t. oraz 3 na cyfrze d.t. oraz 3x3x3x3 możliwości wyboru cyfry ze zbioru
{1,2,3} = 3
4 = 81
3. 3 na cyfrze s.t. oraz 3x3x3x3x3 możliwości wyboru cyfry ze zbioru {1,2,3} = 3
5 = 243
|Ω| = 1. + 2. + 3. = 378
A − sąsiednie cyfry różnią się o 1
po własnych przemyśleniach wnioskuje, że takich liczb jest zaledwie kilka

Wypisałem takie
możliwości:
232121
232123
232321
232323
321212
321232
323212
323232
Jeśli niczego nie przeoczyłem to |A| = 8
| | 8 | | 4 | |
Wtedy P(A) = |
| = |
| |
| | 378 | | 189 | |
Czy jest ok?
1 mar 01:48
kerajs: Wynik jest dobry.
Szukając zdarzenia sprzyjające można zauważyć iż co drugą cyfrą musi być 2.
''|Ω| = 1. + 2. + 3. = 378''
Przez takie dziwne zapisy traci się punkty. Moim zdaniem poprawianie matury jest mało sensowne
jeśli nie jest związanie z przyjęciem na wymarzony kierunek studiów.
1 mar 14:14
Damian#UDM: No to super, dziękuję za sprawdzenie

To jaki zapis
kerajs proponujesz, żeby był on poprawny?
Już mam opłacony egzamin więc na pewno do niego podejdę

Trzeba jeszcze wiedzieć co chce się w życiu robić, a ja tego jeszcze raczej nadal szukam.
Ale dziękuję za przemyślenia. 100% zdobędę w tym roku i już koniec mojej przygody z maturami

1 mar 14:21
Damian#UDM: 2. (0−1) CKE Próbna 2021 PR
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej
jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne.
Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była
czarna. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z pierwszej z tych
urn, jest równe
Proszę o pomoc

Nie wychodzi mi

10 mar 13:21
Damian#UDM: Dobra, już chyba wiem

C − wylosowano kule czarną
| | 1 | | 3 | | 1 | | 2 | | 23 | |
P(C) = |
| * |
| + |
| * |
| = |
| |
| | 2 | | 8 | | 2 | | 10 | | 80 | |
C|B1 − wylosowano kulę czarną z Urny 1
B1 − wylosowano Urnę 1
| | 1 | | 3 | | 3 | |
P(B1)*P(C|B1)= |
| * |
| = |
| |
| | 2 | | 8 | | 16 | |
| P(B1)*P(C|B1)) | | 316 | | 15 | |
| = |
| = |
| |
| P(C) | | 2380 | | 23 | |
Czy to jest poprawne rozwiązanie?
10 mar 13:28
Damian#UDM: To jest, że kula czarna pochodzi z urny drugiej, dla urny pierwszej będzie chyba inaczej

10 mar 13:32
ite:
| pr−stwo k.czarnej z pierwszej urny | |
| |
| pr−stwo k.czarnej z I urny+pr−stwo k.czarnej z II urny | |
nie wiem, czy to jest czytelne:
pr−stwo k.czarnej z pierwszej urny oznacza
prawdopodobieństwo wylosowania kuli czarnej z pierwszej urny
10 mar 13:46
Mila:
Damian narysuj drzewko, wszystko zobaczysz.
10 mar 21:06
al:
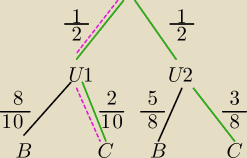
...
10 mar 21:32
Damian#UDM: Dziękuje wam wszystkim za pomoc!

17 mar 22:43
Damian#UDM: 11. PR
W każdej z trzech urn znajduje się 5 kul. W pierwszej urnie: 4 białe i 1 czarna, w drugiej
urnie: 2 białe i 3 zielone, a w trzeciej urnie: 3 zielone i 2 czarne. Z każdej urny losujemy
po jednej kuli i nie oglądając jej, wkładamy do czwartej, pustej urny. Następnie z tej urny
losujemy jedną kulę. Oblicz prawdopodobieństwo zdarzenia, że w wyniku takiego doświadczenia
wylosowana z czwartej urny kula będzie zielona.
17 mar 22:47
18 mar 01:19
Eta:
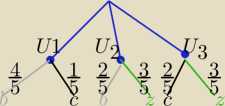
1 zielona w urnie U
4 gdy:
(b,b,z) (b,z,c) (c,b,z) (c,z,c)
2 zielone w U
4 gdy:
(b,z,z) ( c,z,z)
| | 1 | | 4 | | 2 | | 3 | | 4 | | 3 | | 2 | | 1 | | 2 | | 3 | |
P(1z)= |
| ( |
| * |
| * |
| + |
| * |
| * |
| + |
| * |
| * |
| + |
| | 3 | | 5 | | 5 | | 5 | | 5 | | 5 | | 5 | | 5 | | 5 | | 5 | |
| | 1 | | 3 | | 2 | | 60 | |
+ |
| * |
| * |
| ) =........... = |
| |
| | 5 | | 5 | | 5 | | 3*125 | |
| | 2 | | 4 | | 3 | | 3 | | 1 | | 3 | | 3 | | 90 | |
P(2z)= |
| ( |
| * |
| * |
| + |
| * |
| * |
| )=.... |
| |
| | 3 | | 5 | | 5 | | 5 | | 5 | | 5 | | 5 | | 3*125 | |
=========
18 mar 02:15
Eta:

20 mar 19:38
Damian#UDM: Rozpisałem sobie dokładnie tak samo zdarzenia, lecz nie potrafiłem policzyć tego
prawdopodobieństwa.
Dziękuję
Eta za pomoc

20 mar 23:03
Damian#UDM: 13. (0 − 5) ZI 2021 PR III
Z pudełka, w którym jest 13 kul ponumerowanych kolejnymi liczbami od 1 do 13, losujemy
bez zwracania 5 kul. Oblicz, jakie jest prawdopodobieństwo, ze wśród wylosowanych kul
jest dokładnie jedna para kul z sumą numerów równą 14.
Ω={1,2,3,4,5,6,7,8,9,10,11,12,13}
Ω − jak nazwać to zdarzenie? Pięcioelementowe kombinacje ze zbioru trzynastoelementowego?
A − wśród wylosowanych kul jest dokładnie jedna para kul z sumą numerów równą 14.
Możliwe pary:
{(1,13)(2,12)(3,11)(4,10)(5,9)(6,8)}
W tych pięciu elementach może być jedna z wyżej wymienionych par oraz trzy różne liczby z
trzech różnych par?
Tutaj moje pomysły się kończą.
Proszę o pomoc

20 mar 23:10
20 mar 23:20
Damian#UDM: Podziwiam was
Eta oraz
Mila za taką wiedzę z geometrii płaskiej oraz
prawdopodobieństwa

Jak można to tak ogarniać, też bym chciał

20 mar 23:27
Damian#UDM: (0 − 5) PR
Ze zbioru liczb {1,2,3,...,2n+1} losujemy kolejno trzy liczby bez zwracania i sumujemy je.
Oblicz liczbę elementów tego zbioru, wiedząc, że prawdopodobieństwo wylosowania trzech liczb,
| | 73 | |
których suma jest liczbą parzystą, jest równe |
| . |
| | 143 | |
Moje BŁĘDNE rozwiązanie:
Ω={1,2,3,...,2n+1}
Ω − trzy elementowe kombinacje ze zbioru (2n+1)−elementowego
| | | | (2n−1)*2n*(2n+1) | | | |
|Ω|= | = |
| = |
| |
| | | 6 | | 6 | |
|A|=|A
1|+|A
2|
A
1 − suma dwóch liczb nieparzystych oraz jednej liczby parzystej.
A
2 − suma trzech liczb parzystych.
| | | | 2n*(2n−1)(2n−2) | | 8n3−12n2+4n | |
|A2|= | = |
| = |
| |
| | | 6 | | 6 | |
| 2n*(16n2+2)6 | | 73 | | 16n2+2 | | 73 | |
| = |
| ⇔ |
| = |
| |
| 2n*(4n2−1)6 | | 143 | | 4n2−1 | | 143 | |
I z tego wychodzi
1996n
2 + 359 = 0
Gdzie znajduje się moje błędne myślenie? Proszę o pomoc

21 mar 23:54
Damian#UDM: Teraz tak patrzę i widzę, że omega dla n=6 jest równa 143, lecz ze zbiorem A już się nie zgadza

22 mar 00:20
Eta:
W tym zbiorze mamy : n liczb parzystych i n+1 liczb nieparzystych
|Ω|= (2n+1)*2n*(2n−1)= 2n(4n2−1)
A1 : (P,P,P) |A1|= n*(n−1)*(n−2)
A2: (P,N,N) (NPN) ( NNP)
|A2|= 3*n(n+1)*n
|A|= n(n−1)(n−2)+3n(n+1)*n
P(A) = 73/143
.................
............
n2=36 ⇒ n=6
=====
22 mar 00:30
Damian#UDM: Okej, teraz rozumiem mój błąd. Dziękuję

22 mar 01:05

 Czy ktoś ma pomysł na 1. zadanie?
Czy ktoś ma pomysł na 1. zadanie?

 Podaje poprawną treść zadania:
(0 – 4) Dane są urny typu U1 i typu U2, przy czym urn typu U2 jest o dwie mniej niż urn typu
U1. Wszystkie urny danego typu zawierają same kule w takich samych kolorach.
Prawdopodobieństwo wylosowania kuli białej z U1 jest równe 0,2 , natomiast
prawdopodobieństwo wylosowania kuli białej z U2 jest równe 0,25. Prawdopodobieństwo
wylosowania kuli białej z losowo wybranej urny jest równe 0,22. Wyznacz liczbę wszystkich urn.
Podaje poprawną treść zadania:
(0 – 4) Dane są urny typu U1 i typu U2, przy czym urn typu U2 jest o dwie mniej niż urn typu
U1. Wszystkie urny danego typu zawierają same kule w takich samych kolorach.
Prawdopodobieństwo wylosowania kuli białej z U1 jest równe 0,2 , natomiast
prawdopodobieństwo wylosowania kuli białej z U2 jest równe 0,25. Prawdopodobieństwo
wylosowania kuli białej z losowo wybranej urny jest równe 0,22. Wyznacz liczbę wszystkich urn.

 Zadanie 1)
Zadanie 1)
 Qulka rozumiem, że w tym zadaniu wystarczyło skorzystać ze wzoru na prawdopodobieństwo
całkowite oraz określić naszą niewiadomą, a tego drugiego już mi się nie udało.
kerajs jeśli chodzi o Twoje rozwiązania to niestety nic z tego prawie nie rozumiem.
w 5) do rozwiązania zabrakło mi jedynie 1, a to wynika chyba z tego, że nie wziąłem pod uwagi
możliwości, że ten zbiór może mieć podzbiory, które nie mają elementów, więc wydaje mi się, że
z tego to 1 wynika
Qulka rozumiem, że w tym zadaniu wystarczyło skorzystać ze wzoru na prawdopodobieństwo
całkowite oraz określić naszą niewiadomą, a tego drugiego już mi się nie udało.
kerajs jeśli chodzi o Twoje rozwiązania to niestety nic z tego prawie nie rozumiem.
w 5) do rozwiązania zabrakło mi jedynie 1, a to wynika chyba z tego, że nie wziąłem pod uwagi
możliwości, że ten zbiór może mieć podzbiory, które nie mają elementów, więc wydaje mi się, że
z tego to 1 wynika  3) rozumiem rozbicie 12 na iloczyn siedmiu liczb i z tego mamy trzy możliwości, lecz moc zbioru
A już niestety nie rozumiem.
Moim błędem na pewno było to, że rozróżniałem na przykład 2 i 6 i liczyłem zdarzenie za pomocą
wariancji bez powtórzeń, nadal nie rozumiem czemu to myślenie jest błędne.
Jak policzę za pomocą kombinacji to rozumiem, że wtedy wybieramy 2 elementy z 7 i nie obchodzi
3) rozumiem rozbicie 12 na iloczyn siedmiu liczb i z tego mamy trzy możliwości, lecz moc zbioru
A już niestety nie rozumiem.
Moim błędem na pewno było to, że rozróżniałem na przykład 2 i 6 i liczyłem zdarzenie za pomocą
wariancji bez powtórzeń, nadal nie rozumiem czemu to myślenie jest błędne.
Jak policzę za pomocą kombinacji to rozumiem, że wtedy wybieramy 2 elementy z 7 i nie obchodzi
 4) Nie mam pojęcia skąd ta moc zbioru A, proszę o wyjaśnienie, zależy mi na tym, żeby to
zrozumieć
4) Nie mam pojęcia skąd ta moc zbioru A, proszę o wyjaśnienie, zależy mi na tym, żeby to
zrozumieć 
 Normalnie z permutacji liczymy jakby wszystko było różne, lecz jedynki nie są i musimy
podzielić przez permutacje rozróżnialnych jedynek (które nie istnieją) i tak samo z dwójkami i
pomnożyć z jedynkami na dole tam gdzie trzeba.
Świetny pomysł.
Co do 4)
Rozumiem to tak, że mamy 6 możliwości:
1.* (1,1,1,1,x,y)
2.* (2,2,2,2,k,m)
3.* (3,3,3,3,a,b)
4.* (4,4,4,4,c,d)
5.* (5,5,5,5,g,h)
6.* (6,6,6,6,p,r)
mam 6 miejsc więc 3 możliwości ustawienia w każdym powyższym zdarzeniu:
x x x x _
xxxx_
xxxx
i liczby x,y,k,m,a,b,c,d,g,h,p,r muszą się różnić od tych w ich danym zdarzeniu.
więc mógłbym to chyba policzyć tak:
6*3*1*1*1*1*5*5
I to myślenie pewnie jest źle, nie wiem czemu
Normalnie z permutacji liczymy jakby wszystko było różne, lecz jedynki nie są i musimy
podzielić przez permutacje rozróżnialnych jedynek (które nie istnieją) i tak samo z dwójkami i
pomnożyć z jedynkami na dole tam gdzie trzeba.
Świetny pomysł.
Co do 4)
Rozumiem to tak, że mamy 6 możliwości:
1.* (1,1,1,1,x,y)
2.* (2,2,2,2,k,m)
3.* (3,3,3,3,a,b)
4.* (4,4,4,4,c,d)
5.* (5,5,5,5,g,h)
6.* (6,6,6,6,p,r)
mam 6 miejsc więc 3 możliwości ustawienia w każdym powyższym zdarzeniu:
x x x x _
xxxx_
xxxx
i liczby x,y,k,m,a,b,c,d,g,h,p,r muszą się różnić od tych w ich danym zdarzeniu.
więc mógłbym to chyba policzyć tak:
6*3*1*1*1*1*5*5
I to myślenie pewnie jest źle, nie wiem czemu  Proszę o pomoc.
Proszę o pomoc.

 Zakładałem, że jak mają być 4 pod rząd takie same to już nigdzie indziej taka sama nie może
się pojawić i to było błędne myślenie − przede wszystkim.
Dziękuję kerajs za objaśnienie zadania 3. Zrobiłem je wcześniej sam i w ten sposób, że jak
mam na przykład dla przykładu 6*2*1*1*1*1*1 mam siedem miejsc to miejsce dla 6 mogę wybrać na
Zakładałem, że jak mają być 4 pod rząd takie same to już nigdzie indziej taka sama nie może
się pojawić i to było błędne myślenie − przede wszystkim.
Dziękuję kerajs za objaśnienie zadania 3. Zrobiłem je wcześniej sam i w ten sposób, że jak
mam na przykład dla przykładu 6*2*1*1*1*1*1 mam siedem miejsc to miejsce dla 6 mogę wybrać na
 Dziękuję wam.
Co do mnie to w tym roku po raz 6. przystępuje do matury rozszerzonej z matematyki ponieważ
moim małym marzeniem jest 100%, a brakuje mi już niewiele, bo tylko 1 punkt.
Zostawiam link poniżej do postu z wglądem do mojego arkusza oraz zadania, w którym dostałem
jeden punkt mniej:
https://matematykaszkolna.pl/forum/403637.html
Jak ktoś ma jakieś przemyślenia co do mojego rozwiązania to zapraszam. Odwoływałem się do OKE,
gdzie dostałem 2% więcej za nie uznanie przez nich wyznaczenia przeze mnie największej
wartości. Z dziedziną odwoływałem się do kolegium arbitrażu egzaminacyjnego, niestety bez
skutku. Szkoda, że trzy znaki x<y tyle zmieniły.
Czuję, że to będzie w tym roku, łatwiej już nigdy nie będzie
Dziękuję wam.
Co do mnie to w tym roku po raz 6. przystępuje do matury rozszerzonej z matematyki ponieważ
moim małym marzeniem jest 100%, a brakuje mi już niewiele, bo tylko 1 punkt.
Zostawiam link poniżej do postu z wglądem do mojego arkusza oraz zadania, w którym dostałem
jeden punkt mniej:
https://matematykaszkolna.pl/forum/403637.html
Jak ktoś ma jakieś przemyślenia co do mojego rozwiązania to zapraszam. Odwoływałem się do OKE,
gdzie dostałem 2% więcej za nie uznanie przez nich wyznaczenia przeze mnie największej
wartości. Z dziedziną odwoływałem się do kolegium arbitrażu egzaminacyjnego, niestety bez
skutku. Szkoda, że trzy znaki x<y tyle zmieniły.
Czuję, że to będzie w tym roku, łatwiej już nigdy nie będzie  Materiał ze studiów chce się nauczyć, ponieważ chce go umieć i móc pomagać z nim innym:
pochodne, całki, szeregi, równania różniczkowe, płaszczyzny, funkcje dwóch, trzech zmiennych,
granice oraz płaszczyzny.
Jak to będę ogarniał to będzie super, ale oczywiście najpierw 100% z PR.
Szeregów, równań różniczkowych, funkcji trzech zmiennych w ogóle nie umiem, a płaszczyzny
bardzo słabo. Tym się na pewno zajmę w przyszłości, a niedługo chciałbym zobaczyć czy na
przykład szeregi jestem w stanie ogarnąć szybko.
Matematyka łatwo mi przychodzi i dużo zagadnień sam się nauczyłem. Więc ciągnę to dalej z
sukcesami. Lubię matematykę. Matma jest super.
Dziękuję za waszą pomoc, fajnie, że tu jesteście
Materiał ze studiów chce się nauczyć, ponieważ chce go umieć i móc pomagać z nim innym:
pochodne, całki, szeregi, równania różniczkowe, płaszczyzny, funkcje dwóch, trzech zmiennych,
granice oraz płaszczyzny.
Jak to będę ogarniał to będzie super, ale oczywiście najpierw 100% z PR.
Szeregów, równań różniczkowych, funkcji trzech zmiennych w ogóle nie umiem, a płaszczyzny
bardzo słabo. Tym się na pewno zajmę w przyszłości, a niedługo chciałbym zobaczyć czy na
przykład szeregi jestem w stanie ogarnąć szybko.
Matematyka łatwo mi przychodzi i dużo zagadnień sam się nauczyłem. Więc ciągnę to dalej z
sukcesami. Lubię matematykę. Matma jest super.
Dziękuję za waszą pomoc, fajnie, że tu jesteście 
 6. (0 – 4) Dwóch strzelców oddało po jednym strzale do tego samego celu. Oblicz
prawdopodobieństwo, że pierwszy z nich trafił, jeśli wiadomo, że cel został trafiony tylko
jeden raz. Zakładamy, że prawdopodobieństwo trafienia w cel jest równe dla pierwszego strzelca
9/10, a dla drugiego wynosi 3/4.
7. (0 – 4) Wykaż, że jeśli P(A│C) = P(A│C' ), gdzie P(C)>0 i P(C' )>0 to zdarzenia A oraz C
są niezależne.
6. (0 – 4) Dwóch strzelców oddało po jednym strzale do tego samego celu. Oblicz
prawdopodobieństwo, że pierwszy z nich trafił, jeśli wiadomo, że cel został trafiony tylko
jeden raz. Zakładamy, że prawdopodobieństwo trafienia w cel jest równe dla pierwszego strzelca
9/10, a dla drugiego wynosi 3/4.
7. (0 – 4) Wykaż, że jeśli P(A│C) = P(A│C' ), gdzie P(C)>0 i P(C' )>0 to zdarzenia A oraz C
są niezależne.
 Każda pomoc jest dobra
Każda pomoc jest dobra 

 6)
T− cel trafiony jeden raz
6)
T− cel trafiony jeden raz

 Miłe to...... .......
Miłe to...... .......

 Każde poprawne rozwiązanie uczy i daje do
myślenia
Każde poprawne rozwiązanie uczy i daje do
myślenia 

 Wypisałem takie
możliwości:
232121
232123
232321
232323
321212
321232
323212
323232
Jeśli niczego nie przeoczyłem to |A| = 8
Wypisałem takie
możliwości:
232121
232123
232321
232323
321212
321232
323212
323232
Jeśli niczego nie przeoczyłem to |A| = 8
 To jaki zapis kerajs proponujesz, żeby był on poprawny?
Już mam opłacony egzamin więc na pewno do niego podejdę
To jaki zapis kerajs proponujesz, żeby był on poprawny?
Już mam opłacony egzamin więc na pewno do niego podejdę  Trzeba jeszcze wiedzieć co chce się w życiu robić, a ja tego jeszcze raczej nadal szukam.
Ale dziękuję za przemyślenia. 100% zdobędę w tym roku i już koniec mojej przygody z maturami
Trzeba jeszcze wiedzieć co chce się w życiu robić, a ja tego jeszcze raczej nadal szukam.
Ale dziękuję za przemyślenia. 100% zdobędę w tym roku i już koniec mojej przygody z maturami 
 Nie wychodzi mi
Nie wychodzi mi 
 C − wylosowano kule czarną
C − wylosowano kule czarną



 1 zielona w urnie U4 gdy:
(b,b,z) (b,z,c) (c,b,z) (c,z,c)
2 zielone w U4 gdy:
(b,z,z) ( c,z,z)
1 zielona w urnie U4 gdy:
(b,b,z) (b,z,c) (c,b,z) (c,z,c)
2 zielone w U4 gdy:
(b,z,z) ( c,z,z)



 Jak można to tak ogarniać, też bym chciał
Jak można to tak ogarniać, też bym chciał 


