konstrukcja Qulka: nie pamiętam .... jak podzielić konstrukcyjnie obwód trójkąta na połowy

Qulka: https://www.euclidea.xyz/en/game/packs/Theta/level/PerimeterBisector

Mariusz: Właśnie zaczynam się tym bawić i np druga konstrukcja z poziomu α to część konstrukcji pierwszej Czy wcześniej nie było konstrukcji którą można by wykorzystać ?

Qulka: mam już kilka dostępnych narzędzi (w końcu się dorobiłam ruchomego cyrkla).. ale nie mam pomysłu by się zmieścić w limicie

Mariusz: Kiepsko mają zrobioną rejestrację Co wpisuję nazwę użytkownika to wypisują komunikat że "Użytkownik już istnieje" Jakiś czas temu napisałem w Pascalu programik do wypisywania pseudolosowego ciągu znaków I nawet po wpisaniu tych pseoudolosowo wygenerowanych znaków wypisują komunikat że "Użytkownik już istnieje" Bez zalogowania nie zapisują konstrukcji i dlatego odechciało mi się tej zabawy Byłem już przy ostatniej konstrukcji z poziomu zeta Czy ty nie miałaś problemu z rejestracją ?

Qulka: chyba w ogóle się nie rejestrowałam.. ale wisi u mnie nie zamykany w zakładce więc nie pamiętam.. ale chyba wcisnęłam tylko play now i już ... aha.. czyli jak zamknę to już nie wrócę... ale co się naumiem to moje

Mariusz: Odłożyłem pozostałe boki na prostej zawierającej jeden z boków i dałem symetralną Zaliczyło mi ale dostałem tylko dwie gwiazdki V oraz E

Mariusz : Qulka po zalogowaniu zapisuje wykonane konstrukcje Oprócz tworzenia nowego konta jest możliwość zalogowania przez konto na google lub na facebooku Program dobry np jak chcesz syna zachęcić do geometrii Teraz jestem przy poziomie jota Można się tam dopatrzeć twierdzenia Talesa i podobieństwa trójkątów Twierdzenie Talesa w jednym z zadań mi pomogło choć po jego zastosowaniu nie zmieściłem się w limicie Bardzo rzadko udaje mi się zmieścić w obydwu limitach Np w jednym z zadań z rysunku wynikało aby jeden kąt podzielić na dwa a następnie drugi z kątów podwoić Gdy wykonałem konstrukcję zgodnie z tymi wskazówkami to nie zmieściłem się w obydwu limitach

Qulka: doczytałam się ze niektóre zadania robi się oddzielnie na gwiazdkę L i oddzielnie na E i czasem pojawia sie gwiazdka V jak zrobisz wszystkie możliwe sposoby utknęłam na trójkącie o minimalnym obwodzie wpisanym w kąt i przez dany punkt czyli 9.1

Mariusz : Odbicie symetryczne danego punktu względem obydwu ramion kąta i prosta przechodząca przez tak powstałe punkty Czy to jest to zadanie ? Ja za to dostałem tylko gwiazdkę V Może znajdziesz jakieś lepsze rozwiązanie Tu jest też tryb z pokazanym rozwiązaniem i wszystkimi dostępnymi gotowymi konstrukcjami tzw narzędziami których użycie inkrementuje licznik L (żółty przycisk w górnym prawym rogu) Ja utknąłem za zadaniu w którym przekątne trapezu dzielą odcinek łączący jego ramiona na trzy części Widzę tu trójkąty podobne ale nic z tego podobieństwa nie da się wywnioskować

Qulka: środkowe z dwóch górnych na podstawę i przecięcie ich z przekątnymi

Mariusz: Mój pomysł polegał na skonstruowaniu takich krzywych aby przecinały się w jednym punkcie na szukanym odcinku Mając taki punkt wystarczyłoby poprowadzić prostą równoległą do jednej podstaw przechodzącą przez ten wyznaczony punkt W podobny sposób co opisałem powyżej rozwiązałem zadanie 9.3 (Tutaj przekątne przecinały się w jednym punkcie na szukanym odcinku) Jakie wiadomości z geometrii mogłyby się przydać do wyprowadzenia konstrukcji bo ja myślałem nad podobieństwem trójkątów czy twierdzeniem Talesa

Mariusz: Na pewno twoja konstrukcja jest poprawna ? Mogłabyś ją opisać dokładniej ? Może takie coś mogłoby pomóc https://prnt.sc/xz0r0k

Qulka: pisałam o tym zadaniu https://prnt.sc/xz8c7n

Qulka: a średnia harmoniczna to znalazłam że to po prostu równoległa przechodząca przez przecięcie przekątnych

Qulka: http://www.kowalskimateusz.pl/srednia-sredniej-nie-rowna/

Qulka: tu jest fajnie http://matematyka.sosnowiec.pl/teoria30a.html

a@b: https://matematykaszkolna.pl/forum/49788.html tu też

a@b: https://matematykaszkolna.pl/forum/380315.html i tu

Mariusz: Ja do konstrukcji z średnią harmoniczną to sam doszedłem ale metodą prób i błędów Choć zaliczyło mi tylko gwiazdkę L Co do 9.6 to widziałem taką konstrukcję https://prnt.sc/xzgqnv Chodziło mi o to aby uzasadnić poprawność konstrukcji korzystając ze znanych twierdzeń Na pierwszy rzut oka myślałem że koleś skorzystał z twierdzenia Talesa ale jednak nie ma tam prostych równoległych Teraz rozpocząłem poziom kappa

Mariusz: "środkowe z dwóch górnych na podstawę i przecięcie ich z przekątnymi" Gdybyś to zdanie zbudowała poprawnie nie byłoby problemu ze zrozumieniem o jakie środkowe chodziło Poprowadź środkowe dolnej podstawy z obydwu wierzchołków górnej podstawy Połącz punkty przecięcia środkowych z przekątnymi Lepiej brzmi ?

Qulka: dużo lepiej ale nie piszesz o 1 w nocy dopiero się uczę poprawności wymowy, bo zaczęłam w tym roku uczyć i muszę zacząć myśleć co mówię jak zrobiłeś ten trójkąt na ortocentrum

Mariusz: https://prnt.sc/xzljw6 Jak widzisz można tę konstrukcję wykonać w mniejszej liczbie kroków ale zaliczyć powinno

Mariusz: Postaram się opisać kroki Niech punkty A B C będą wierzchołkami trójkąta Prosta BO Okrąg o środku w B i promieniu OB Przecięcie okręgu O(B,OB) z prostą BO to punkt O' Okrąg o środku w B i promieniu OO' Punkt D to przecięcie okręgu O(B,OO') z prostą BO Prosta p równoległa do prostej AB i przechodząca przez punkt D Punkt E to przecięcie prostej p i prostej BC Symetralna BD Punkt F to przecięcie symetralnej BD i prostej BO Prosta przechodząca przez punkty E oraz F zawiera szukany odcinek

Qulka: z obrazka odczytałam ale dzięki

Mariusz: A masz jakiś pomysł na zminimalizowanie liczby kroków ?

Qulka: jak dojdę do końca będę się wracać i kombinować...może w międzyczasie się nauczę jakiś myków

Mariusz: To napiszę ci jak doszedłem do rozwiązania tego zadania z trójkątem o podanym kącie i ortocentrum Przełączyłem na tryb z pokazanym gotowym rozwiązaniem i odmierzyłem odległość od środka poszukiwanego odcinka do wierzchołka podanego kąta gdzie za jednostkę przyjąłem odległość od środka poszukiwanego odcinka do ortocentrum Gdy już znałem położenie środka poszukiwanego odcinka skorzystałem z rozwiązania zadania 7.9 które oparłem na konstrukcji równoległoboku Może to ci się później przyda jak będziesz próbować zminimalizować liczbę kroków Teraz nadal próbuję znaleźć sposób na konstrukcję tej stycznej do okręgu

Qulka: ja zrobiłam brutalnie na podstawie obrazka z jakiegoś filmiku https://prnt.sc/xzs5gg

Qulka: i poprawiłam punkty za prostą równoległą bo znalazłam obrazek z 3 kółkami o którym kiedyś wiedziałam ale zapomniałam

Qulka: a za styczną mam 4L https://prnt.sc/xzsadg

Qulka: utknęłam na cięciu odcinka na 3 tylko linijką

Mariusz: Ja doszedłem do rozwiązania ze styczną podobnie jak w przypadku średniej harmonicznej w trapezie dopiero po przespaniu się Nie wiem jaki to miało wpływ

Mariusz: Moje rozwiązanie zadania ze styczną jest właściwie takie samo

Kacper: Też spróbuję swoich sił

Mariusz: Wyprowadzanie konstrukcji jest łatwiejsze gdybyś wyprowadzał je z wykorzystaniem znanych twierdzeń geometrii Dobrze jest też wiedzieć co się w danym kroku robi Przykładowo − widziałem wiele konstrukcji wielokątów foremnych w których nie wiadomo co się dzieje w poszczególnych krokach Gdybyśmy jednak konstrukcję oparli o konstrukcję kąta przyległego do wewnętrznego albo o konstrukcję trójkąta równoramiennego to przy znajomości pewnych wartości funkcyj trygonometrycznych można wyprowadzić konstrukcję w której w każdym kroku wiadomo o co chodzi

Mariusz: A na tej stronie której fragment zeskanowałaś było pokazane jak wyznaczyć okrąg c bo jak biorę dowolny to nie wychodzi

Mariusz: Już chyba wiem z jakiego filmiku podejrzałać konstrukcję 10.2 https://prnt.sc/y05qb6 Da się ją usprawnić ?

Mariusz: Aby skonstruować okrąg c bez korzystania z kosztownego ruchomego cyrkla wystarczy skorzystać z rozwiązania zadania 6.3

Mariusz: Obrót o 60 stopni Wiem że trójkąt równoboczny ma kąty 60 stopni Czy można to wykorzystać Obrót o 90 stopni rozwiązałem bawiąc się prostopadłymi ale można to było rozwiązać w mniejszej liczbie kroków

Mariusz: Obrót o 60 stopni wykonałem kreśląc okręgi Czy w tym podziale odcinka na trzy części z 10.7 nie dałoby się wykorzystać tej konstrukcji z trapezem czyli 9.6 ?

Qulka: super pomysł.. dzięki udało się ale na 9L9E

Qulka: znalazłam książkę gdzie są same kółeczka... trochę bolą oczy jak brak kresek ale fajne https://www-users.mat.umk.pl//~sendlew/w9/konstrukcje-tylko-cyrkiel.pdf

Mariusz: 10.7 z twierdzenia Talesa pewnie by wyszło samym liniałem ale pewnie wymagałoby to więcej kroków niż dali w limicie a poza tym twierdzenia Talesa wygodniej korzystać gdy możemy kreślić też okręgi Andrzej Sendlewski prowadził wykłady gdy na tym wydziale zaocznie studiowałem

Mariusz: W tablicach Mizerskiego mam konstrukcję podziału na n równych części, na podwojenie odcinka oraz na podział odcinka na połowę samym liniałem Spróbuję je wykorzystać i jeśli się uda to napiszę w ilu krokach

Mariusz: Jednak z twierdzenia Talesa to chyba nie da rady bo jak dorysuję brakujące ramię kąta to nie będę miał prostej równoległej potrzebnej do odłożenia trzech równych odcinków

Mariusz: Nie miałem pomysłu i znalazłem na jednym z anglojęzycznych forów konstrukcję odcinka dzielącego dany odcinek w stosunku 2:1 Teraz tylko podwojenie odcinka które mam w tablicach i zaliczy choć z większą liczbą kroków niż tobie

Mariusz: Konstrukcję 10.8 można wykonać samym liniałem jako konstrukcję tego gościa https://en.wikipedia.org/wiki/Jakob_Steiner

przemysław g: Qulka tylko nikogo nie kłuj tym cyrklem

Mariusz: Co do konstrukcji z cyrklem to znalazłem książkę kolesia który udowodnił że takie konstrukcje są możliwe https://www.e-rara.ch/zut/content/titleinfo/5908911 Trochę brakuje możliwości edycji wpisów

Mariusz: Masz jakiś pomysł na 11.9 https://www.euclidea.xyz/en/game/packs/Lambda/level/APtOnCircleMaxDist

Mariusz: Znalazłem rozwiązanie na 2L 8E

Qulka: równoległa do dwusiecznej przechodząca przez środek okręgu

Mariusz: Ja też znalazłem akurat takie rozwiązanie , w pierwszej chwili nie miałem na nie pomysłu bo chciałem zmieścić się w limicie chociaż na L Z zadaniami 12.1−12.5 nie miałem większych problemów choć moje rozwiązania nie były optymalne jeśli chodzi o 12.6 to nie mogłem znaleźć rozwiązania i je podejrzałem ale tak na dobrą sprawę nie widać w tym rozwiązaniu dlaczego akurat takie kroki są wykonywane 12.7 Należy konstrukcyjnie wykreślić kąt wpisany oparty na średnicy gdzie dany jest okrąg , jego środek i dwa punkty przy czym każdy z nich należy do innej przyprostokątnej

Mariusz: Czy na 12.3 znalazłaś lepsze rozwiązanie niż te do którego ja doszedłem Poprowadziłem dwusieczne kątów trójkąta którego wierzchołkami są punkty A,B oraz C Punkt przecięcia dwusiecznych oznaczmy sobie jako D Poprowadziłem prostopadłą do prostej AD przechodzącą przez A etc Przy czym nie trzeba było prowadzić trzech dwusiecznych ani trzech prostopadłych Zastanawiam się nad 12.7 bo nie chcę na razie podglądać rozwiązania Gdybyś miała jakąś podpowiedź to możesz ją dać

Qulka: nie umiem podglądać rozwiązań utknęłam na 12.6

Mariusz: https://prnt.sc/ygcp5n Ciekawy jestem czy wiesz co tu się dzieje tzn dlaczego akurat takie kroki w tej konstrukcji zostały wykonane

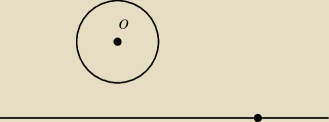
Mariusz: Masz pomysł na okrąg styczny do podanej prostej w danym punkcie i do podanego okręgu z zaznaczonym środkiem ? Jeszcze trochę się tym pobawię ale gdybyś miała jakiś pomysł ...

Qulka: prostopadła w A i dołożyć to kółko od tego punktu A i symetralną OA która przecina prostopadłą w środku szukanego kółka https://prnt.sc/yih0ju

Qulka: w 12.6 na pewno najpierw obrócili punkt 120° żeby mieć go na tej samej prostej co drugi punkt. ale dlaczego drugie przecięcie wyznacza wierzchołek to nie umiem się domyślić

Mariusz: Czy w 13.1 promień tego pomocniczo dorysowanego okręgu ma tę samą długość co promień danego okręgu ?

Qulka: tak

Mariusz: Te zadania konstrukcyjne rozwiązujesz tak na chybił trafił czy starasz się korzystać ze znanych twierdzeń Ja np zastanawiałem się jak w 13.2 wykorzystać jednokładność

Mariusz: ale raczej mało prawdopodobne jest że uda się z tej jednokładności skorzystać

Mariusz: Inną opcją mógłby być obrót o 60 stopni tylko jak się go konstruowało W jednym z zadań do obrócenia był odcinek i wystarczyło wykreślić cztery okręgi

Qulka: staram się znaleźć jakieś zależności .. nauczyć się jakiś konstrukcji (bo już od lat nic nie rysowałam) albo korzystam z Twoich podpowiedzi obrót o 60° to malujesz z kółek trójkąt równoboczny

Mariusz: Jeśli chodzi o to podejście do zadania 13.2 wykorzystujące obrót to trzeba by znaleźć punkt wokół którego należy te wierzchołki obrócić

Mariusz: Z tym obrotem też chyba nie będzie dobry pomysł bo musimy mieć środek okręgu opisanego bądź wpisanego Dla trójkąta równobocznego symetralne boków , środkowe oraz dwusieczne kątów przecinają się w jednym punkcie

Qulka: też na nim utknęłam

Mariusz: Jak coś wymyślisz tak aby dało się dość zrozumiale opisać to daj znać

Qulka: szukając jakichś symetrii i żeby było widać czy ma sens to na gotowym wyniku wyszło mi że : https://prnt.sc/yojp6e kółko o R= odległości między prostymi i środkowa prostych przecinają się w połowie podstawy. mając już symetralną boku , środkową, dwusieczną kąta i wysokość (niepotrzebne skreślić ) będzie można zoptymalizować resztę bo dzielenie na 3 albo dwusieczna 60° są kosztowne

Mariusz: Jesteś na dobrej drodze teraz prostopadła do środkowej i będziesz miała jeden z boków a dwie dodatkowe linie połączą wyznaczone wierzchołki z tym danym

Mariusz: Jak sobie z 13.3 poradziłaś ? W 13.4 jedną z opcji będzie jednokładność

Qulka: 13.3 jeszcze czeka ... chętnie się dowiem jak

Mariusz: Rozwiązanie nieoptymalne − obrót danego okręgu o mniejszym promieniu o 60 stopni wokół podanego punktu Jeden z punktów przecięcia obróconego okręgu z tym danym o większym promieniu to wierzchołek poszukiwanego trójkąta Mając podstawę trójkąta możesz dać np symetralną i wtedy przecięcie symetralnej z tym danym okręgiem o mniejszym promieniu da brakujący wierzchołek

Mariusz: Qulko przeglądałaś Geometrię Zydlera ? Może tam coś ciekawego wypatrzysz

Mariusz: W 13.5 doszedłem do czegoś takiego https://prnt.sc/ytdsmn Jeśli doszłaś do rozwiązania w mniejszej liczbie kroków to możesz się pochwalić

Mariusz: 13.6 rozwiązałem w sposób analogiczny do 11.6 a na to 13.7 z kwadratem wpisanym w okrąg nie mam pomysłu

Qulka: niedawno czytałam na forum że nauczyciel to na tyle wolnego czasu... a ja jak zaczęłam dziś o 8 to właśnie skończyłam część zdalną teraz cicha praca własna czyli ułożenie zadań na jutro i sprawdzenie dzisiejszych...znów nie ma kiedy spać konstrukcje muszą trochę poczekać

Qulka: 13.7 kółko na średnicy z punktu i analogicznego punktu pod kątem 90° https://prnt.sc/z5mgq3

Eta: Czemu nauczyciel jeszcze nie śpi ? Ja już padam Dobranoc

Qulka: a bo skoro tak wcześnie się ogarnęłam z najpilniejszą robotą to pomyślałam że może chwilkę na konstrukcję poświęcę ale też już idę słodkich snów i za banieczki mydlane

Qulka: masz 13.9

Mariusz: 13.9 https://prnt.sc/zqckz3 Może udałoby się bez tego ruchomego cyrkla

Mariusz: Prosta CD prostopadła do CD Okrąg o środku w B i promieniu CD Punkt E to przecięcie prostopadłej i okręgu Prosta AE zawiera bok kwadratu Pozostałe boki można znaleźć kreśląc prostopadłe

Qulka: odkryłam V .. jak zrobisz wszystkie możliwe konstrukcje ..czyli ten trójkąt można zrobić na 4 sposoby https://prnt.sc/102mndf