podobienstwo problem: Mam pytanie, czy trapez abcd jest podobny do trapezu abfe? z dolu dzienks

Amaz: myślę, że nie, bo mają wspólny bok AB, dlatego nie da sie określić skali podobieństwa

Kejt: chyba nie, bo mają jeden wspólny bok..

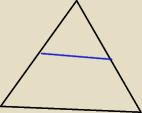
problem: A w przypadku tych dwóch trójkątów?

Amaz: tutaj istnieje prawdopodobienstwo o ile tamte odcinki są do siebie równolegle

Amaz: podobieństwo nie prawdopodobieństwo XDDD

ola: w przypadu trapezu są podobne, jeśli EF jest równoległy do DC to z własności bok, kąt,kąt są podobne , tak samo w trójkącie,

Amaz: te trapezy nie są podobne, bo nie mozna określic skali podobieństwa

ola: gdybyśmy mieli dane, np. długość odcinków moglibyśmy określić skale podobieństwa

problem: czy ktos to rozstrzygnie?

Kejt: trapezy nie są podobne.. a co do trójkątów.. rysunek nie jest zbyt dokładny..

problem: Chodzi o to, że podstawy obu figur zarówno w jednym jak i drugim przypadkku są równoległe Rysunek jest tylko szkicem

ola: bym wam to narysowała ale w tym programie nie wiele mi wychodzi figury/trójkąty są podobne w 3 przypadkach − gdy 3 boki są odpowiednoi proborcjonalne −2 boki i kąt między nimi są odpowiednio proorcjonale − 3 kąty są równe

Jack: to że "nie można określić skali podobieństwa", to o niczym nie świadczy. Na przykładzie z trójkątami też nie widać tego podobieństwa, a jednak podobne są. Swoją drogą wystarczy wziąć odpowiednie boki, podzielić ich długości i będziemy mieli podobieństwo... Niemniej te dwa trapezy nie są do sobie podobne. Gdyby były każdy bok byłby zmniejszony albo zwiększony o pewien współczynnik k. O ile jednak dolna podstawa jest zmniejszona, to górna jest ta sama w obu przypadkach. Więc na pewno te trapezy nie są podobne.

problem: ole, to o czym ty piszesz to chyba dotyczy tylko trojkatów, czworokątów już nie

Kejt: trójkąty są podobne. a z tymi kątami to trzeba uważać.. jest podobny.. znaczy, że jest przedstawiony w jakiejś skali, która dotyczy WSZYSTKICH boków. tak wiec analogicznie, nie mogą mieć wspólnej tej samej części, bo ten bok nie byłby przedstawiony w skali..

ola: dotyczy wszystkich figur,

ola: Do Jacka, skoro wszystkie odpowiadjące sobie kąty w tych trapezach są równe to te figury są podobne

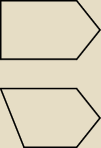
problem: Chyba jerdniak nie napisaleas : − 3 kąty są równe zobacz te dwie figury maja trzy katy równe

problem: Ok dzieki za dyskusje zgadzam sie z Jack z Tobą. pzdr.

ola: no tak, racja, te własności dotyczą trójkątów, do figur to wszystkie kąty muszą być sobie równe

Amaz: lol przeciez to było widać od razu, rzeczywiście istnieje mozliwość, zeby trapezy byly podobne, nawet jesli mają jeden bok takiej samej dlugości, ale napewno nie w tym przypadku

problem: olunia, jednak wychodzi ze dla czworokątów, kąty nie swiadczą o podobienstwie co dowodzi przyklad z trapeazamii który uswiadomil mi tą rzecz o której myslalem do dzisiaj inaczej

ola: dlaczego uwarzasz że kąty nie świadczą o podonieństwie?

ola: dobra weż 2 prostokąty, jesen o bokach 2,3 drugi o bokach 2,5 czy one są podobne?

Kejt: czy każde dwa prostokąty są do siebie podobne? ;>

ola: moim zdaniem tak

Kejt: weźmy dwa prostokąty.. powiedzmy o bokach 4x5 i 2x8 wg Ciebie one są podobne: ale: ⁴₅≠²₈ prawda?

ola: patrzysz na boki, spójrz na kąty każdy ma 90 stopni, są podobne

Kejt: jeśli są podobne, to stosunek boków powinien się zgadzać..

Kejt: https://matematykaszkolna.pl/strona/514.html

ola: racja, czyli ja jej nie mam sorry wszystkich, ale co do trójkątów to napewno się zgadza

Jack: Zgodność kątów to (niekiedy) za mało... Idea podobieństwa polega na odpowiednim stosunku boków. Dla trójkąta mamy takie zasady typu: kkk, to prawda. Natomiast dla czworokąta już nie, dobry przykładem jest właśnie prostokąt podany wyżej. Nie występuję tu jako ekspert , ale stosunek długości boków to podstawa (niekiedy dochodzi się do niej poprzez analizę kątów − jak w przypadku trójkątów. Ale praktycznie to wyjątkowy przypadek).

ola: wiem , zasugerowałam się trójkątami, z figur podobnymi to są raczej kwadrat, czy koło, okrąg

Jack: oki Na pewno każda figura foremna k−kątna jest podobna do innej foremnej k−kątnej. Inne prawidła nawet ciężko mi pomyśleć...

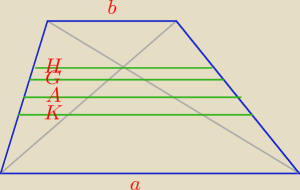
Bogdan: Jest okazja do pokazania ciekawych własności trapezu. Weźmy dwie dodatnie liczby: a, b, a ≥ b K) Średnia kwadratowa liczb a, b: s_K = √ (a² + b²)/2 .

	a + b
A) Średnia arytmetyczna liczb a, b: sA =		.
	2

G) Średnia geometryczna liczb a, b: s_G = √ab.

	2		2ab
H) Średnia harmoniczna liczb a, b: sH =		=		.
	1   1   +   a   b		a + b

Wszystkie te liczby można znaleźć w trapezie o podstawach długości: a, b. K) Długość równą średniej kwadratowej ma odcinek równoległy do podstaw trapezu i dzielący trapez na dwa trapezy o równych polach powierzchni. A) Długość równą średniej arytmetycznej ma odcinek równoległy do podstaw trapezu i łączący środki ramion trapezu. G) Długość równą średniej geometrycznej ma odcinek równoległy do podstaw trapezu i dzielący trapez na dwa trapezy podobne. H) Długość równą średniej harmonicznej ma odcinek równoległy do podstaw trapezu i przechodzący przez punkt przecięcia przekątnych trapezu. a ≥ s_K ≥ s_A ≥ s_G ≥ s_H ≥ b przy czym równości zachodzą dla a = b.

Wydi: Skąd Bogdan znasz takie informacje... zawsze mnie to ciekawiło patrząc po zadaniach które rozwiązujesz

Bogdan: To ciekawość wiedzy sprawiła

Krzychu: Tylko G dzieli trapezy na dwa podobne?