algebra Filip: Znalezc rzut prostokatny punkty P=(1,9,1) na prosta x=1+2t y=2+t z=2t Zalezc wspolrzedne rzutu prostokatnego punktu P=(2,0,1) na plaszczyzne π:x+2y−1=0

jfranek: W pierwszym pokombinuj z płaszczyzną przechodzącą przez punkt P

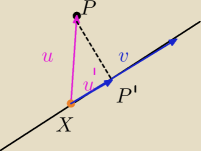
Maciess: Wybierz punkt z prostej (X). Odczytaj wektor kierunkowy prostej (v). Policz wektor XP. Zrzutuj wektor XP na v (u'). Obraz twojego punktu P to X+u'

Damian#UDM: https://matematykaszkolna.pl/forum/403768.html https://matematykaszkolna.pl/forum/65569.html Może to się Tobie przyda

Maciess: W drugim. Weź wektor nornalny płaszczyzny. Prosta X=P+t*wektor_normalny Rozwiąża układ

piotr: funkcja kwadratu odległości danej prostej od punktu P: (1+2t−1)²+(2+t−9)²+(2t−1)² osiąga min. dla t=1 ⇒ P'(3, 3, 2)

Filip: Tak, pierwsze juz policzyłem i wyszło mi tak jak tobie piotr Maciess pokazesz jak zaczac chociaz? Jakos tego nie widze

piotr: *funkcja kwadratu odległości punktu na danej prostej od punktu P:

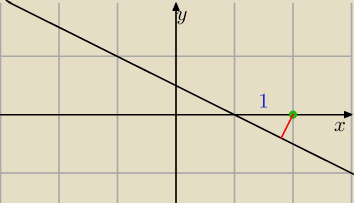
piotr: Drugie zadanie sprowadza się do obliczenia na płaszczyźnie z=0: odległość punktu (2, 0) od prostej x+2y−1=0

piotr: a rzut: z układu równań: x+2y−1=0 y=2x−4 z=1 ⇒ x = 9/5, y = −2/5, z=1

Maciess: @Filip Nie wiem czy dalej potrzebne ale wstawie Wektor normalny plaszczyny N=(1,2,0) Prosta prostopadla do tej plaszczyzny przechodząca przez punkt P ma rownanie (x,y,z)=(2,0,1)+t(1,2,0) Punkt przecięcia się tej prostej i twojej płaszczyzny to będzie rzut punktu P na tę płaszczyznę. Dostajemy układ

⎧	x=2+t
⎜	y=2t
⎨	z=1	Wyliczamy z niego t podstawiając do ostatniego rownania
⎩	x+2y−1=0

	1
t=−		Wstawiasz t do rownania parametrycznego prostej
	5

i otrzymujemy szukany rzut. Wynik wyszedl jak u kolegi wyżej.

Mila: 1) P=(1,9,1) P'=(1+2t,2+t,2t)∊prostej − rzut punktu P na prostą PP'^→=[2t,t−7,2t−1] k^→=[2,1,2]−wektor kierunkowy prostej PP'^→⊥k^→ [2t,t−7,2t−1] o [2,1,2]=0 t=1 P'=(3,3,2)