Płaszczyzny, funkcje trzech zmiennych, geometria analityczna trzech zmiennych Damian#UDM:

	x−3		y+1		z
1. Przez punkt wspólny prostej l:		=		=		i
	2		3		−1

	x−4		y+3
płaszczyzny α: 5x−3y−z−14=0 poprowadź prostą równoległą do k:		=		=
	4		3

	z−2
		.
	2

2. Oblicz objętość bryły ograniczonej przez powierzchnie: x+y=1, x−y=1, x=0, z=−2, x+y+z=3 . 3. Zbadaj wzajemne położenie płaszczyzn α: x+3y−2z−2=0 i β: x+y+2z=0 oraz płaszczyzny β i

	x		y−1		z−2
prostej l:		=		=		.
	0		−1		3

4. Oblicz objętość bryły ograniczonej przez powierzchnie: x+y=1, x−y=−1, y=0, z=−3, x+y+z=2 . Nie mam żadnego pojęcia o funkcjach trzech zmiennych, a chciałbym bardzo umieć rozwiązywać takie zadania Jeśli ktoś wie gdzie mogę znaleźć dostęp do materiałów na ich temat to byłoby super! Z góry dziękuje za każdą okazaną mi pomoc O liczeniu objętości to tyle wiem, że warto narysować to wszystko w układzie współrzędnych i wtedy powstanie jakaś bryła, np. walec ścięty lub jakaś część walca czy stożek nieskończony.

Minato: Albo zainteresuj się Geometrią analityczną (autor: Franciszek Leja) lub analizą funkcji wielu zmiennych np. (Rachunek różniczkowy i całkowy, G. M. Fichtenholz)

Mila: 1) Punkt wspólny prostej l i płaszczyzny α Parametryczne równanie prostej l: l: x=3+2t y=−1+3t z=−t, t∊R 2) Podstawiamy do równania płaszczyznyα: 5x−3y−z−14=0 5*(3+2t)−3*(−1+3t)−(−t)−14=0 t=−2 ( sprawdź) P=(3+2*(−2), −1+3*(−2), 2)⇔ P=(−1,−7,2) − szukany punkt wspólny 3) k^→=[4,3,2] wektor kierunkowy prostej k 4) Równanie prostej równoległej do k i przechodzącej przez punkt P

	x+1		y+7		z−2
m:		=		=
	4		3		2

m||k i P∊m =====================

Mila: Zadanie 3) 1) α: x+3y−2z−2=0 β: x+y+2z=0 Płaszczyzny nie są równoległe:

1
	=1
1

3
	=3≠1
1

Płaszczyzny przecinają się: 2) n₁^→[1,3,−2]− wektor normalny pł. α n₂^→=[1,1,2]−wektor normalny pł. β

	1*1+3*1+(−2)*2		0
cos(n1,n2)=		=		=0
	√12+32+(−2)2*√12+12+22		√14*√6

Płaszczyzny są prostopadłe. 3) x+3y−2z−2=0 x+y+2z=0 Przyjmuje z=t, t∊R x+3y=2t+2 x+y=−2t −−−−−−−−−−− odejmuję stronami 2y=4t+2 y=2t+1 x=−2t−(2t+1)= −4t−1 −−−−−−−−−− Płaszczyzny przecinają się, a częścią wspólną jest prosta: k: x=−4t−1 y=2t+1 z=t , t∊R 4) Wzajemne położenie pł. β i prostej l sam spróbuj

jc: 3 płaszczyzny: x+y=1, x−y=−a, y=0 są prostopadłe do płaszczyzny z=−2. Przecięcie daje trójkąt o wierzchołkach: (0,1,−2), (1,0,−2), (−1,0,−2), środku (0,1/3,−2) i polu 1. Przecięcie z płaszczyzną x+y+z=2 jest trójkątem o wierzchołkach: (0,1,1), (1,0,1), (−1,0,3). Środek = (0, 1/3, 1/5). Odległość pomiędzy środkami = 1/5+2=11/5. Objętość bryły = 11/5.

jc: oczywiście: ... =−1 zamiast ...=a

Damian#UDM: O ludzie, ile informacji Postaram się spróbować, dziękuję wam za pomoc!

Mila:

Damian#UDM: Zadanie:

	x+3		y−1		x−2
Przez punkt wspólny prostej		=		=		i płaszczyzny α,
	1		2		−1

α: x + 2y +3z + 1 = 0 poprowadź prostą prostopadłą do α. Mam pytanie do tego zadania Obliczyłem cudem punkt wspólny jak Mila wyżej i wyszedł mi P = (−4, −3, 3) I nie wiem jak wyznaczyć prostą prostopadłą do płaszczyzny α Proszę o pomoc, niekoniecznie rozwiązanie, lecz podpowiedzenie jak się za to zabrać!

Jerzy: Wektorem kierunkowym szukanej prostej jest wektor normalny zadanej płaszczyzny, a prosta musi przechodzić przez wyznaczony punkt

Mila: Cześć Jerzy (już niebieski?)

Jerzy: Witaj Milu . Tak już odzyskał kolor

Mila: Damian jeszcze raz licz wsp. punktu wspólnego, ja mam inny wynik. Sprawdź, czy Twoje wsp. spełniają obydwa równania.

Damian#UDM: Tak, był błąd Nieszczęsny minus zamiast + Teraz punkt wyszedł mi P=(−6, − 5, 5)

Damian#UDM: Czy wektor normalny płaszczyzny to v=[1, 2, 3]?

Jerzy: Tak.

Damian#UDM: O ludzie, nie myślałem, że to będzie takie proste Bardzo dziękuję, spróbuję rozwiązać

Mila: Punkt prawidłowy

Damian#UDM: Czy ta prosta i prostopadła do płaszczyzny α jest opisana równaniem

	x+6		y+2		z−3
K:		=		=		=0
	1		2		3

?

Damian#UDM: Dziękuję Milu

Jerzy: Skup się.Twoja prosta przebija płaszcznę w punkcie: A (−6,−2,3)

Damian#UDM: Czyli jest źle? No to nie mam pojęcia jak to zrobić. Jedyne informacje na temat płaszczyzn jakie mam to te od was kochani

Jerzy: No i podaruj sobie końcówkę .... = 0

Jerzy: Wygoogluj :”równanie parametryczne prostej w R3”

Damian#UDM: Racja, to =0 przy prostej niepotrzebne

Damian#UDM: A dziękuję, dużo materiałów wyskoczyło Postaram się ogarnąć

Mila: P=(−6,−5,5) Równanie prostej:

x+6		y+5		z−5
	=		=
1		2		3

Damian#UDM: No tak, musiałem coś po prostu pomylić Pomyliłem Punkt z wektorem Dziękuję wam za pomoc!

Damian#UDM: Kiedy prosta jest równoległa do płaszczyzny?

Damian#UDM: Zadanie : Przez punkt P=(−3, 4, 2) poprowadź prostą m równoległą do prostej l,

	x−3		y+6		z−3
l:		=		=
	−1		1		−2

Oblicz odległość pomiędzy prostymi l i m. Sprawdź czy prostą m jest równoległa do płaszczyzny π: x + 2y − 3z − 2 = 0.

Damian#UDM:

	x+3		y−4		z−2
Prosta m :		=		=
	−1		1		−2

Proste są równoległe, gdy mają taki sam wektor normalny Czyli v=[−1, 1, − 2] Odległość prostych pewnie da się ze wzoru policzyć , a interesuje mnie kiedy prosta i płaszczyzna są równoległe?

Jerzy: Prosta jest równoległa do płaszczyzny,gdy jej wektor kierunkowy jest prostopadły do wektora normalnego tej płaszczyzny.

Damian#UDM: A wektory są prostopadłe, gdy ich iloczyn skalarny jest równy 0 Spróbuję to zrobić!

Jerzy: Tak.

Damian#UDM: Wektor płaszczyzny π w_π = [1,2,−3] Wektor prostej m v_m = [−1,1,−2] Vow= [−1,1,−2]o[1,2,−3]= (−1)*1+1*2+(−2)*(−3)=−1+2+6=7≠0 Zatem prosta m nie jest równoległa do płaszczyzny π

Jerzy: Nie jest.

Damian#UDM: Żeby obliczyć odległość prostej m od prostej l to muszę znaleźć płaszczyznę, która zawiera prostą l. Jak to zrobić? Proszę o pomoc! Myślę już nad tym kilka godzin i nie mam pojęcia jak

Jerzy: Jedna z metod: Rozpinamy równelogłościan na trzech wektorach ( dwa to wektory kierunkowe zadanych prostych,a trzeci to wektor o końcach w dwóch dowolnych punktach tych prostych ). Liczymy jego objętość i dzielimy ją, przez pole podstawy ( równoległobok rozpięty na wektorach kierunkowych tych prostych).Otrzymana wartość,to wysokość tego równoległościanu, czyli odległość tych prostych.

Jerzy: Oczywiście jeśli te proste leżą w jednej płaszczyźnie, to objętość wyniesie 0.

Damian#UDM: A jeśli proste są równoległe to oznacza, że leżą w jednej płaszczyźnie?

Damian#UDM: Z moich informacji wynika, że tak P_l = (−4,−5,1) P_m = (0,7,−4) Wektor P_lP_m = [4,12,−5] Wektor prostej m = wektor prostej l = [−1,1,2]

Damian#UDM: Zadanie : Obliczyć odległość punktu P=(−3,4,2) od prostej l,

	x−3		y+6		z−3
l:		=		=
	−1		1		−2

Z odległością nadal nie wiem jak to rozwiązać. Proszę o pomoc

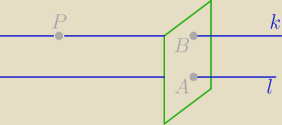
Des: 1) Znajdujesz dowolny punkt na prostej l (niech to będzie pkt A) 2) Punkt A i wektor kierunkowy prostej l pozwolą wyznaczyć płaszczyznę prostopadłą do prostej l 3) Znając punkt P i wektor kierunkowy prostej l wyznaczasz prostą k, która również jest prostopadła do płaszczyzny 4) Mając prostą k i płaszczyznę, rozwiązujesz układ równań, który da Ci punkt B 5) Odległość punktu P od prostej l to nic innego jak długość wektora AB^→

Jerzy: 1) Równanie płaszczyzny prostopadłej do prostej i przechodzącej przez P 2) Punkt przebicia prostej i płaszczyzny (B) 3) Odegłość punktów P i B

Damian#UDM: Super, dziękuje wam za pomoc Zrobiłem jak na razie sposobem Des: 1) Punkt A, A∊l dla x=1: A=(1, −4, −1) 2) Płaszczyzna α prostopadła do prostej l i przechodząca przez punkt A, α: −x+y−2x+3=0

	x+3		y−4		z−2
3) Prosta k||l i przechodząca przez punkt P, k:		=		=
	−1		1		−2

4) Punkt B, B=(−1¹₃, 2¹₃, 5¹₃) 5) Odległość punktu P od prostej l, czyli długość wektora AB, wektor AB=[−2¹₃, 6¹₃, 6¹₃], długość wektora AB = ^√771₃

Damian#UDM: W płaszczyźnie oczywiście zamiast −2x to −2z.

Jerzy: A po co wprowadzać dodatkowy punkt A. Mamy już punkt P i on wystarczy do napisania równania płaszczyny.

Damian#UDM: Już próbuję Jerzy

Jerzy: Co więcej,niepotrzebne jest wprowadzanie dodatkowych dwóch punktów.To tak jak gdyby jechać z Warszawy do Zakopanego przez Gdańsk.

Damian#UDM: Punkt przebicia prostej l i płaszczyzny to jest ich punkt wspólny różny od P?

Jerzy: Tak i pozostaje policzyć odległość tego punktu od punktu P i koniec zadania.

Damian#UDM: Sposobem Jerzy wyszło mi tak: 1) płaszczyzna β prostopadła do prostej l i przechodząca przez punkt P, β: −x+y−2z−3=0 2) Punkt B wspólny prostej l i płaszczyzny β, B=(0, −3, −3) 3) Wektor BP = [−3, 7, 5] 4) Długość wektora |BP| = √83

Damian#UDM: Super, dziękuje za pomoc Widzę, że odległość sposobem Des to w przybliżeniu 9,25, a sposobem Jerzy 9,11 , więc przypuszczam, że gdzieś mogłem popełnić błąd lub coś się nie zgadza Tak czy siak dziękuje za pomoc, teraz już wiem o wiele więcej, cieszę się, że da się nauczyć takich zagadnień bez uczęszczania na studia

jc: wektor kierunkowy prostej = v = (−1,1,−2) punkt na prostej A = (3, −6, 3) P = (−3,4,2) P−A=(−6, 10, −1) odl. = (pole równoległoboku)/(długość podstawy) = |(P−A)xv|/|v| = √83

Damian#UDM: Zadanie: Oblicz objętość zbioru ograniczonego powierzchniami z = x² + y² , x = 0 , y = 0 , z = 0 , x + y = 2 A jak zabrać się za takie zadanie?

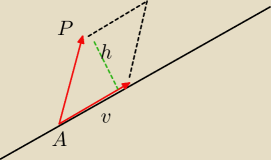
jc: Rysunek powinien wyjaśnić wszystko.

Damian#UDM: jc rozumiem, działania na wektorach, dziękuję

jc: Obszar powyżej trójkąta i poniżej paraboloidy. Liczysz całkę ∫₀² dx ∫₀^2−x (x²+y²) dy = ...

Damian#UDM: Wracając do postu 27 wrz 11:53, sposób Des jest również jak najbardziej poprawny. Zrobiłem błąd przy obliczeniach parametru s, s∊R punktu B wspólnego prostej k i płaszczyzny α. B_s = (−s−3, s+4, 2−2s), najpierw błędnie obliczyłem s=⁻⁵₃, a powinno wyjść s=−1 . Wtedy punkt B=(−2, 3, 4), oraz wektor AB = [−3, 7, 5] Zatem długość wektora |AB| = √9+49+25 = √83 . Dziękuje wam za pomoc!

Jerzy: Nikt nie twierdzi,że jest niepoprawny,ale niepotrzebnie rozbudowany.

Damian#UDM: Jasne, rozumiem o co chodzi, chciałem tylko siebie poprawić Mam pytanie do zadania z 27 wrz 12:28 Jak narysować w układzie współrzędnych x, y, z obiekt −> z = x² + y² ? Resztę równań udało mi się w nim umieścić, lecz niestety akurat tego nie potrafię

ICSP: jc podał Ci nazwę tej krzywy. Wpisz w google i zobacz jak ona wygląda. Rysowanie w 3D jest dużo trudniejsze niż w 2D

Damian#UDM: ICSP Znalazłem, dziękuje wam (jc również) za pomoc Wracając do postu Mili z 18 wrz 20:34:

	x		y−1		z−2
Wzajemne położenie płaszczyzny β: x+y+2z=0 i prostej l:		=		=
	0		−1		3

wektor kierunkowy płaszczyzny β, v_β = [1, 1, 2], wektor kierunkowy prostej l, v_l = [0, −1, 3]

1
	≠1
0

1
	≠1
−1

2
	≠1,
3

zatem prosta l nie jest prostopadła do płaszczyzny β. v_β o v_l = [1, 1, 2] o [0, −1, 3] = 1*0 + 1*(−1) + 2*3 = 0 − 1 + 6 = 5 ≠ 0, zatem prosta l nie jest równoległa do płaszczyzny β. Z tego wynika, że prosta l ma dokładnie jeden punkt wspólny z płaszczyzną β. Czy dobrze przeprowadziłem rozwiązanie zadania?

Damian#UDM: Zadanie 4. z 17 wrz 18:59 Oblicz objętość bryły ograniczonej powierzchniami: x+y=1, x−y=−1. y=0, z=−3, x+y+z=2 Przeprowadzam takie samo rozumowanie jak jc z 18 wrz 20:42 płaszczyzny x+y=1, x−y=−1, y=0, są prostopadłe do płaszczyzny z=−3. Przecięcie tych płaszczyzn daje nam trójkąt o wierzchołkach w punktach: A=(1, 0, −3), B=(−1,0,−3), C=(0, 1, −3), o środku w punkcie S_ABC=(0, ¹₃, −3), i polu równym 1. Zauważyłem, że jeśli w punktach mam taką samą współrzędną z, to mogę pole trójkąta policzyć ze wzoru z tablic matematycznych na pole trójkąta o wierzchołkach w punktach A=(x_A, y_A), B=(x_B, y_B) oraz C=(x_C, y_C) Mogę tak zrobić, ponieważ, te trzy punkty A, B, C należą do jednej płaszczyzny z=−3. Przeprowadzam dalej takie samo rozumowanie: Przecięcie płaszczyzn x+y=1, x−y=−1, y=0 z płaszczyzną x+y+z=2 daje trójkąt o wierzchołkach w punktach: D=(1, 0, 1), E=(−1, 0, 3), F=(0, 1, 1), o środku w punkcie S_DEF=(0, ¹₃, ⁵₃), czy ten środek trójkąta jest jego środkiem ciężkości ? Z drugiej strony, jeśli tutaj policzę pole trójkąta DEF z tego samego wzoru to również jest one równe 1, lecz współrzędna z tylko w dwóch punktach jest taka sama(równa 1), natomiast w punkcie E jest równa 3. Zatem nie wiem czy mogę tak robić, czy jednak są przypadki, kiedy mogę tak postąpić. Środki trójkątów mają takie same współrzędne x i y, różnią się tylko współrzędne z i z ich sumy obliczam wysokość mojej bryły: z_SABC + z_SDEF = ⁵₃ + 3 = ¹⁴₃ = 4²₃. Czy powstała bryła to graniastosłup prosty o podstawie trójkąta? Objętość liczę ze wzoru V = P_p * H, gdzie P_p − pole podstawy danej bryły, a H − wysokość danej bryły, zatem V = 1*¹⁴₃ = 4²₃

Damian#UDM: Dzień dobry wszystkim Potrzebuję waszej pomocy w rozwiązaniu poniższych zadań! 1. Wyznacz odległości L₁ i L₂ nie korzystając z gotowego wzoru na odległość od prostej. Sporządź czytelny rysunek prezentujący faktyczny przebieg prostych oraz rozwiązanie L₁ : y = 12x − 11

	⎧	x=5+2t
L2 :	⎩	y=6+24t

2. Wyznacz odległość punktu A = (8,7,9) od prostej L₃ . Podczas rozwiązania nie należy korzystać z gotowych wzorów na odległość punktów od prostej czy punktu od płaszczyzny. Sporządź szkic prezentujący sposób rozwiązania.

	⎧	x=5−2t
L3 :	⎨	y=6+6t
	⎩	z=5+0t

3. Wyznacz równanie płaszczyzny przechodzącej przez punkty B=(2,2,1), C=(7,5,0) oraz równoległej do prostej L₄ . Sporządź szkic prezentujący sposób rozwiązania.

	x−5		y−6		z−6
L4 :		=		=
	6		5		6

Sprawdzałem i zadania są dobrze przepisane Z góry dziękuję za każdą okazaną mi pomoc!