Jak używać wektorów? Wykazywanie. Szukacz: Cześć, czy mógłby mi ktoś wyjasśnićnastępujące zadania: 1. Dane są punkty: A(0,−3), B(4,−1), C(5,3), D(−3,−1). Korzystając z własności wektorów wykaż, że czworokąt ABCD jest trapezem. 2. Wykres funkcji f(x)=−2x² przesunięto równolegle o wektor v = [1,4] i otrzymano wykres funkcji g. Wykaż, że g(x)= −2x² + 4x + 2.

wredulus_pospolitus: Sprawdź czy wektor AB jest równoległy do CD (ewentualnie AD równoległy do BC)

wredulus_pospolitus: A żeby to zrobić to: a) czy wiesz jak stworzyć wektor mając współrzędne dwóch punktów? b) kiedy dwa wektory są równoległe

wredulus_pospolitus: 2. g(x) = −2x² + 4x + 2 = −2x² + 4x − 2 + 4 = −2(x² − 2x + 1) + 4 = −2(x−1)² + 4

a7: https://matematykaszkolna.pl/strona/3423.html

Mila: f(x)=−2x² v=[1,4] h(x)=f(x−1)+4 − wzór funkcji po przesunięciu o wektor [1,4] h(x)=−2*(x−1)²+4 h(x)=−2*(x²−2x+1)+4= −2x²+4x+2=g(x)

a7: https://matematykaszkolna.pl/forum/239988.html

a7: zły link wkleiłam, sorki,

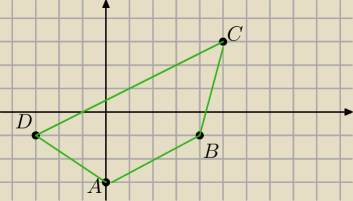
a7: robimy rysunek pomocniczy i sprawdzamy czy wektory AB^→ i DC^→ są równoległe wektor AB=a^→=[x_B−x_A, y_B−y_A]=[4−0, −1−(−3)]=[4,2] jego długość to |a^→|=√20=2√5 wektor DC=b^→=[5−(−3), 3−(−1)]=[8,4] jego długość to |b^→|=√80=4√5 sprawdzamy kąt między wektorami licząc liczy skalarny i wstawiając do wzoru na kąt między wektorami https://matematykaszkolna.pl/strona/1630.html a^→ob^→=4*8+2*4=40

	40
cosα=		=1 a więc są to wektory równoległe.
	40

Mila: wektory: [4,2], [8,4] są równoległe ponieważ :

4		2		1
	=		=
8		4		2

albo tak: 4*4−8*2=0

a7: ale skąd to bierzemy ten jakby wzór?

a7: to mój sposób jest niepotrzebnie naokoło

Szukacz: Ok, dzięki! Myślę, że mniej więcej ogarnąłem