równanie trygonometryczne salamandra: Rozwiąż równanie 3sinxtgx=2√3sinx+3cosx

	sinx
3sinx*		=2√3sinx+3cosx
	cosx

	sin2x
3		=2√3sinx+3cosx / * cosx
	cosx

3sin²x=2√3sinx*cosx+3cos²x 3sin²x−3cos²x−2√3sinxcosx=0 3(sin²x−cos²x)−2√3sin2x=0

	2√3sin2x
3(−cos2x)−		=0
	2

−3cos2x−√3sin2x=0 3cos2x+√3sin2x=0 jak mogę to dalej pociągnąć?

ICSP: podzielić przez cos2x Oczywiście przy stosownych założeniach

salamandra: no przecież... dzieki

Eta: Można też tak: ze względu na tgx , cosx≠0 dzielimy równanie obustronnie przez cosx otrzymując: 3tg²x=2√3tgx+3 a dalej już ................ ( i po ptokach

ICSP: ale −1 pkt za brak dziedziny.

Eta: Przecież napisałam na początku !

salamandra: założmy, że aż takie pomysły zachowuję na maturę

Eta:

Mila:

	π
1) x≠		założenie w wyjściowym równaniu.
	2

2)

	π
Sprawdź, czy równanie jest spełnione dla x=
	4

jeżeli nie to podziel obie strony przez cos(2x) 3) Najlepiej od razu podzielić wyjściowe równanie przez cosx, bo masz założenie j.w.

Mila: Zdublowałam

Eta: Tylko dla maturzystów ! ! (salamandra i inni matura próbna W trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego ma długość h a długość dwusiecznej kąta prostego zawartej w tym trójkącie ma długość d Wyznacz długość przeciwprostokątnej . Powodzenia

Mila: ICSP , zastosuj Twoje ciekawe przekształcenia do nierówności 402313

Eta: @ salamandra żyjesz ?

salamandra: miałem problem z zadaniem z ciągów, dopiero teraz próbuję Twoje zrobić

Eta: ok ja mam dużo czasu do matury − więc poczekam

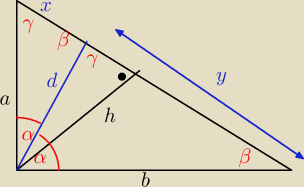
salamandra: nie wiem cyz z tego cos idzie już?

Eta: Na maturze kogo o to zapytasz? Myśl dalej ..........

fil:

	2d2h
czy odp to		?
	4d2−h2

salamandra: powiem, że mam koronawirusa i muszę na chwilę do łazienki

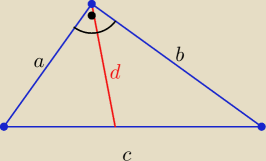
Eta: A czemu tak nie rysujesz ? ( bo na Twoim .....kark sobie skręcisz

Eta: @fil dokładnie tak

Eta: Halo, halo w mianowniku zamiast 4 jest 2

fil:

	2d2h
Po poprawce wyszlo −		, gdzies ten minus mi sie wkradl
	2d2−h2

Eta: @fil Ejj źle spojrzałam

	2d2h
c=
	2h2−d2

chyba,że źle przepisałeś

fil: Pogubilem sie w znakach, teraz wyszlo poprawnie

Eta:

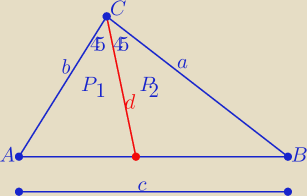
Eta: Podaję rozwiązanie ( może się komuś przyda z porównania pól ab=ch

	√2ab
d=		−−− łatwo można wykazać ( porównując P=P1+P2)
	a+b

	√2ch		2c2h2
to a+b=		|2 ⇒c2+2ab=		i a2+b2=c2 i ab=ch
	d		d2

c²d²=2c²h²−2chd² |: c ⇒ 2ch²−cd²=2hd² ⇒c(2h²−d²)=2hd²

	2hd2
c=
	2h2−d2

=============

Chorus :

	√2ab
czy można wiedzieć skąd się wzięło d=		? Mimo że matura tuż tuż kompletnie
	a+b

nie mogę tego skojarzyć

ICSP: Można. Wynika to z porównania pól P = P₁ + P₂

ICSP: https://matematykaszkolna.pl/forum/402259.html

Chorus : Dziękuję!

Eta: