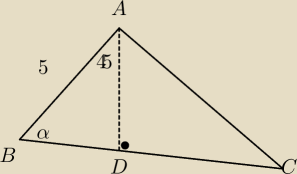
geometria analityczna salamandra: Dany jest trójkąt ABC o wierzchołkach A(−4,−1) B=(−7,−5) C=(4,−7). Oblicz długość odcinka AD dwusiecznej kąta przy wierzchołku A.

	1
PΔ=		*|(xb−xa)(yc−ya)−(yb−ya)(xc−xa)|=25
	2

AB=5 AC=10 BC=5√5 Jest to trójkąt prostokątny.

	1		2√5
PΔ na inny sposób:		*5*5√5*sinα ⇒ sinα=		, bo α − ostry.
	2		5

	√5
cosα=
	5

sin kąta ADB= sin(180−45−α)=sin(135−α)=sin135*cosα−cos135*sinα=

√2

√5

√2

2√5

√10

2√10

3√10

=

*

−(−

)*

=

+

=

2

5

2

5

10

10

10

	AD		5		10√2
z tw. sinusów:		=		⇒ AD=
	2√5   5		3√10   10		3

Tutaj to aż sam nie wiem co ja wymyśliłem, proszę o podpowiedź, bo zakładam, że to jest źle

jaros: Salamandra ty dzień w dzień ciśniesz matme od pół roku?

salamandra: Nie przesadzajmy, że dzień w dzień, powinienem robić jej więcej, ale różnie z motywacją bywało....

ICSP:

1		1
	5 * |AD| * sin45 +		10 * |AD| * sin45 = 25
2		2

5√2		10√2
	|AD| +		|AD| = 25
4		4

15√2|AD| = 100

	100		10√2
|AD| =		=
	15√2		3

Znów dobry wynik.

salamandra: No to cud nie myślałem, że z takich dziwacznych sposobów coś wykombinuję dzięki

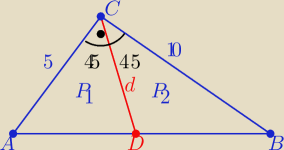
Eta: Wynik ok Można też tak: 1/ trójkąt prostokątny 5,10,5√5

	1		1
P= 25 P1=		*5*d* sin45o , P2=		*10*d*sin45o
	2		2

P₁+P₂= P ..............................

	10√2
d=
	3

==========

salamandra:

Eta: Trójkąt miał być : BCA ∡A=90^o