dowód salamandra: Wykaż, że dla dowolnej liczby rzeczywistej x spełniona jest nierówność

1		1
	x4+		x3>3x2−16
4		3

	1		1
f(x)=		x4+		x3−3x2+16
	4		3

f'(x)=x³+x²−6x f'(x)=0 ⇔ x³+x²−6x=0 x=0 v x=−3 = x=2

	1
min dla x=−3, f(−3)=
	4

max dla x=0, f(0)=16

	32
min dla x=2, f(2)=
	3

	1		1
lim (		x4+		x3−3x2+16)=+∞
	4		3

x−>+∞

	1		1
lim (		x4+		x3−3x2+16)=+∞
	4		3

x−>−∞ Czy taki dowód by przeszedł?

Eta: Narysuj jeszcze wykres pochodnej ( do uzasadnienia tych ekstremów)

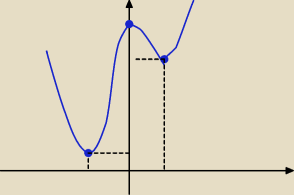
Eta: I możesz doszkicować wykres f(x)

salamandra: Nie chciało mi się tutaj rysować, na arkuszu narysowałem tak w ogóle, tutaj nie zdarzyła się taka sytuacja, ale jak szukać podzielnika współczynnika stojącego przy najwyższej potędze,

	1
jeśli jest nim np tak jak tu:		?
	4

Mariusz: Myślę że można by pomnożyć równanie bądź nierówność przez wspólny czynnik (tutaj 12) aby mieć całkowite współczynniki albo

1		1
	x4+		x3−3x2+16>0
4		3

x=6t

1		1
	1296t4+		216t3−108t2+16>0
4		3

324t⁴+72t³−108t²+16>0 Jeśli chodzi o sposób rozwiązywania równań do czwartego stopnia włącznie to widziałeś ten pdf http://matwbn.icm.edu.pl/ksiazki/mon/mon11/mon1110.pdf